SẢN PHẨM NỔI BẬT
Masteri Centre Point
TỔNG QUAN
Khu phức hợp căn hộ Masteri Centre Point với sứ mệnh nhằm mang lại cho người dân Việt Nam cuộc sống mới cao cấp không đâu sánh bằng, hội tụ đầy đủ tiện ích sang trọng trong một Thành phố sinh thái hiện đại khép kín chuẩn quốc tế giữa lòng Đại đô thị Vinhomes Grand Park đẳng cấp số 1 TP.HCM.

Mỗi căn hộ tại Masterise Homes Quận 9 – Tp.Thủ Đức được thiết kế “đo ni đóng giày” tỉ mỉ phong cách sống hiện đại, đầy đủ tiện nghi, tối ưu mọi diện tích Các thiết bị nội thất được chọn dựa trên những thiết kế hiện đại và theo xu hướng chung của Thế giới, đó là – Kohler (Mỹ) – Hafele (Đức) – Daikin (Nhật).
 |
Chủ đầu tư: Masterise Homes – Thành viên tập đoàn Masterise Group Tên dự án: Masteri Centre Point - Lumiere Boulevard Địa chỉ: Trung tâm đô thị Vinhomes Grand Park, P.Long Thạnh Mỹ, TP.Thủ Đức, TP.Hồ Chí Minh Thiết kế, kiến trúc bởi: Tange Associates – Nhật Bản, studio HBA (Mỹ), Land Sculptor (Thái Lan), Mace (Anh) Diện tích Masteri Centre Point: 70.783 m2 Quy mô dự án: Hai phân khu Centre Point và Lumiere Boulevard. Loại hình sản phẩm: Căn hộ, Duplex sân vườn, Shophouse, Penthouse. Quy mô : 5.094 căn hộ view sông – Gồm 10 tháp cao 22 đến 39 tầng. Tiện ích: Hệ sinh thái Vingroup, công viên 36 ha… Sở hữu: Lâu dài với người Việt, 50 năm cho người nước ngoài. |
VỊ TRÍ
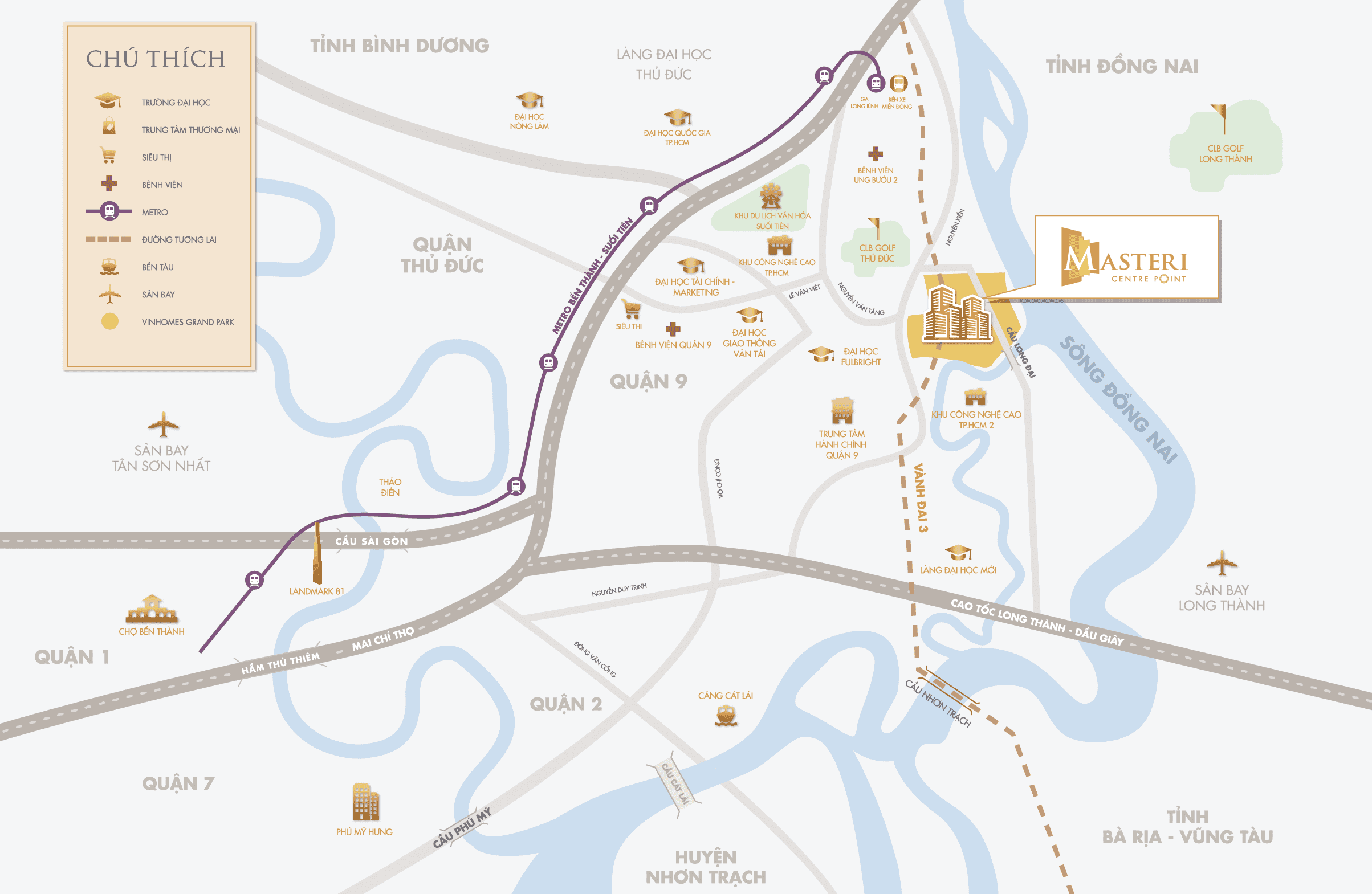
Sở hữu vị trí trung tâm Vinhomes Grand Park, Masteri Centre Point mang đến đặc quyền di chuyển nhanh vượt trội đến hệ thống tiện ích toàn diện, góp phần nâng cao chất lượng cuộc sống cho cư dân

TIỆN ÍCH

Chủ đầu tư dành hơn 50% diện tích Masteri Centre Point xây dựng tiện ích và mảng xanh.
Hệ thống tiện ích được đầu tư vô cùng bài bản, quy mô tầm cở bậc nhất Tp.HCM, mang đến giá trị sống đỉnh cao
 |
 |
 |
 |
 |
 |
 |
 |
 |
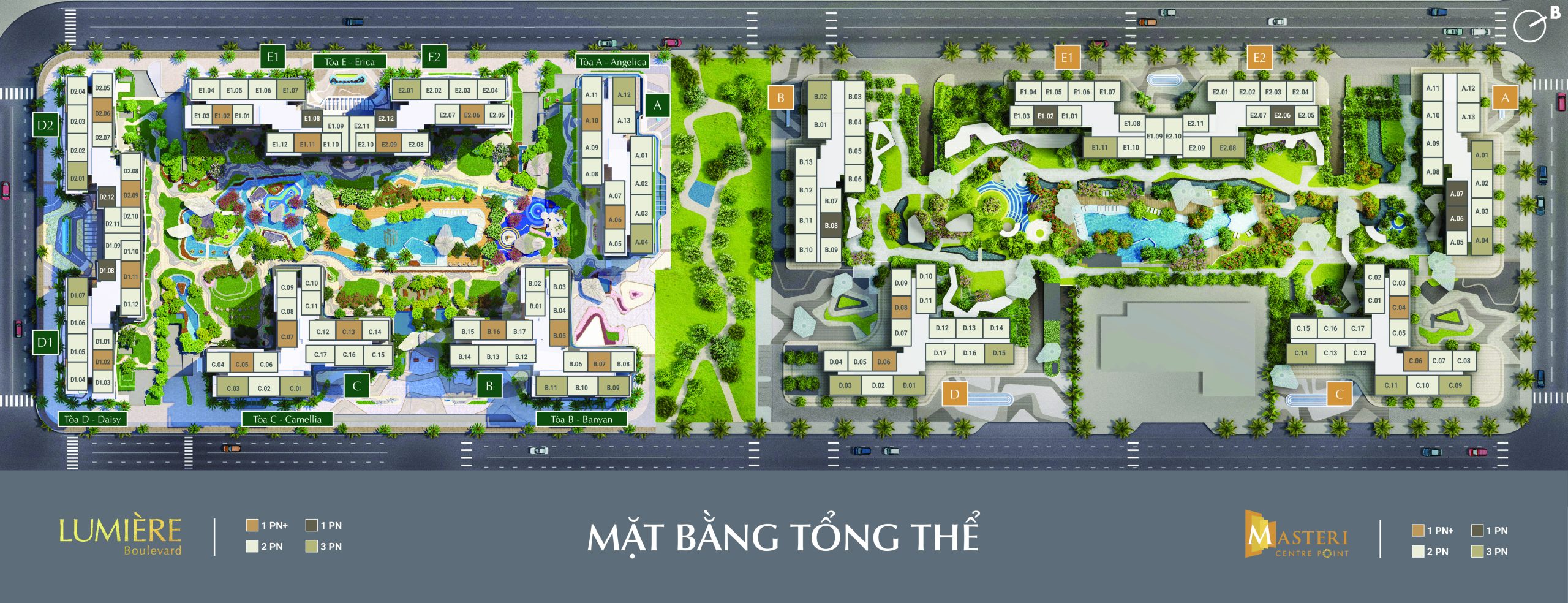
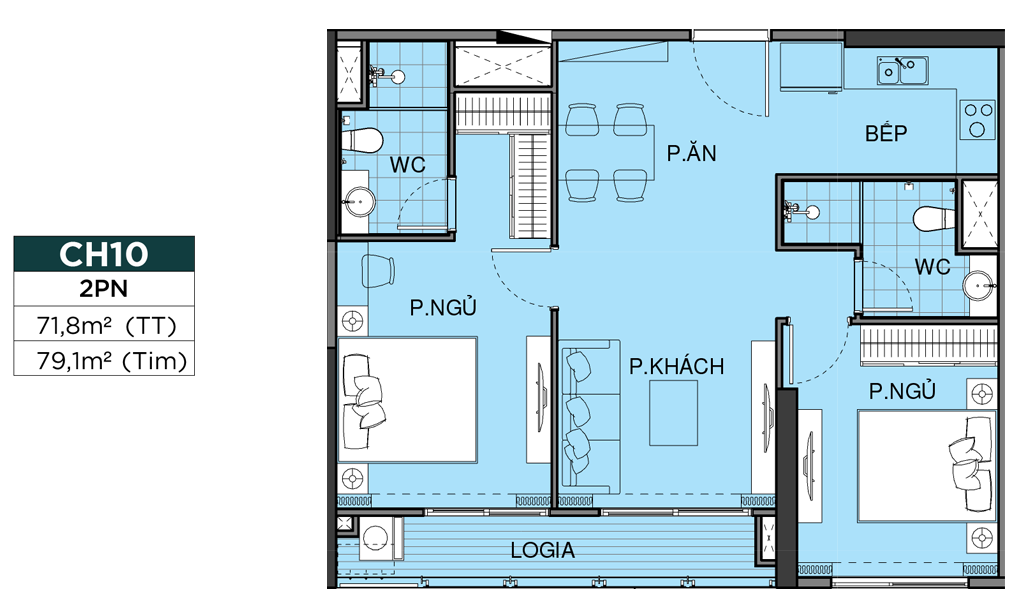
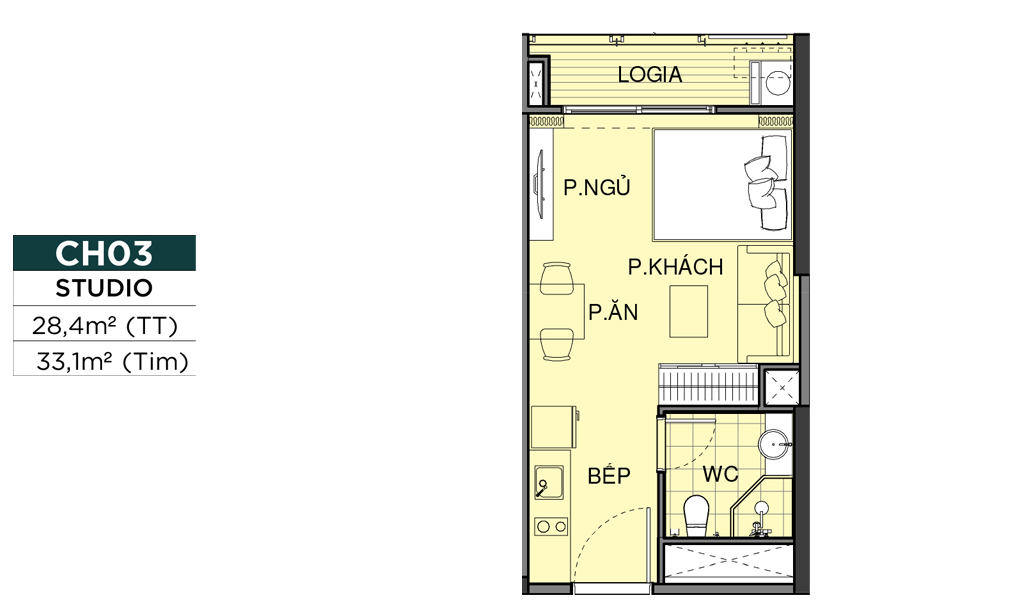
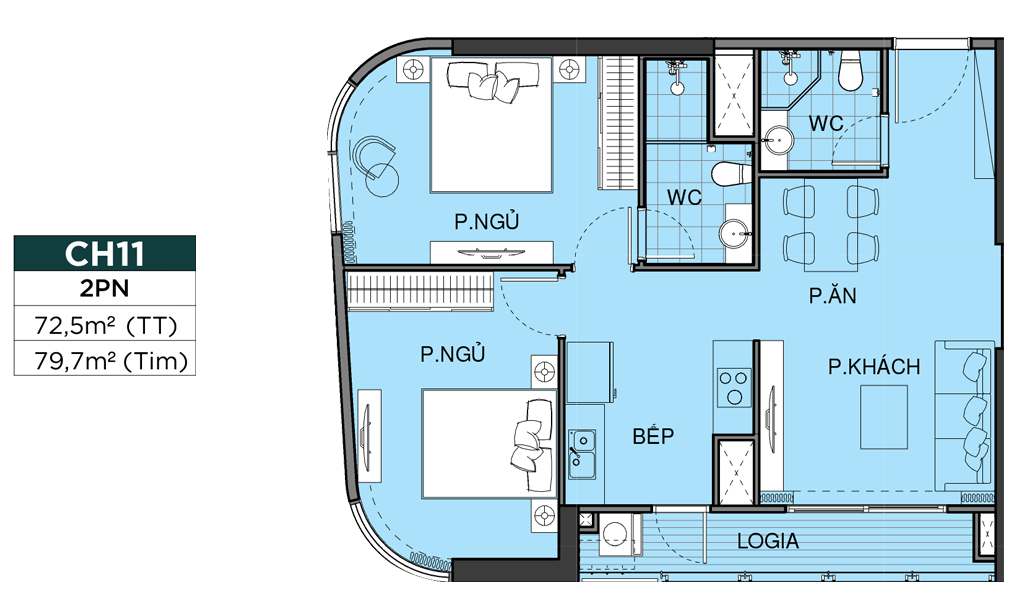
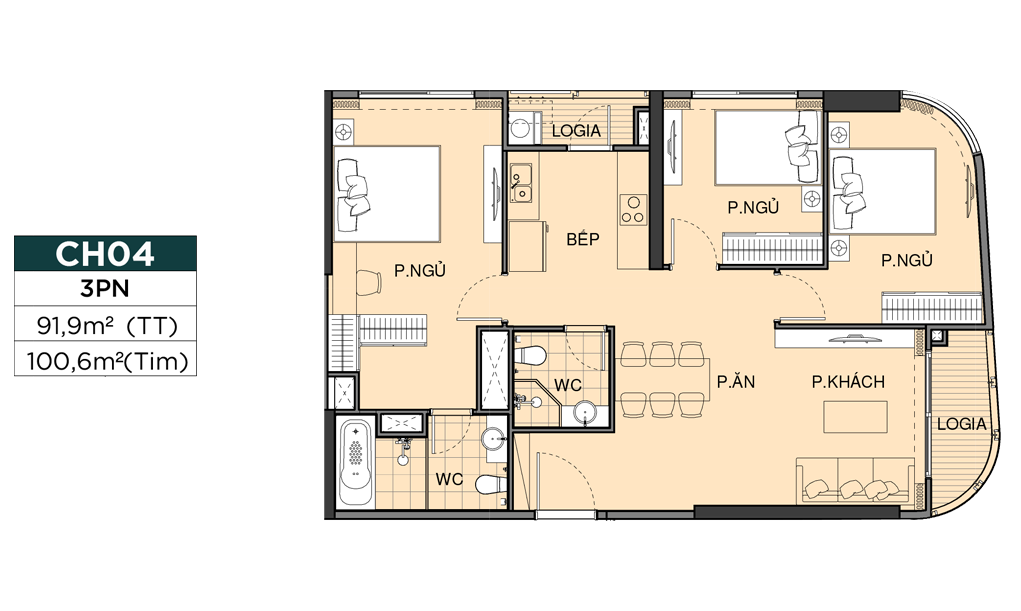
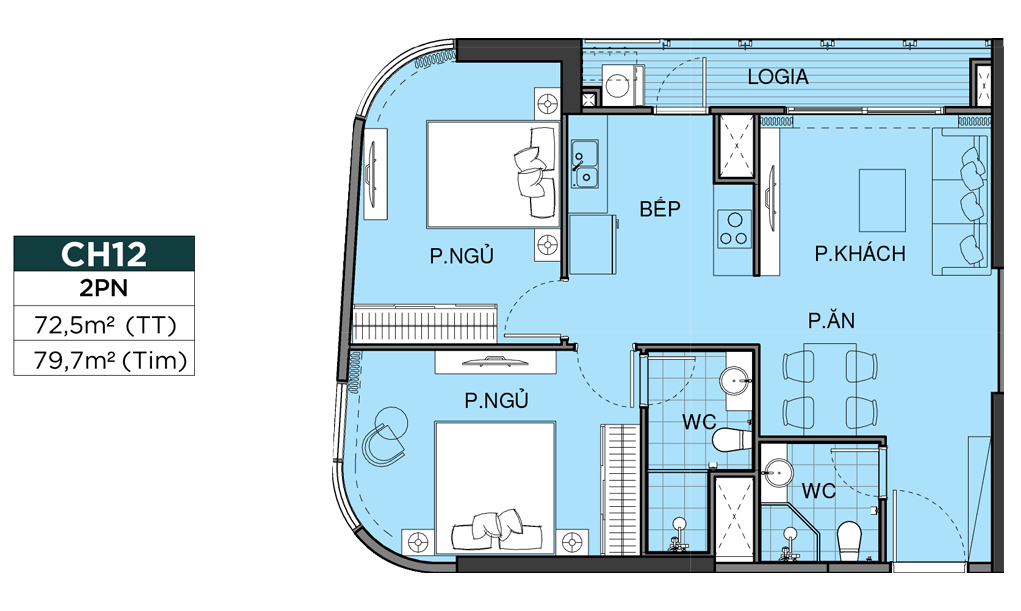
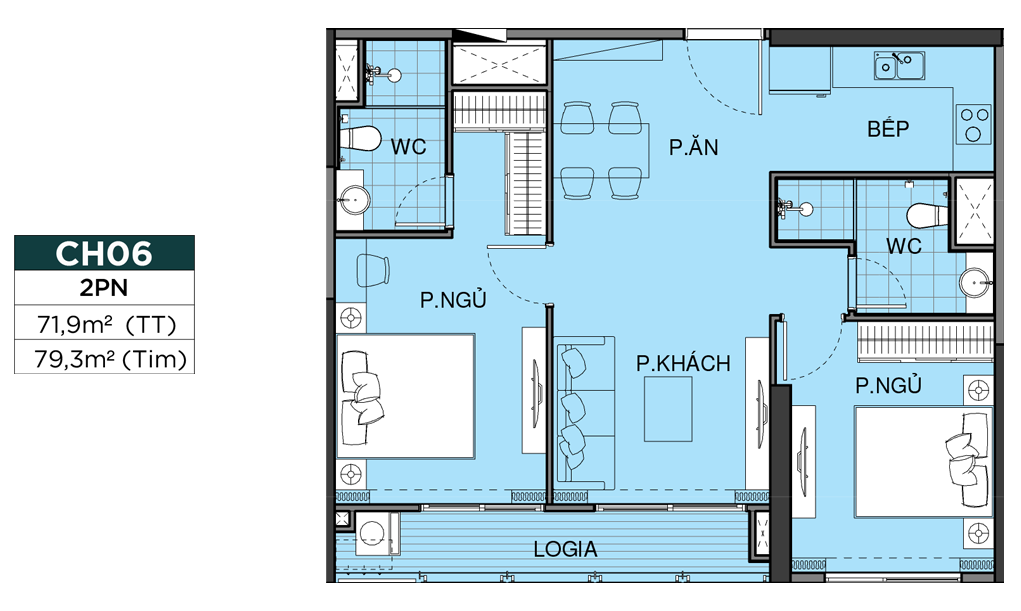
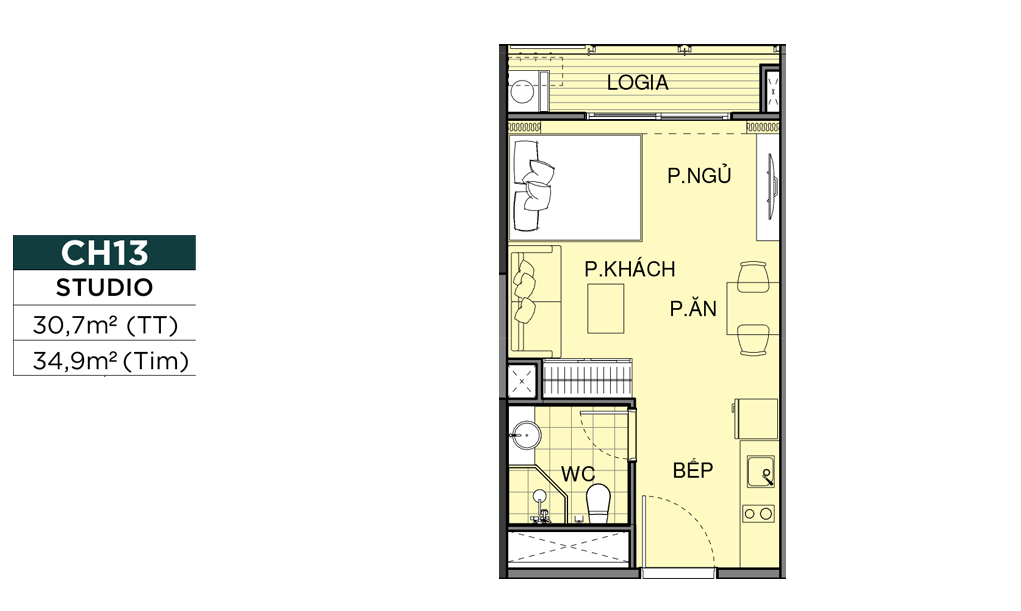
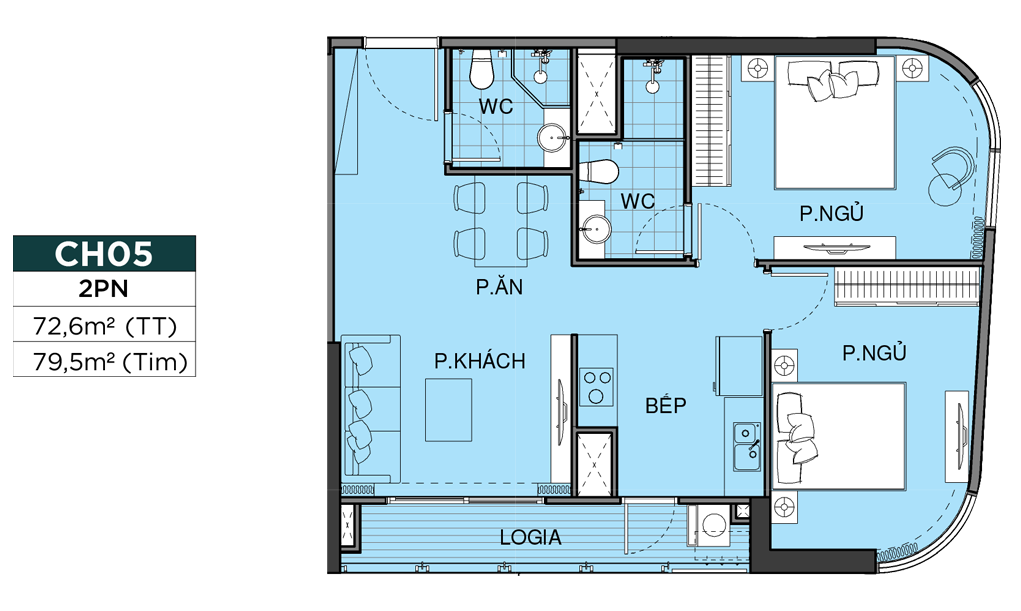
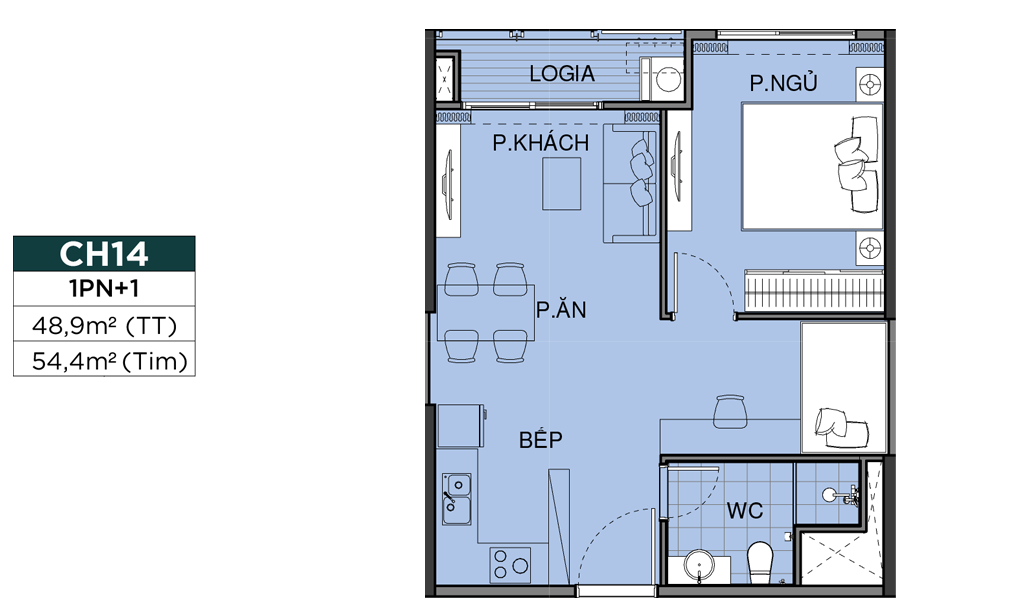
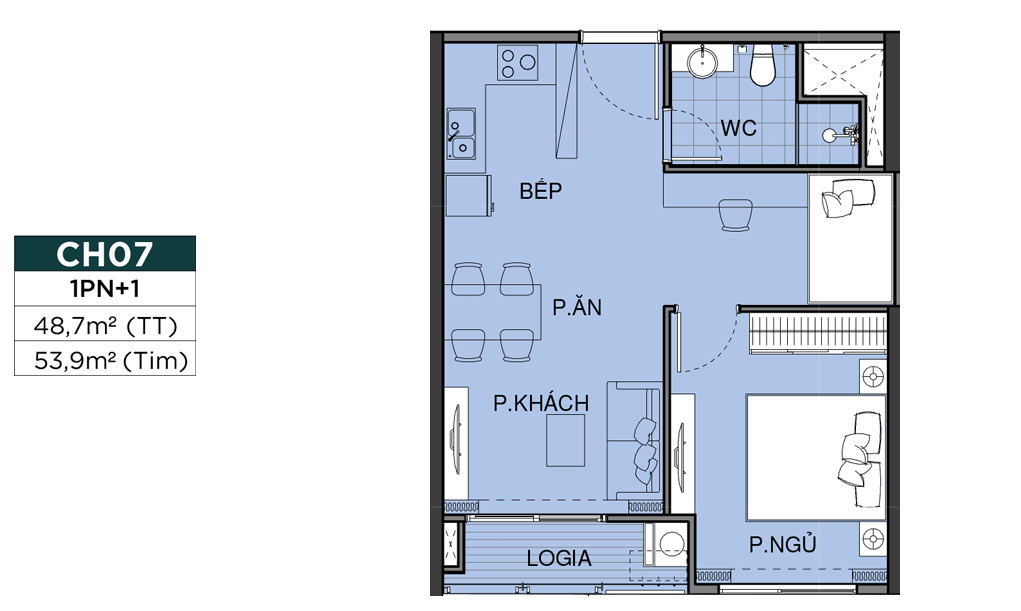
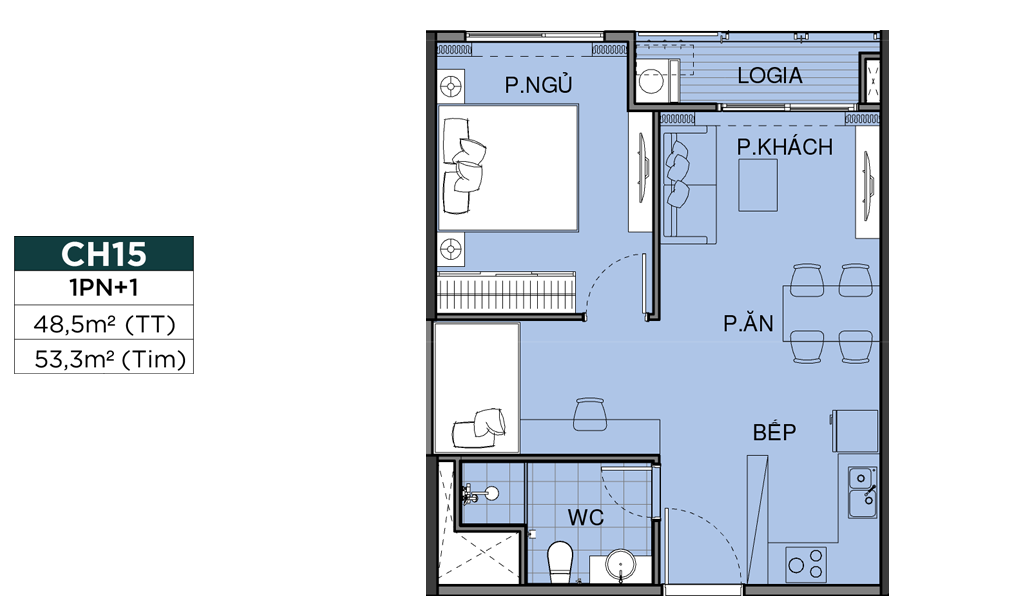
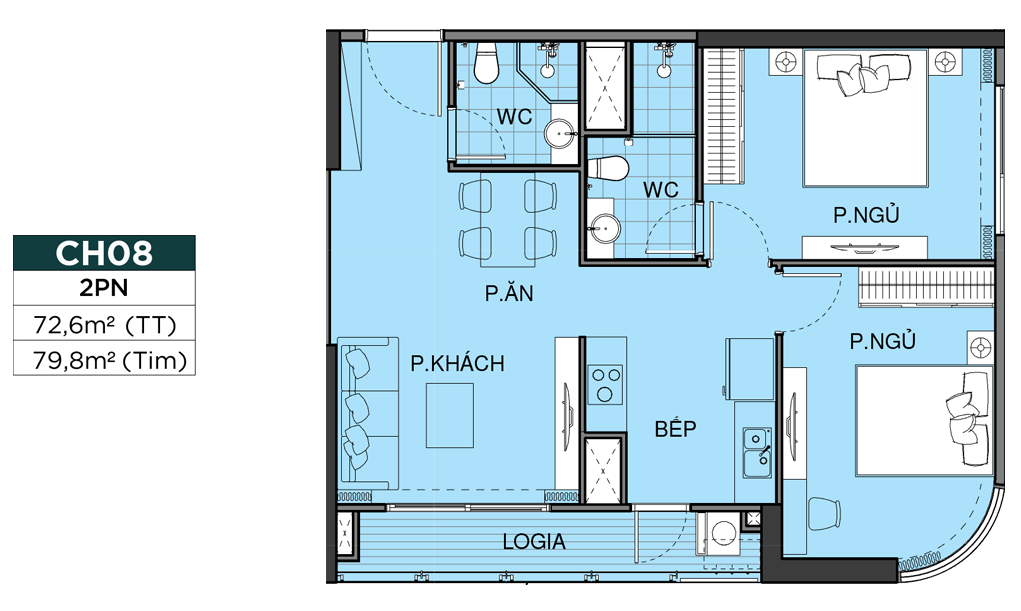
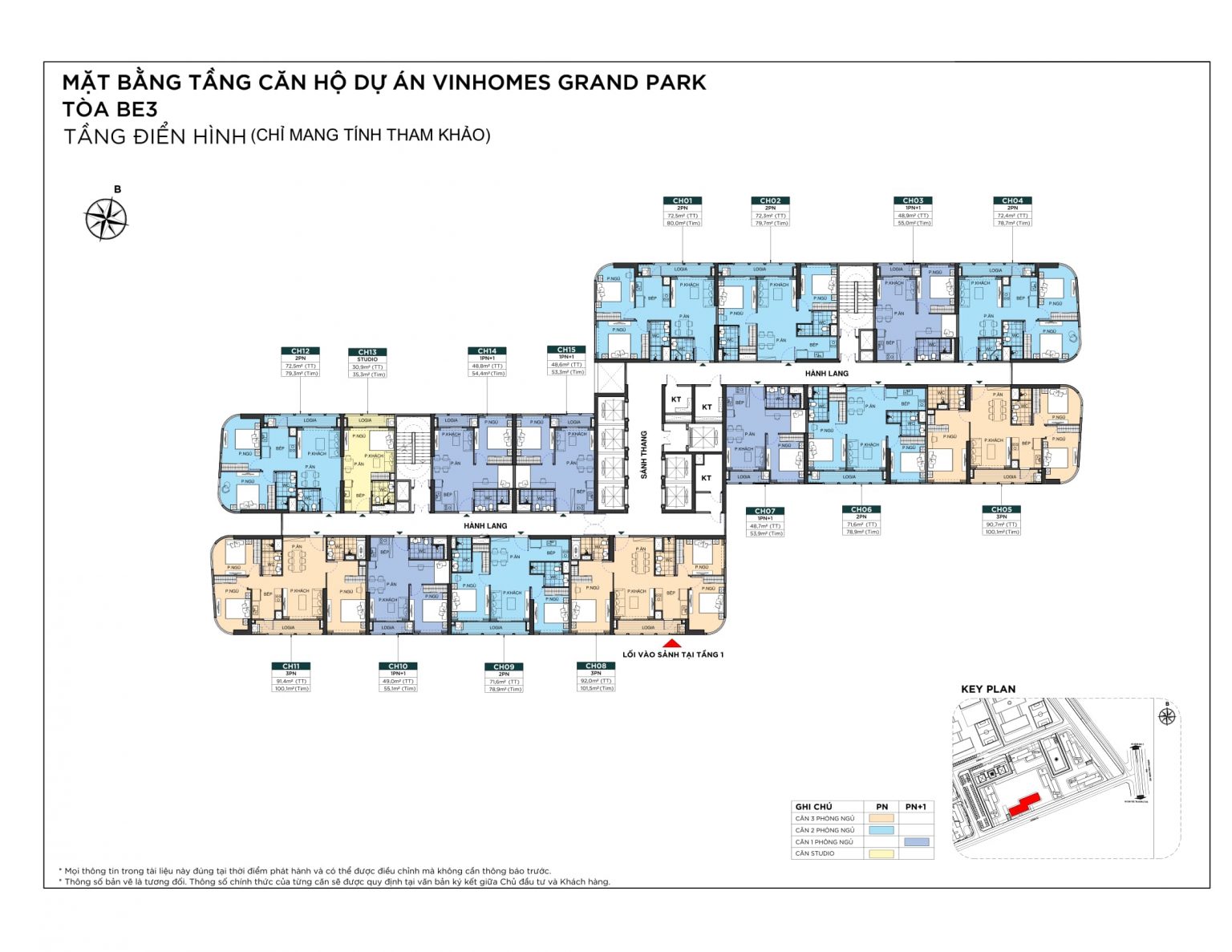
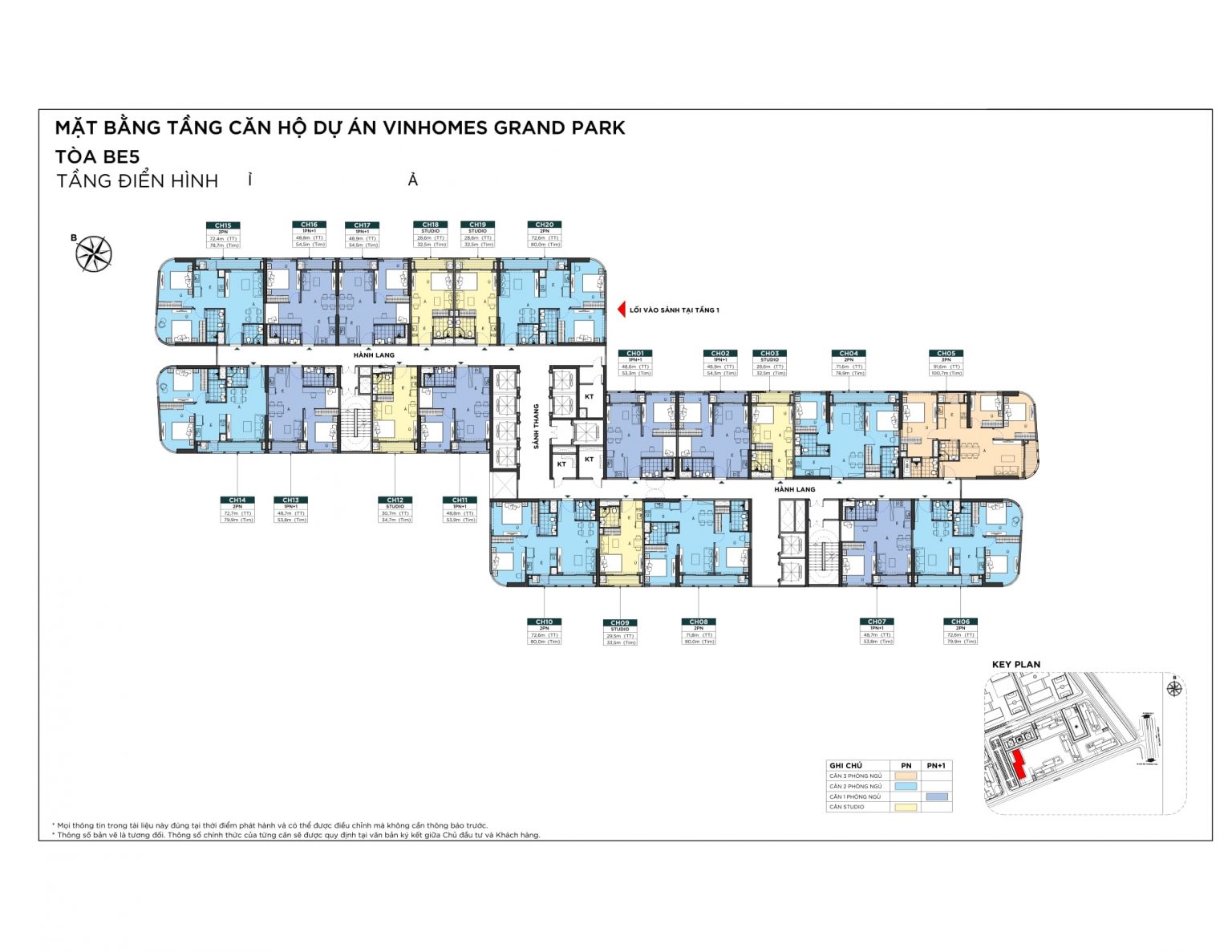
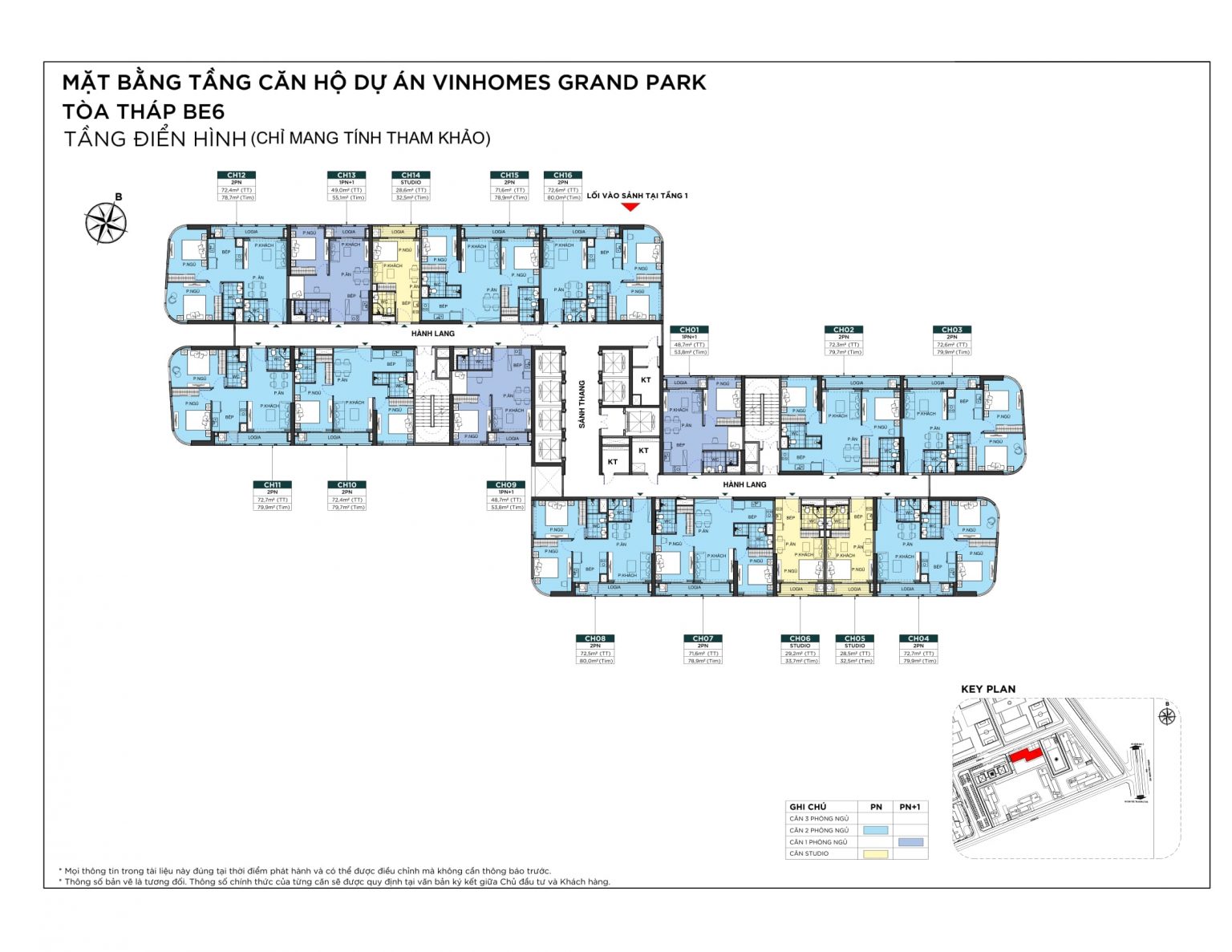
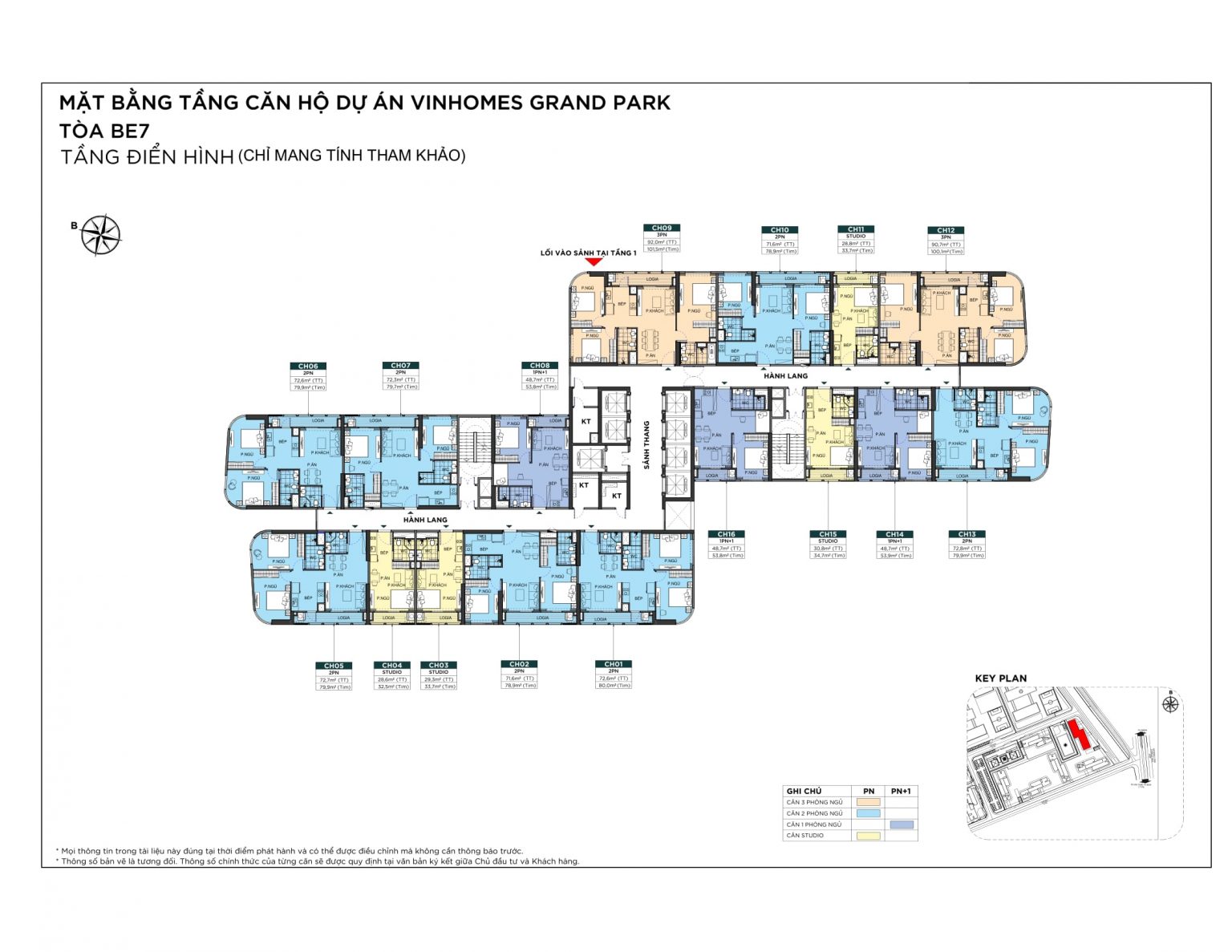
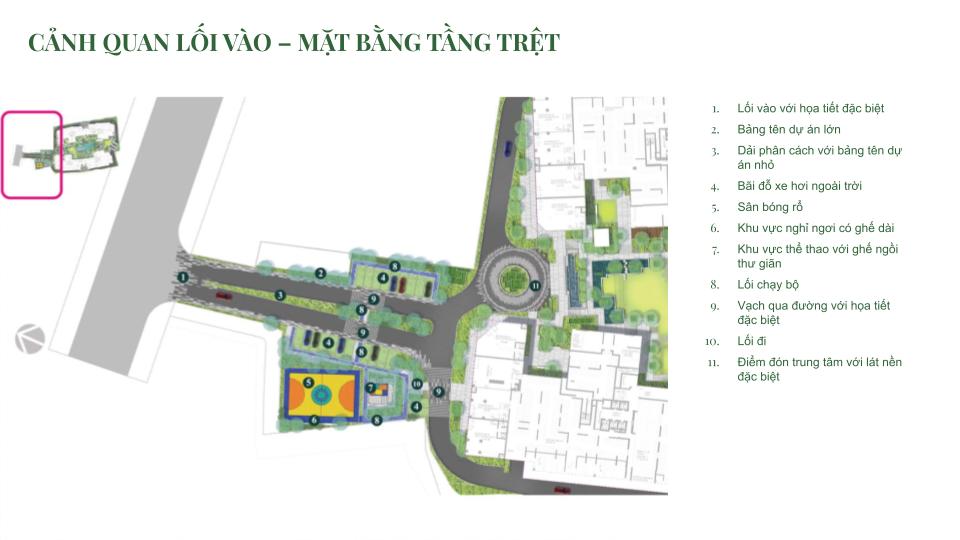
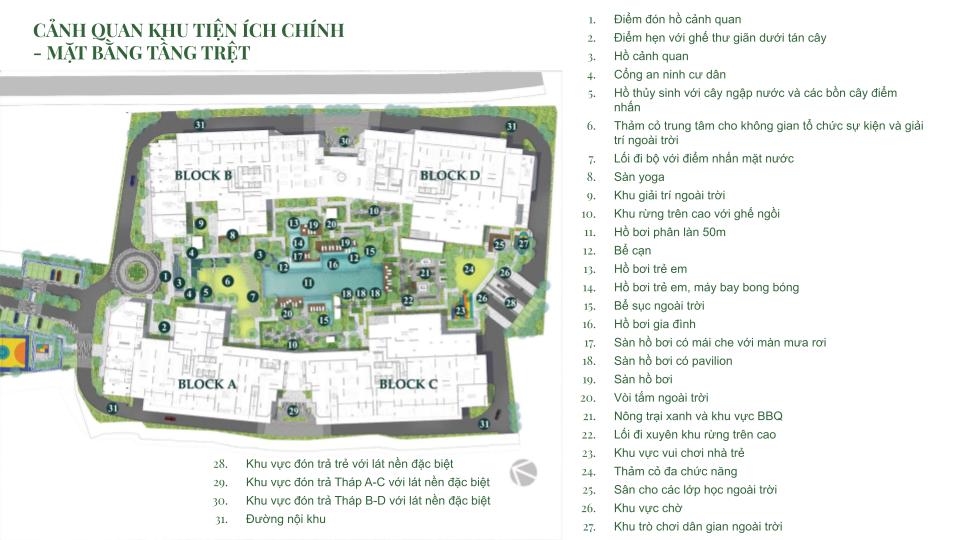
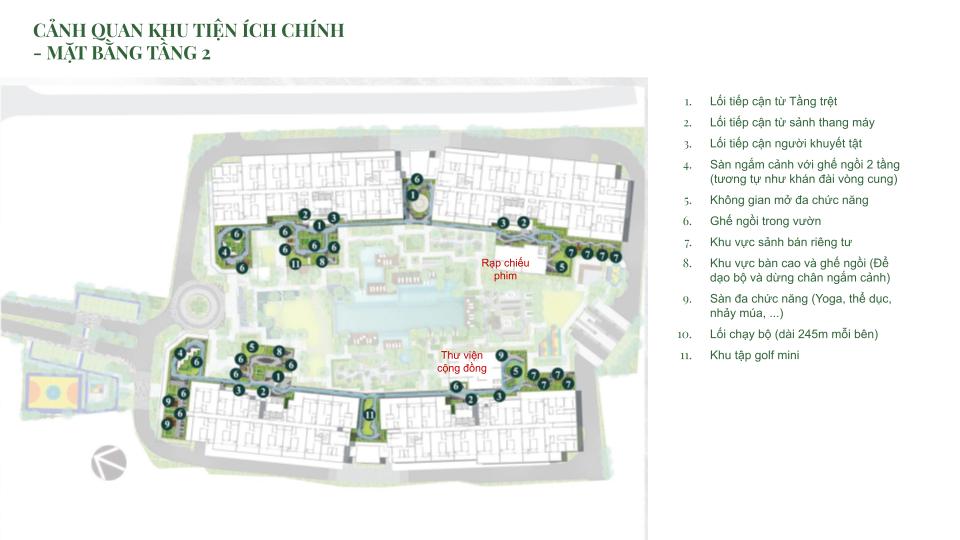
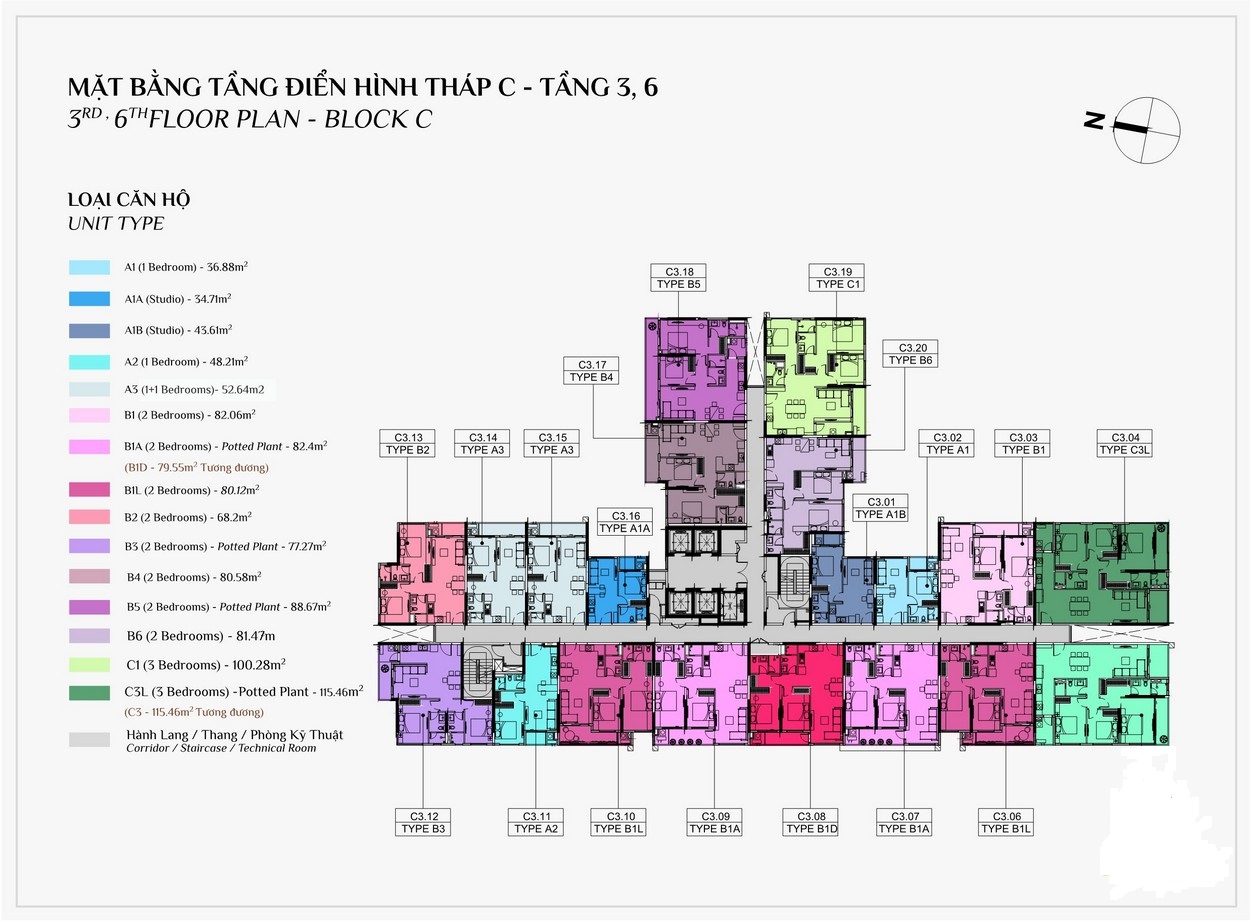
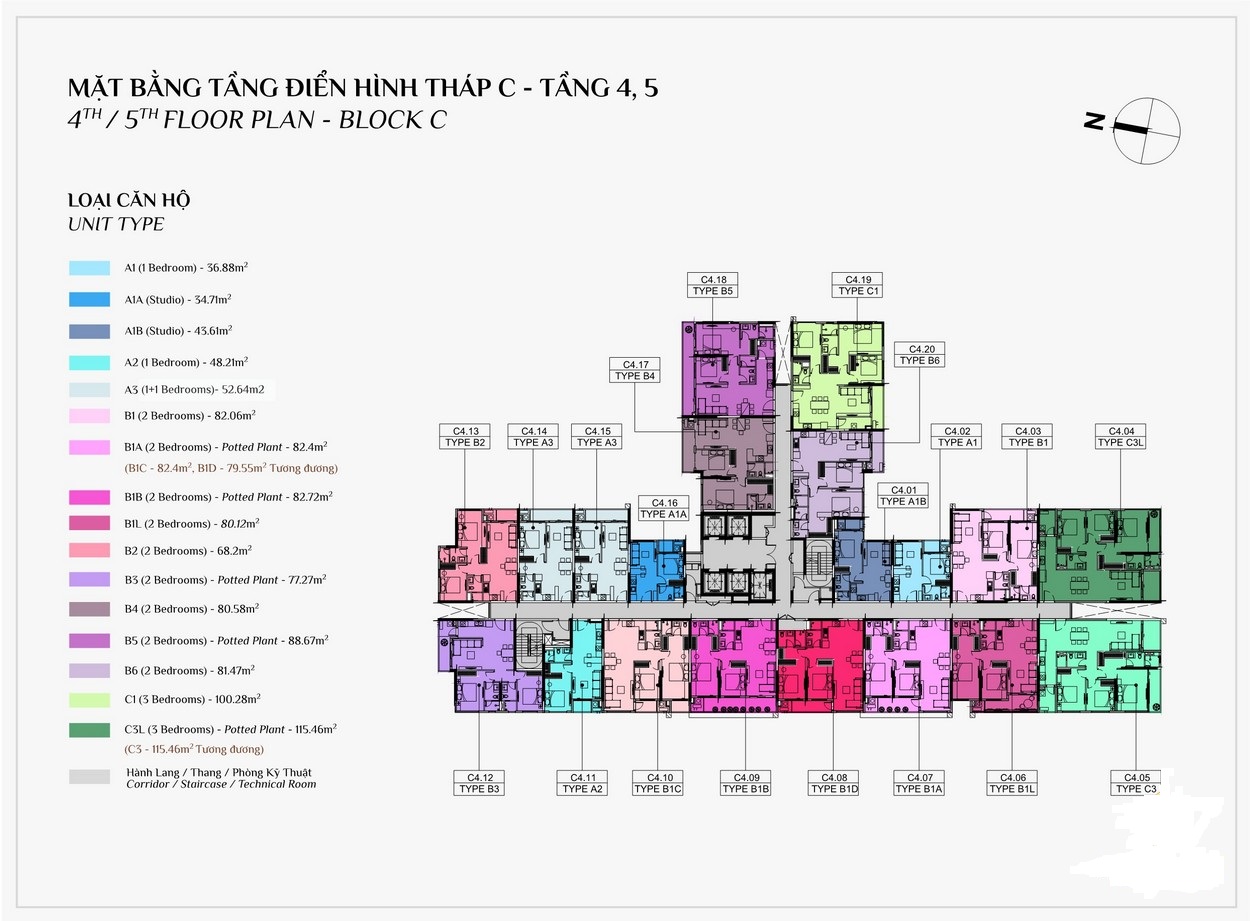
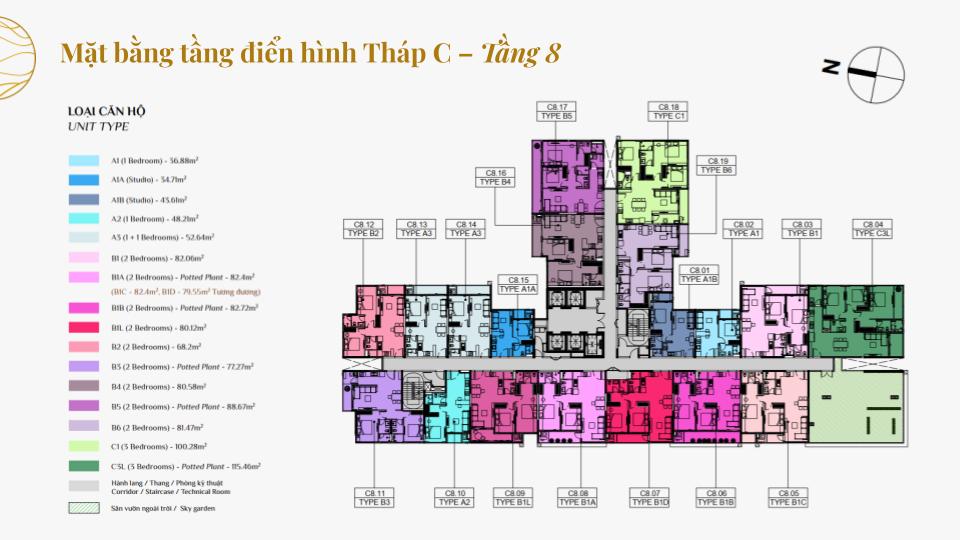
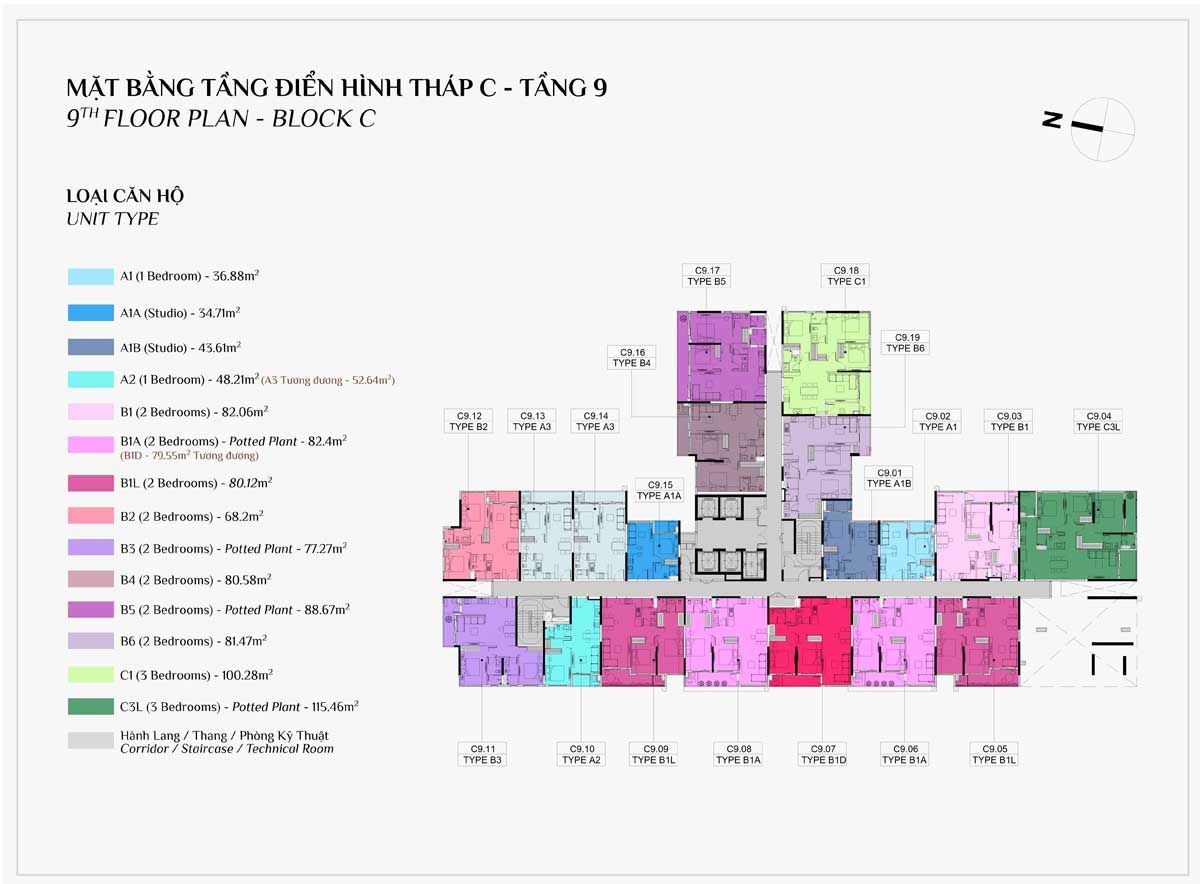
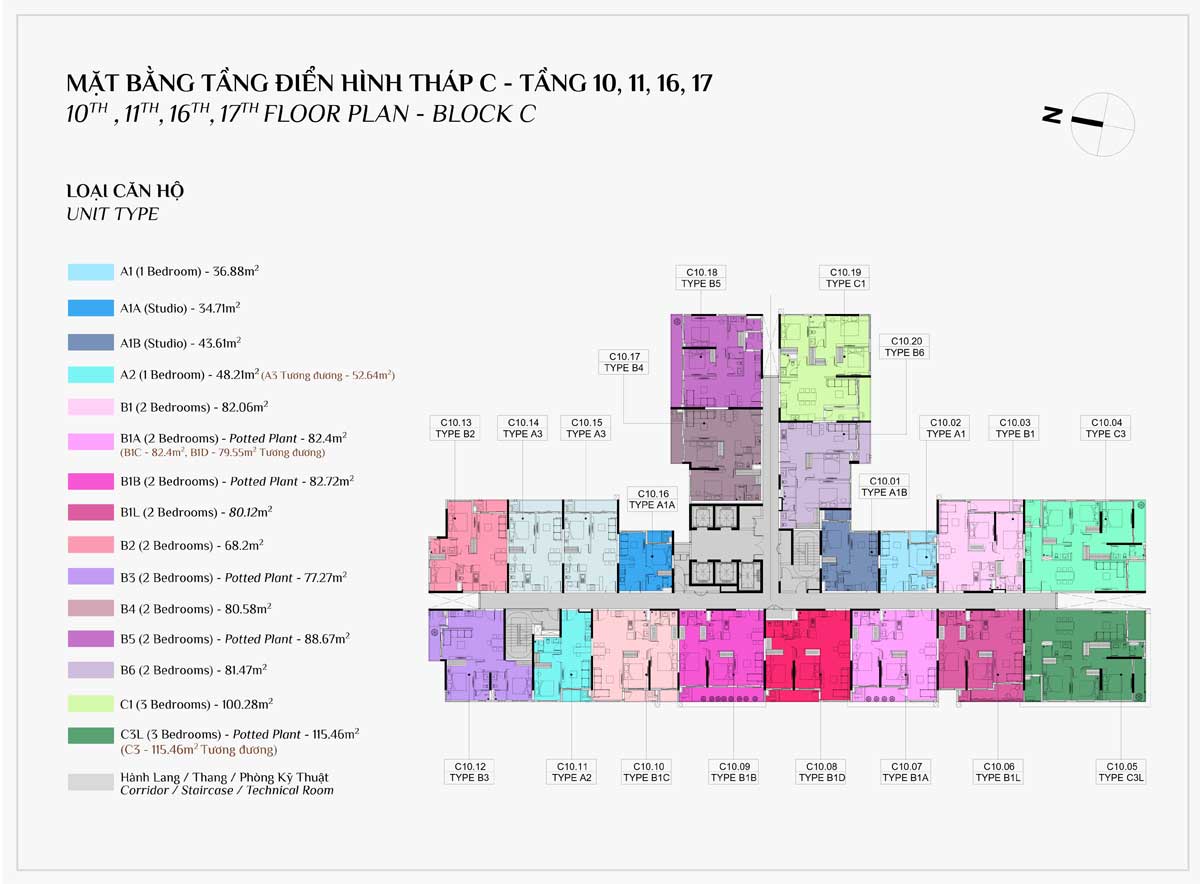
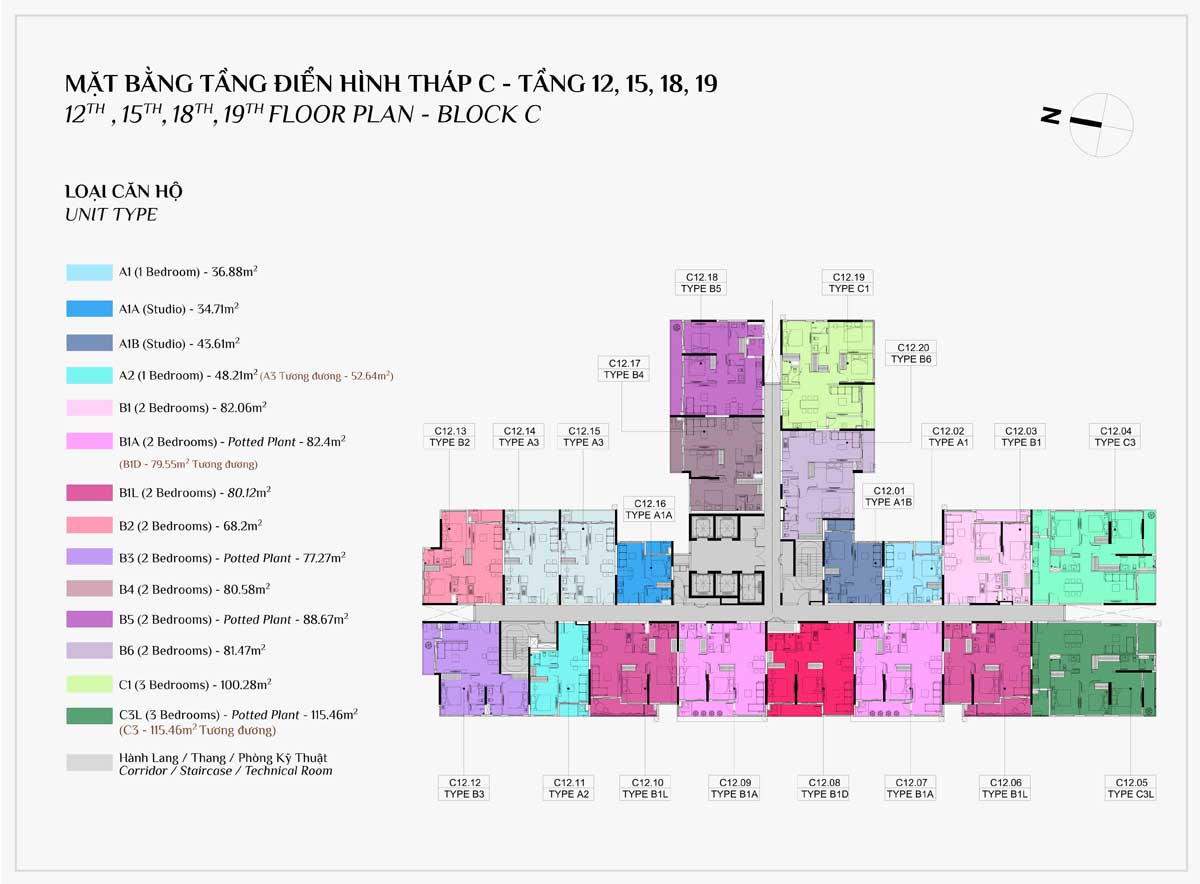
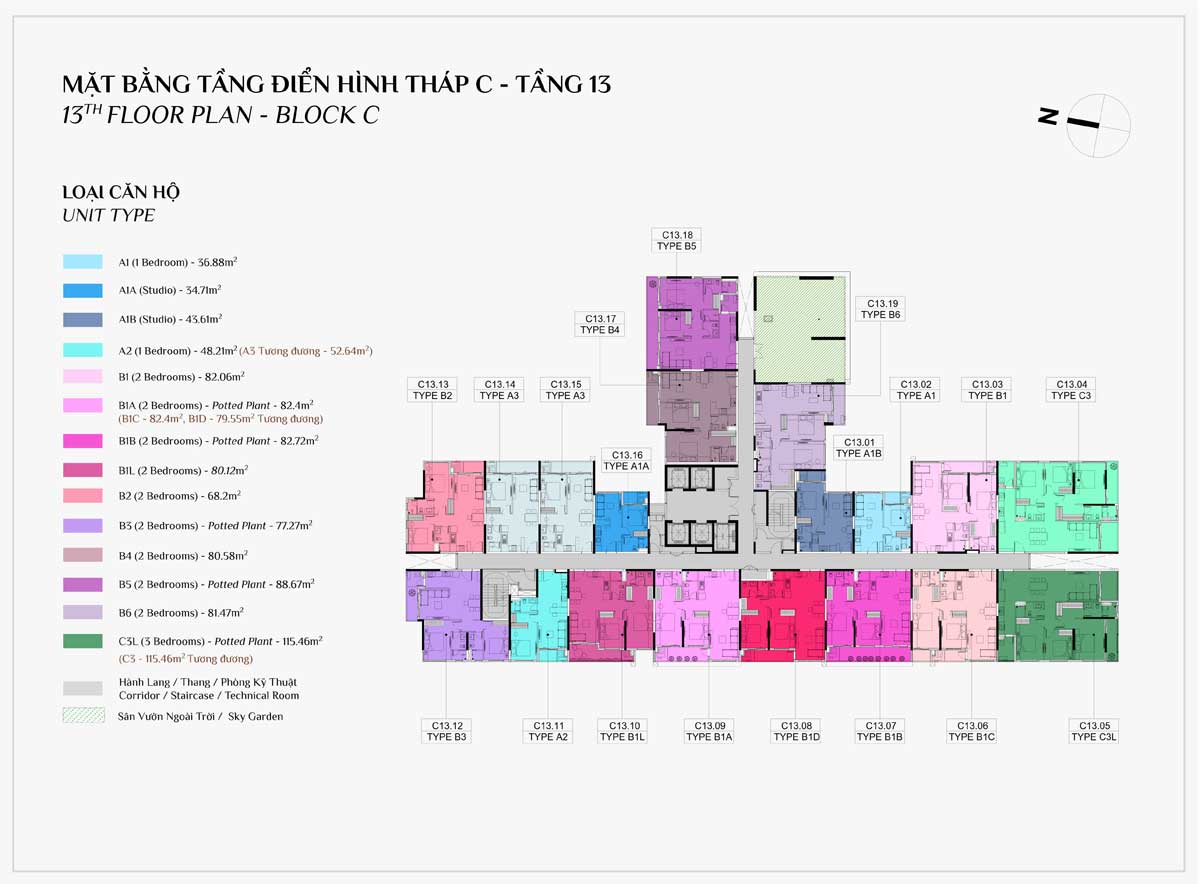
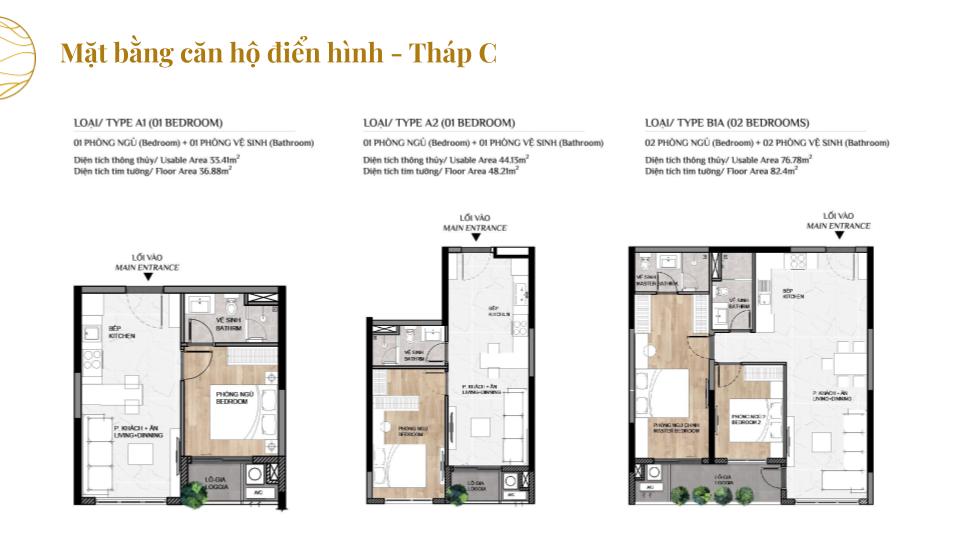
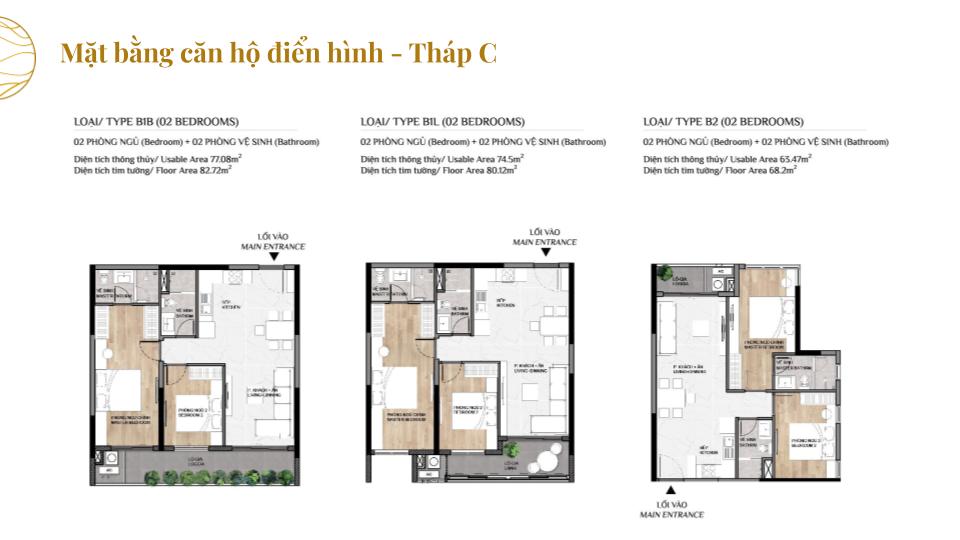
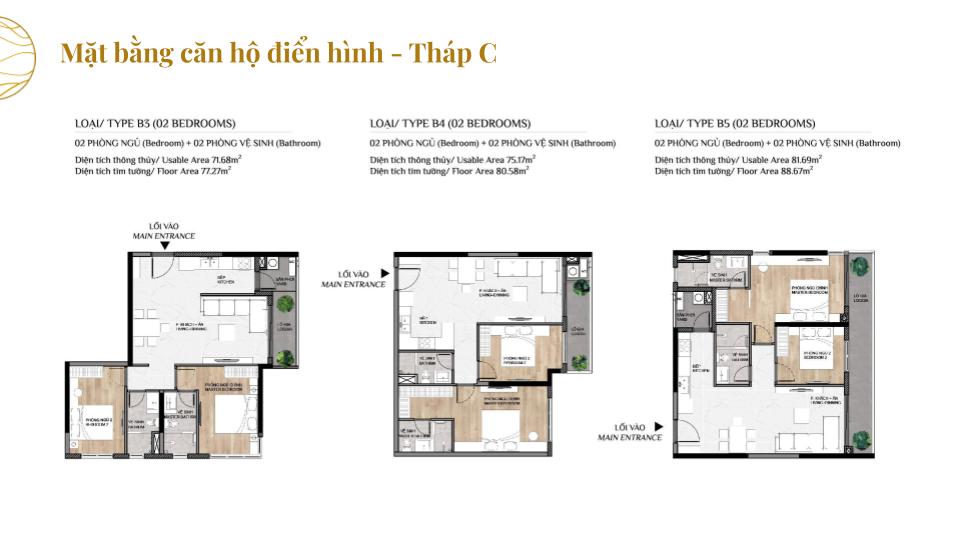
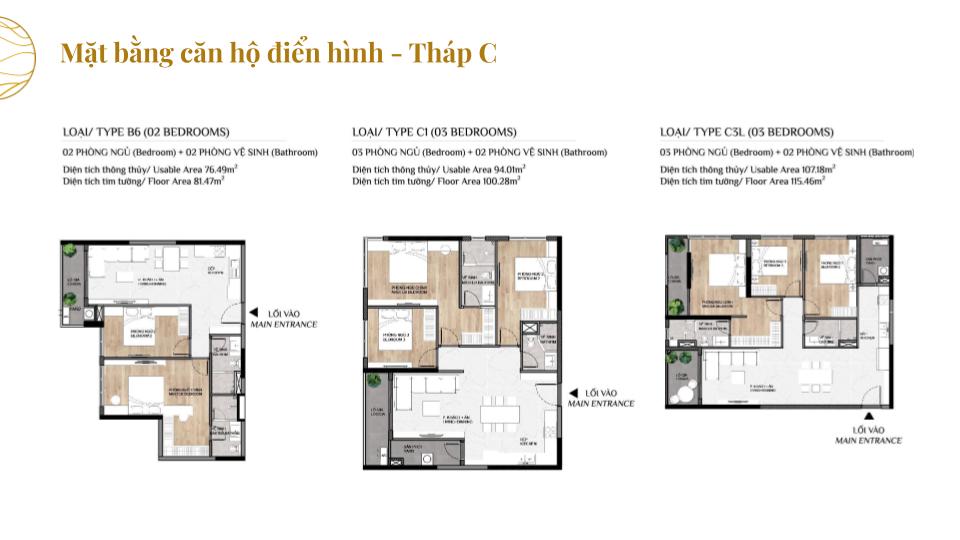
MẶT BẰNG CĂN HỘ
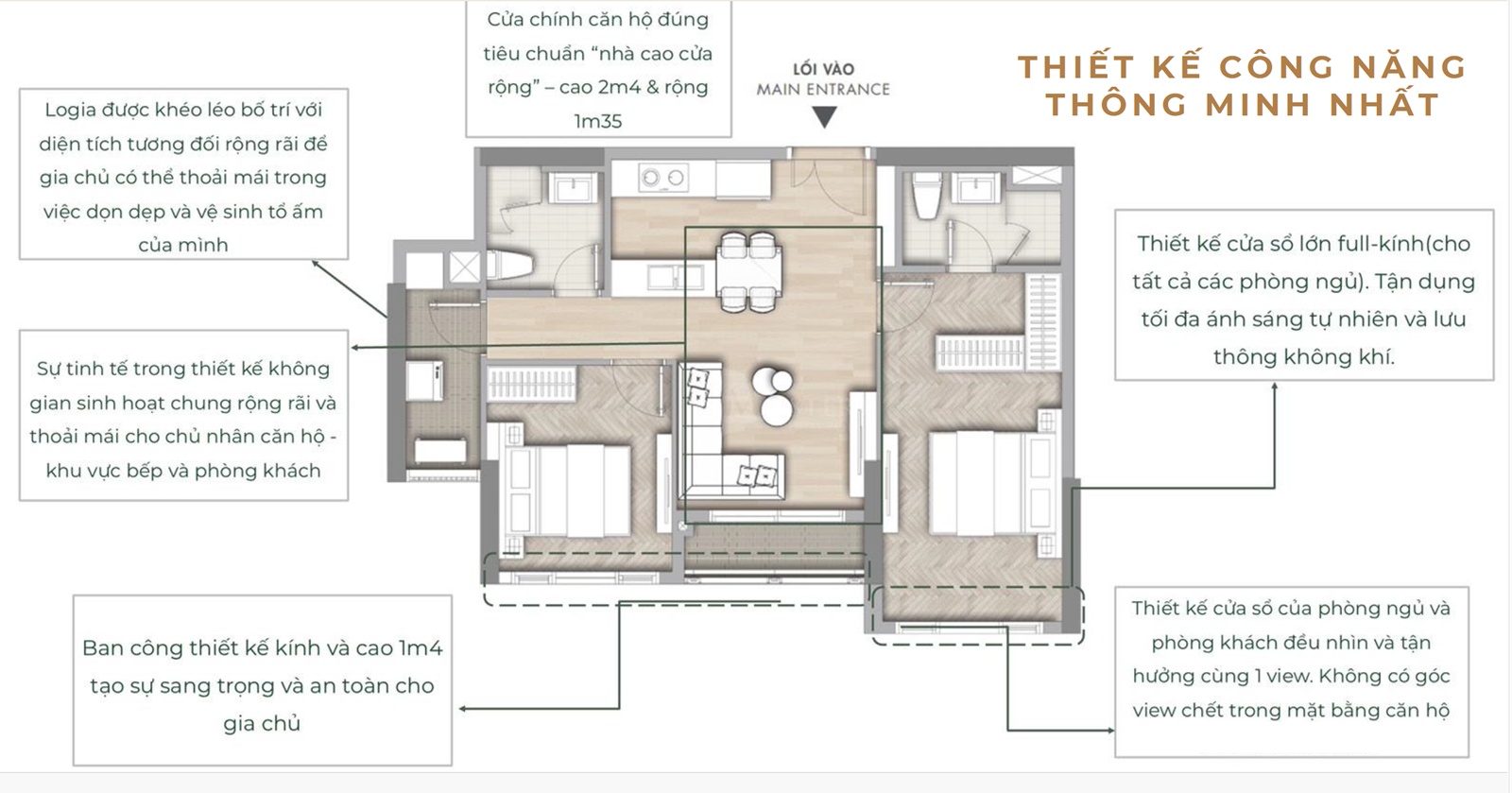
THIẾT KẾ CĂN HỘ
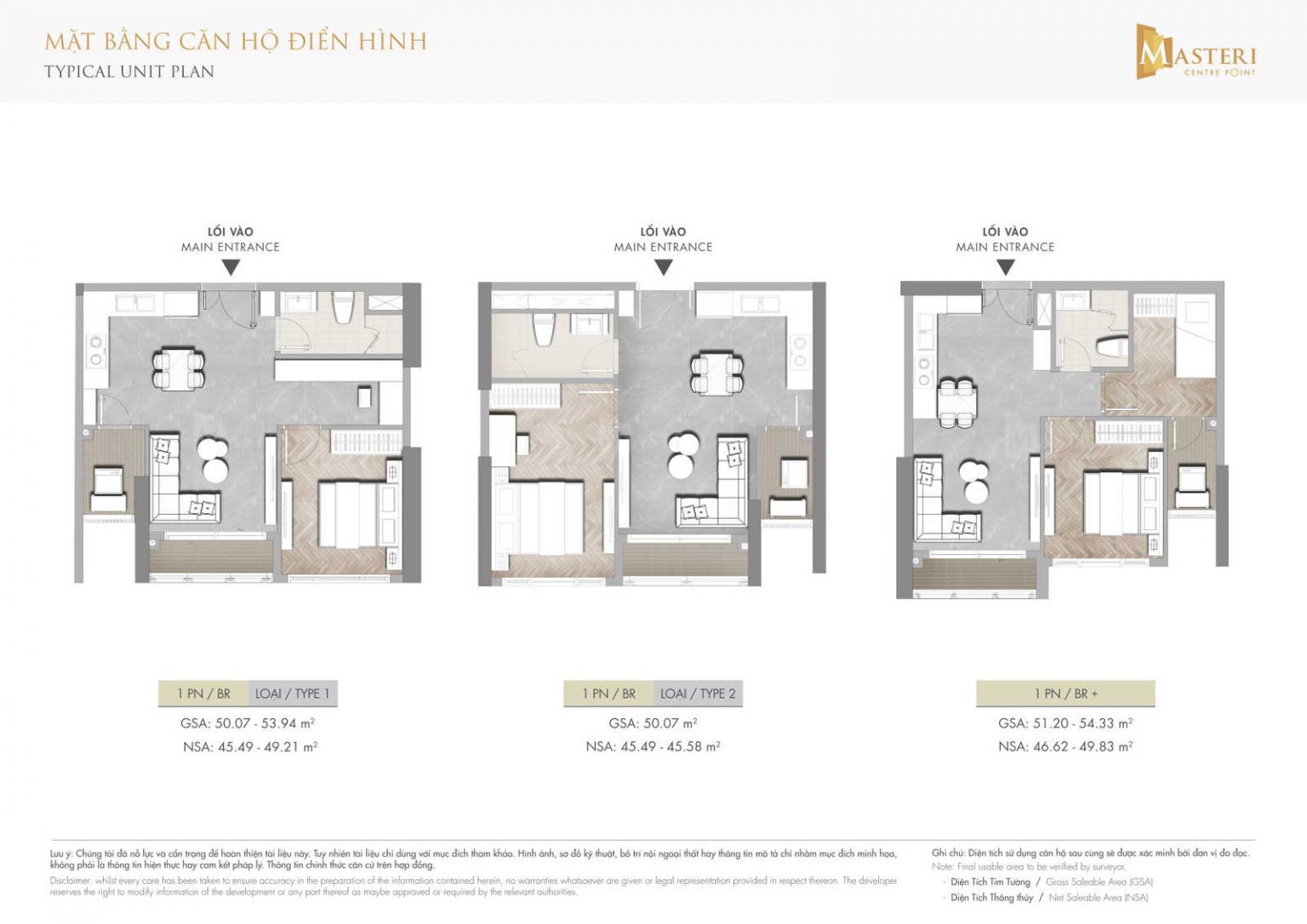
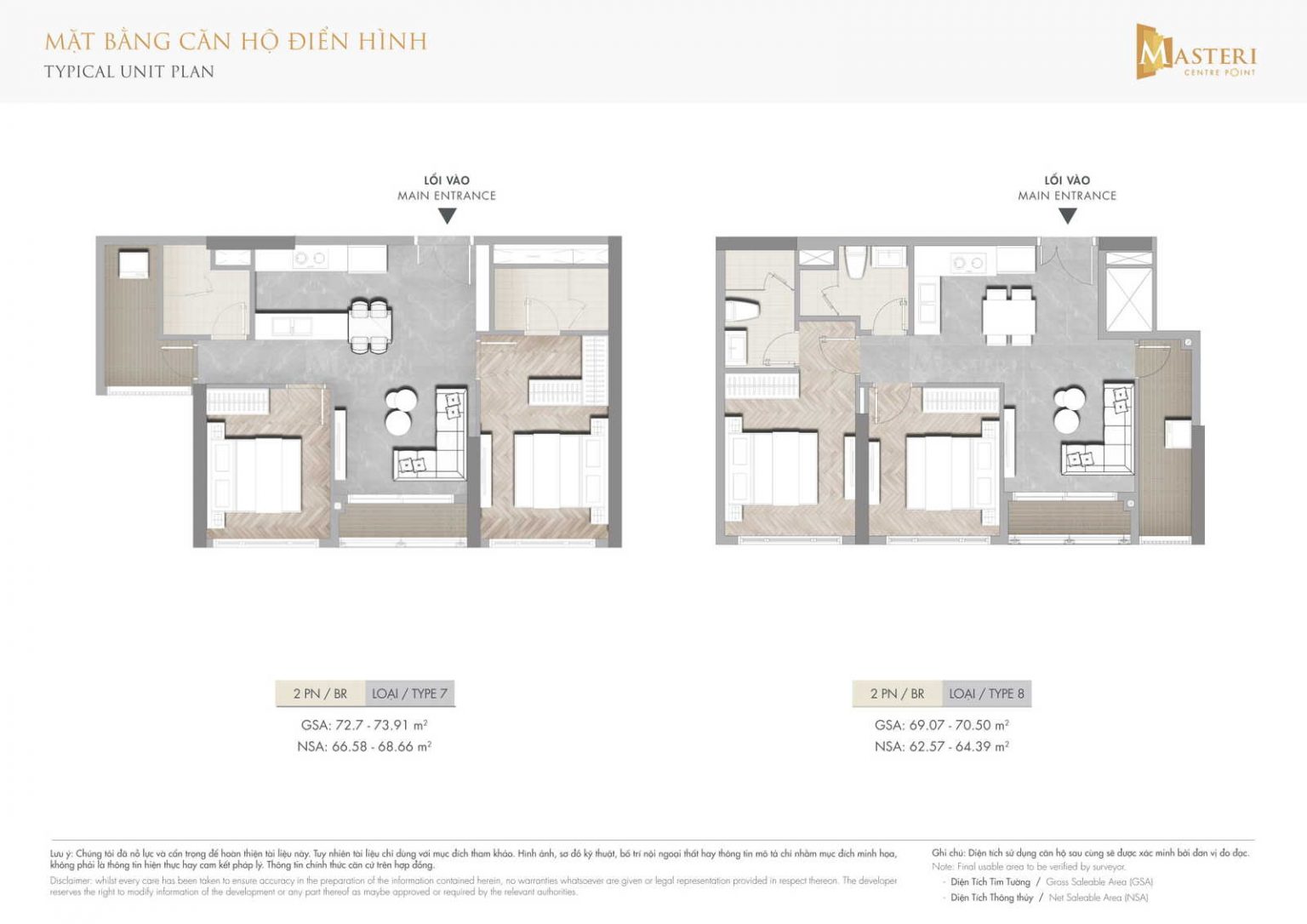

 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
CHÍNH SÁCH NHẬN NHÀ
 |
 |
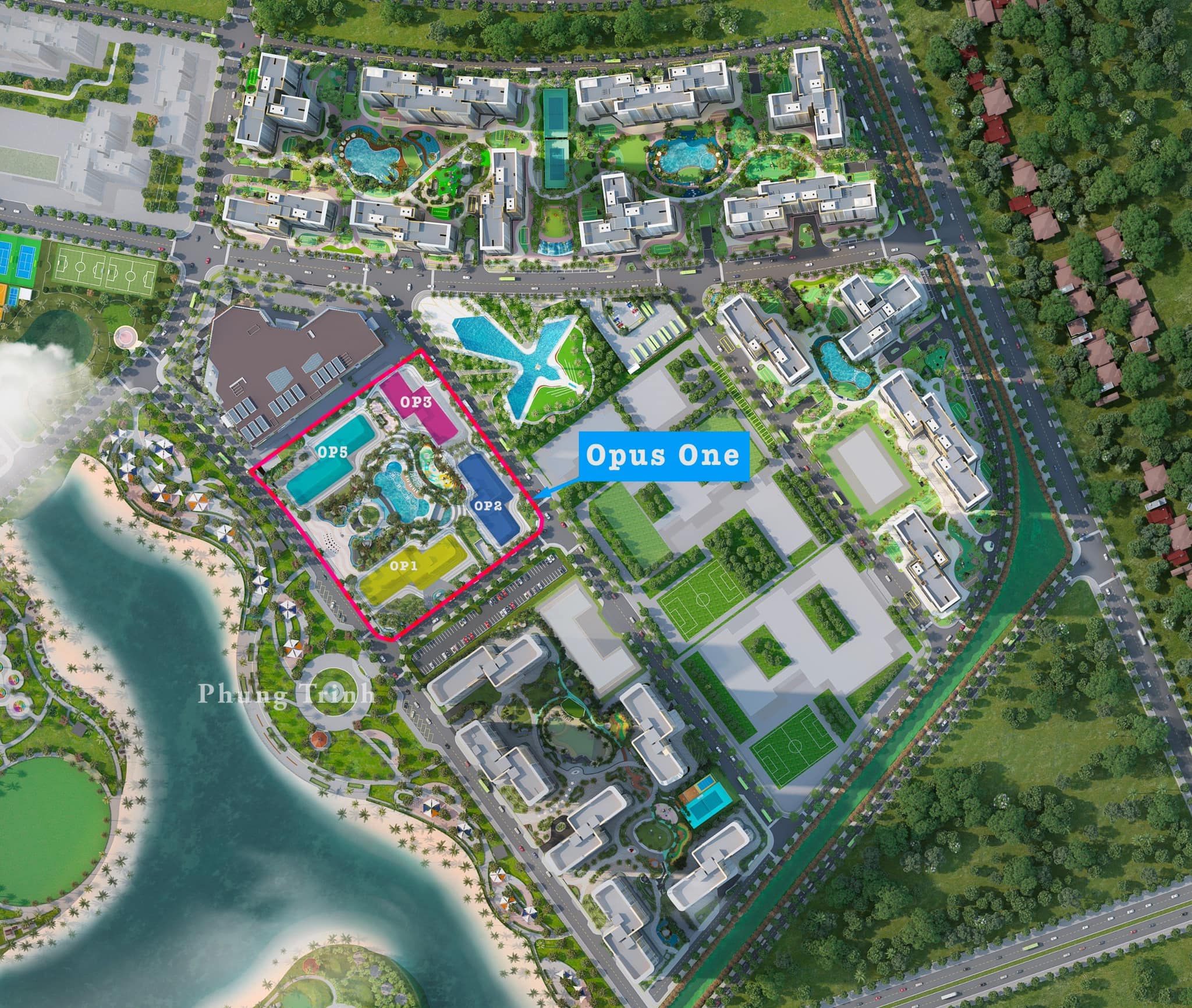
Phân khu The Opus One - Dự án Vinhomes Grand Park
The Opus One tiếp tục là phân khu cao tầng thứ 6 được chủ đầu tư Vinhomes cung ứng ra thị trường và Đây sẽ là phân khu căn hộ Compound cao cấp nhất tại Đại đô thị Vinhomes Grand Park với quy mô dự 4 toà tháp với 2.000 căn hộ.

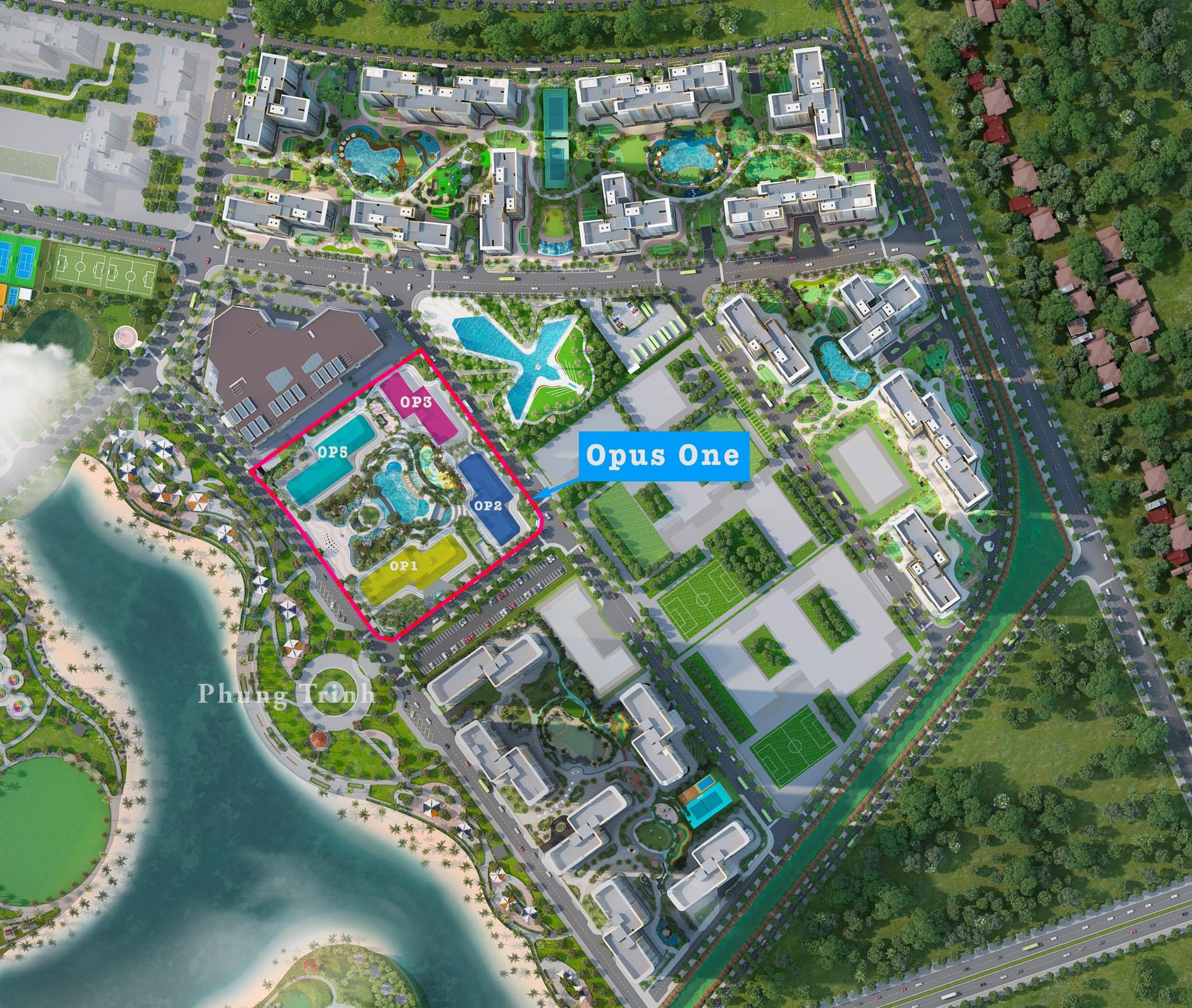
Phân khu căn hộ The Opus One mang ngôn ngữ thiết kế đẳng cấp vượt trội với phong cách resort tiêu chuẩn. Đặc biệt phân khu căn hộ này còn được thừa hưởng vị trí kim cương đắt giá mà đại đô thị Vinhomes Grand Park mang lại. Địa thế phong thủy có 1 – 0 – 2 đón đầu sự thịnh vượng và may mắn. Ngoài ra, Phân Khu The Opus One còn tọa lạc tại trung tâm đại đô thị Vinhomes Grand Park, nằm kế bên TTTM Vincom Mega Mall lớn nhất miền Nam, gần Ga Vinbus.

Phân khu ngoài sở hữu nhiều lợi thế từ đại đô thị lớn thì nơi đây cũng được đầu tư bài bản về mọi mặt. Hệ thống căn hộ 5 sao view đẹp. The Opus One được bao trọn bởi đại công viên rộng 36ha có quy mô lớn nhất Đông Nam Á mang đến không gian sống đẳng cấp, xanh mát đáng sống hiếm có khó tìm.









Tổng quan dự án The Opus One
|
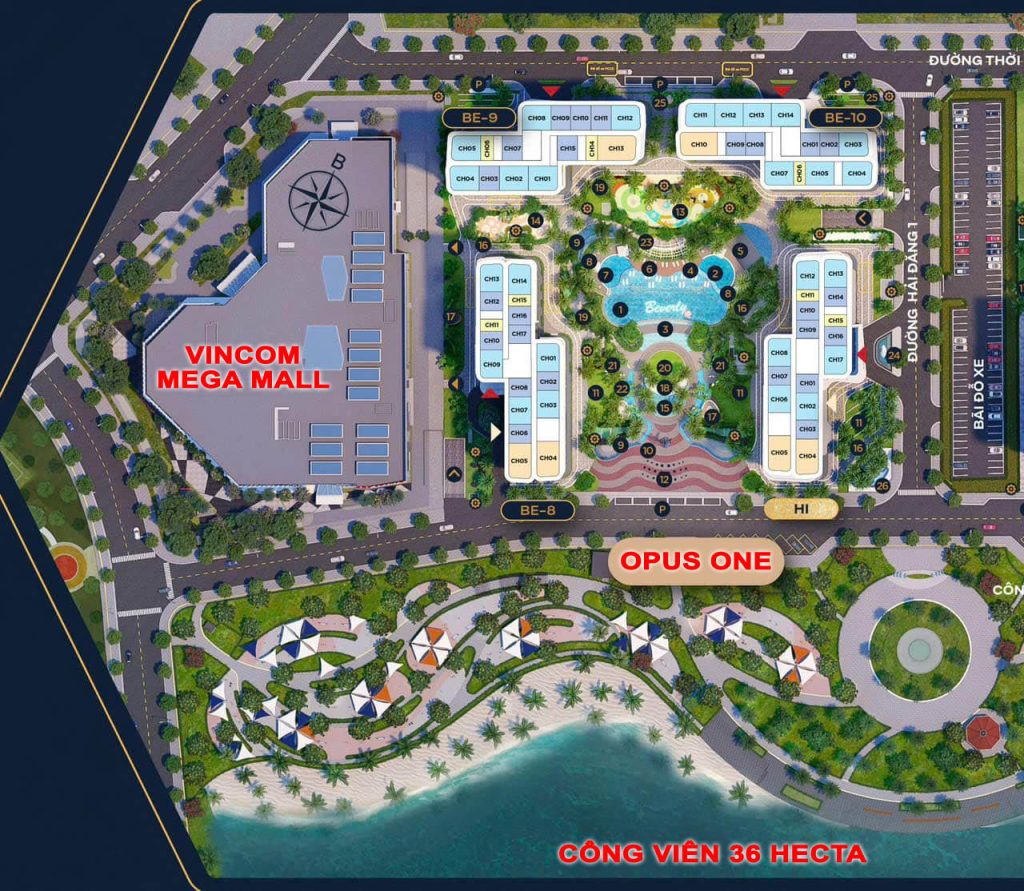 |
VỊ TRÍ PHÂN KHU THE OPUS ONE
TIỆN ÍCH CĂN HỘ THE OPUS ONE







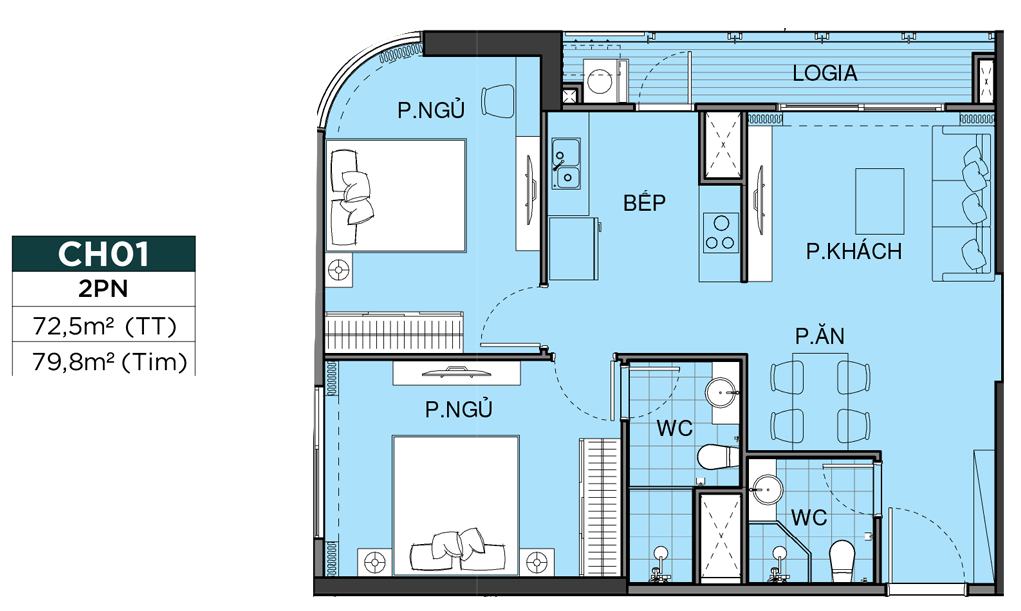
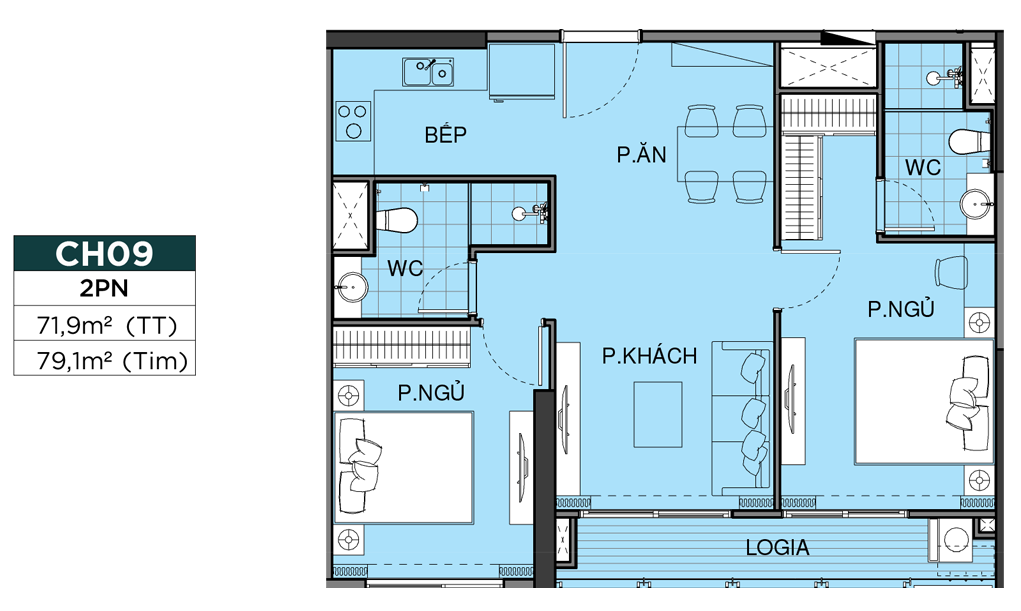
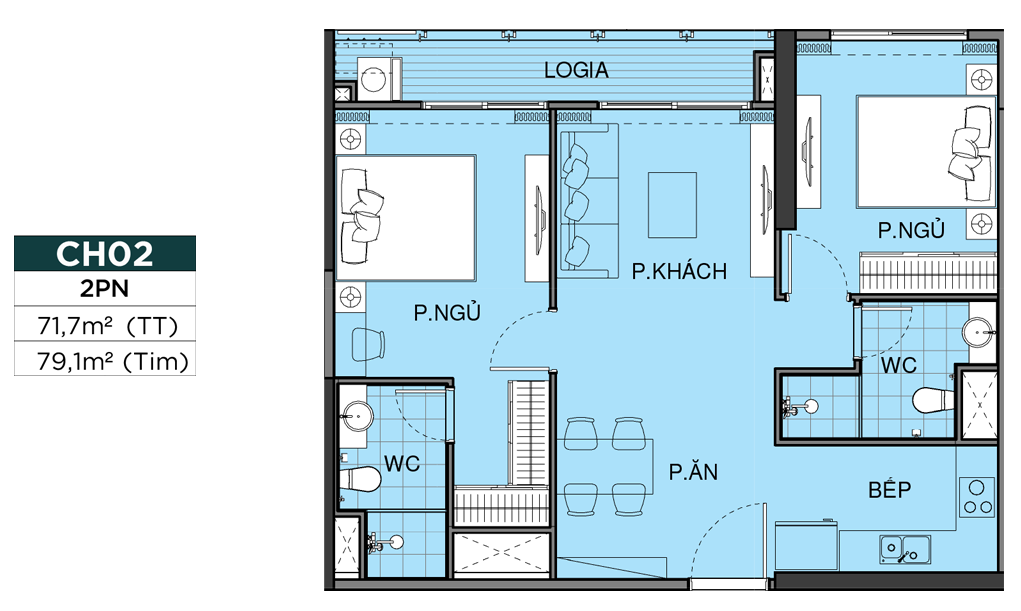
MẶT BẰNG CĂN HỘ THE OPUS ONE

 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
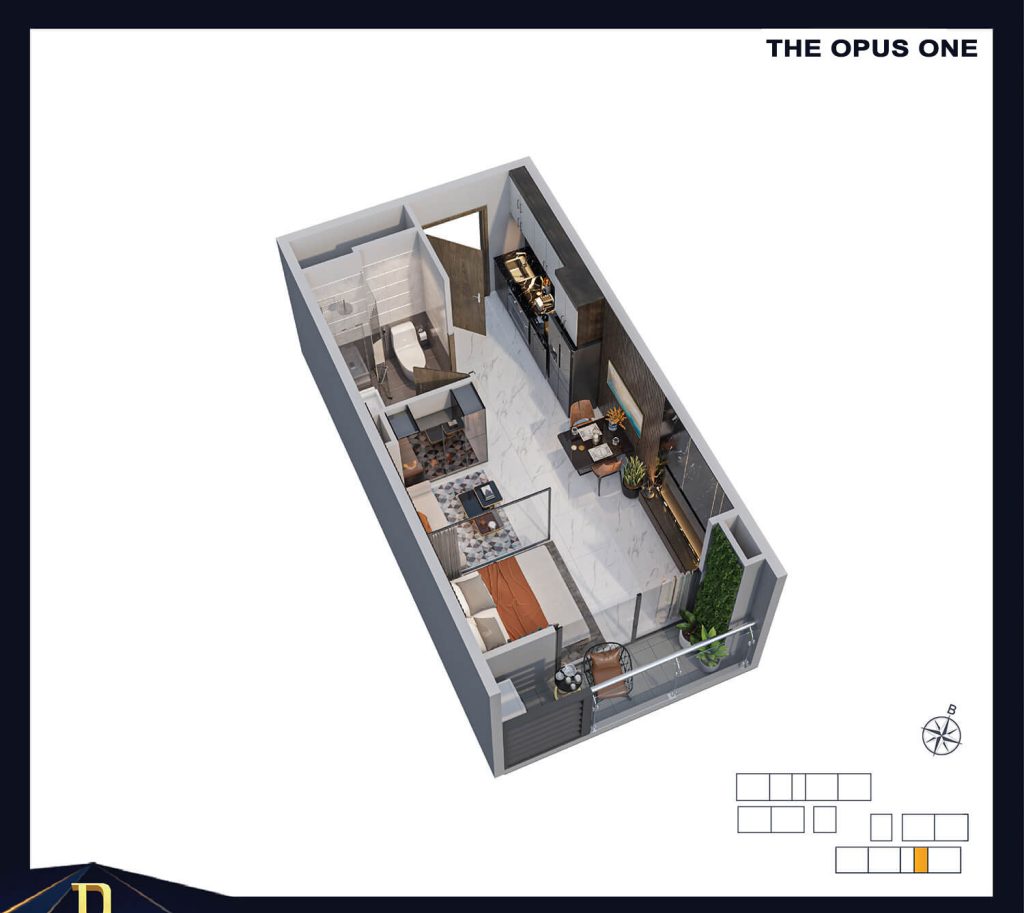 |
 |
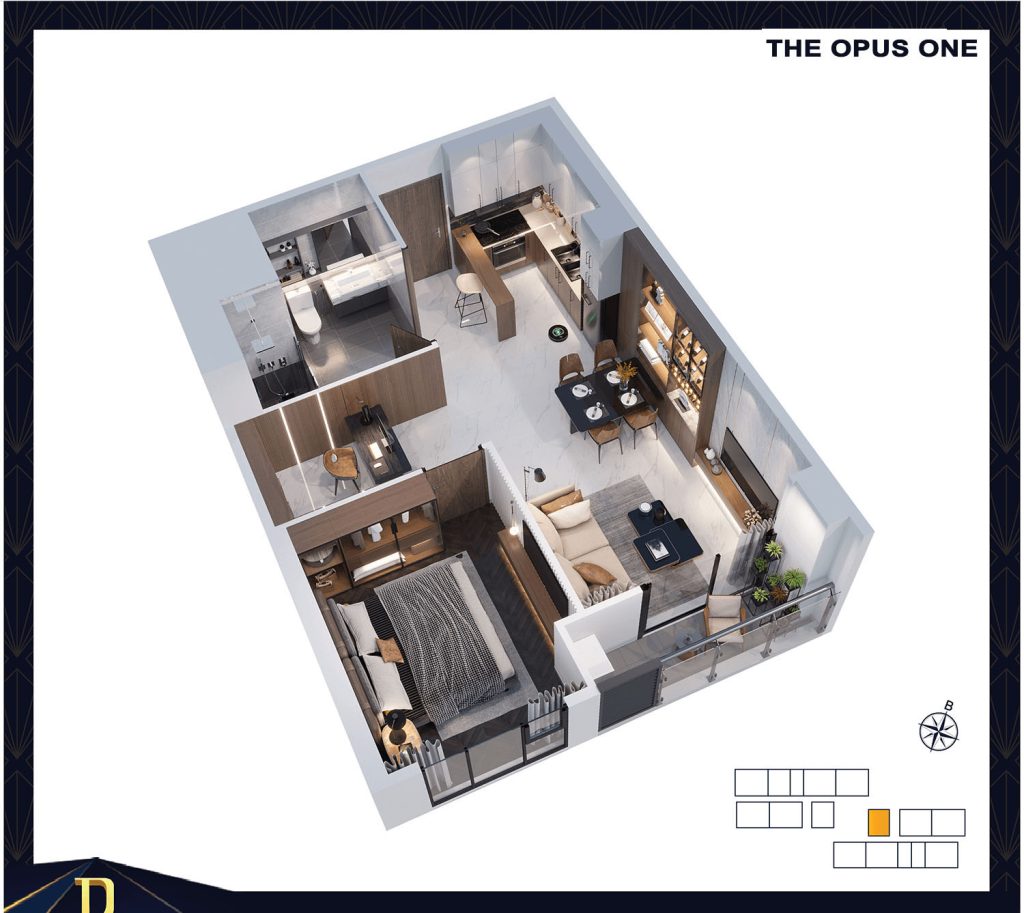 |
 |
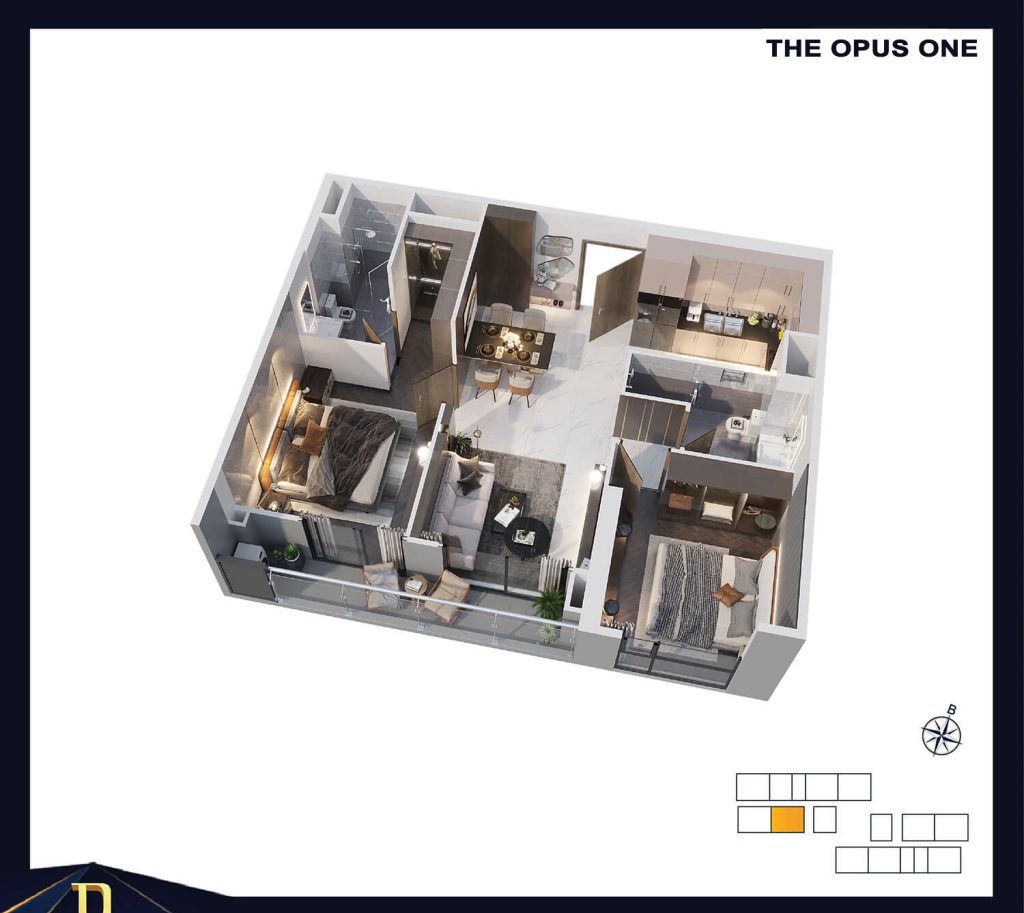 |
CĂN HỘ MẪU THE OPUS ONE



TIẾN ĐỘ DỰ ÁN




Phân khu The Manhattan - Dự án Vinhomes Grand Park
The Manhattan là phân khu thấp tầng của dự án Vinhomes Grand Park được tọa lạc tại góc đường Vành Đai 3 – Phước Thiện, Long Bình, thành phố Thủ Đức, thành phố Hồ Chí Minh do Tập đoàn danh tiếng Vingroup làm chủ đầu tư. Ngay khi ra mắt phân khu nhận được sự quan tâm nồng nhiệt của các nhà đầu tư. The Manhattan nắm giữ vị trí tuyệt đẹp khi ôm trọn công viên xanh 36ha Grand Forest xanh mát kết hợp với phong cách thiết kế sang chảnh của những dãy nhà phố, biệt thự đẳng cấp quốc tế. Mở ra lối sống thịnh vượng, mang đến cho cư dân những trải nghiệm thú vị giữa lòng thành phố xa hoa.

Tổng quan dự án The Manhattan
| Tên phân khu | The Manhattan – Vinhome Grand Park |
| Chủ đầu tư | VinGroup |
| Vị trí | Góc đường Vành đai 3 – Phước Thiện, dự án Vinhomes Grand Park, Long Bình, thành phố Thủ Đức, thành phố Hồ Chí Minh |
| Đơn vị thiết kế | Artelia Group |
| Quy mô | 550 căn |
| Loại hình sản phẩm | Nhà phố (shophouse), biệt thự đơn lập, biệt thự song lập, shop villa |
| Ngân hàng hỗ trợ | Techcombank cho vay 70%Ân hạn gốc và lãi suất 0% trong 18 tháng |
| Tiện ích nội khu | Trung tâm thương mại, công viên, nhà hàng, khách sạn, hồ bơi tràn bờ, khu vui chơi trẻ em, sân chơi thể thao… |
| Khởi công | Quý 2/ 2020 |
| Thời gian bàn giao | Quý 1/ 2021(dự kiến) |
| Pháp lý |
|
| Hình thức sở hữu |
|
| Giá bán dự kiến | 130 – 150 triệu/m2 |


The Manhattan tọa lạc tại Góc đường Vành đai 3 – Phước Thiện, dự án Vinhomes Grand Park, Long Bình, thành phố Thủ Đức, thành phố Hồ Chí Minh.
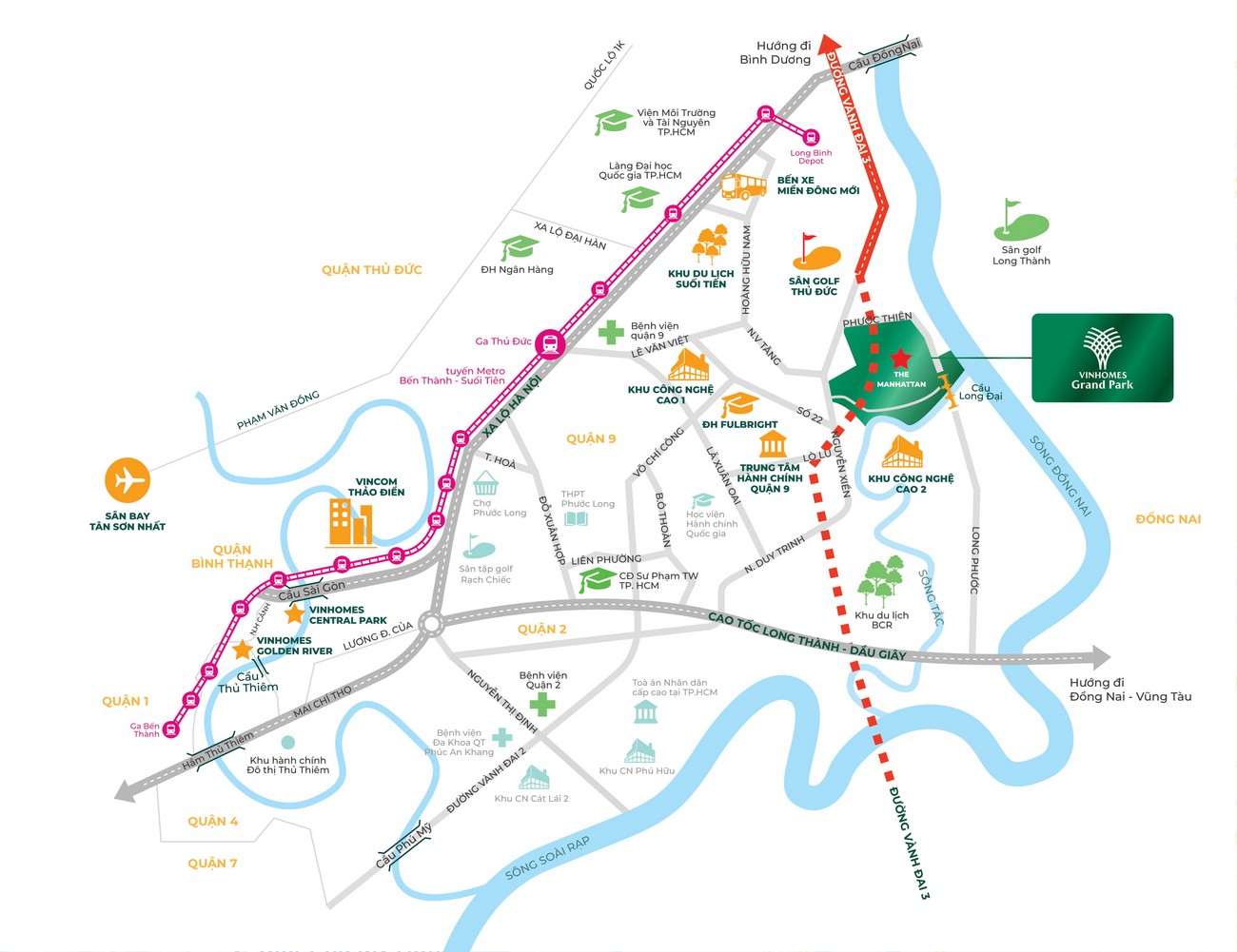
Sở hữu địa thế phong thủy cực thịnh với đầy đủ 3 tiêu chí “nhất cận thị, nhị cận giang, tam cận lộ mang đến những lợi thế vô cùng thuận lợi cho phân khu cụ thể như:Khả năng kết nối linh hoạt và thuận tiện từ phân khu tới các tỉnh miền Đông, miền Trung và miền Tây thông qua trục đường giao thông Xa Lộ Hà Nội, Quốc lộ 1, cao tốc quốc lộ 51…Cùng với khả năng kết nối nhanh chóng với các tỉnh lân cận như Biên Hòa ( Đồng Nai), Lâm Đồng, Bình Thuận qua cao tốc Hồ Chí Minh – Long Thành – Dầu Giây
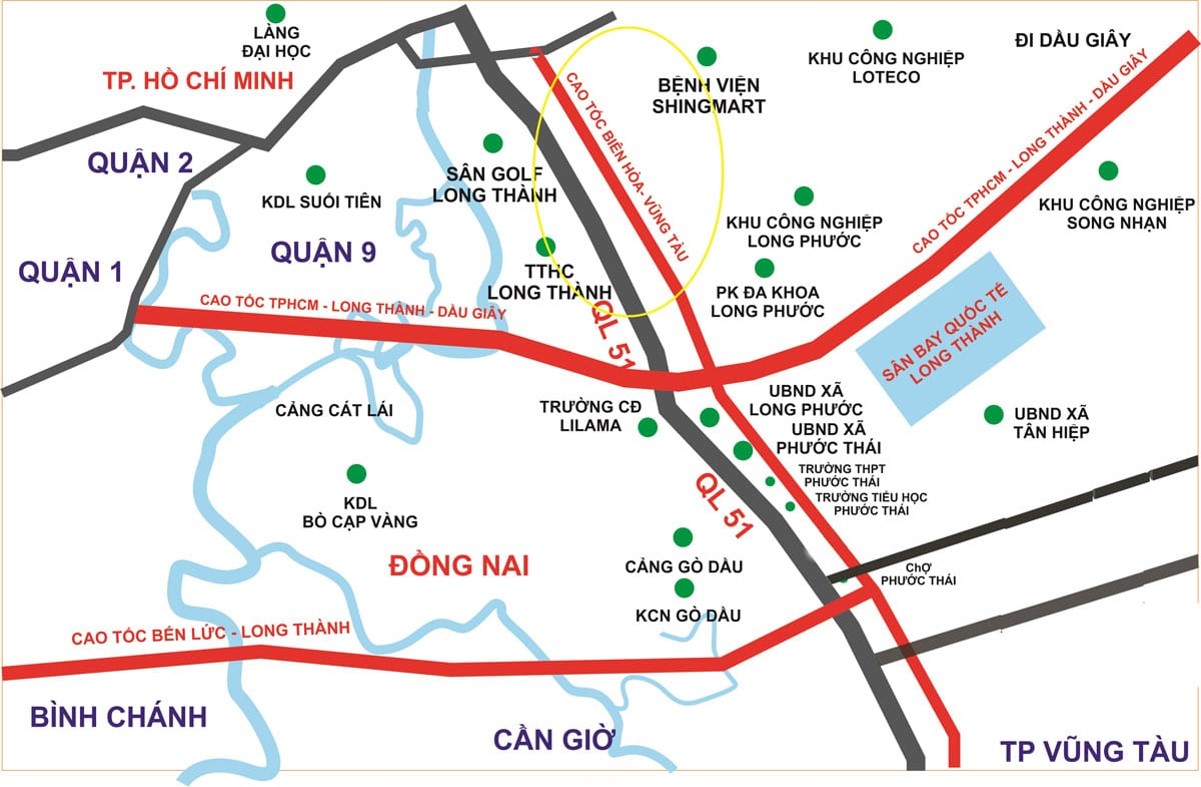
Bên cạnh đó, Tập đoàn tiên phong cho ra mắt thương hiệu xe buýt điện hiện đại Vinbus nhằm rút ngắn thời gian di chuyển đến các khu vực trung tâm như trạm Bến xe MIền Đông, trạm Metro Bến Thành – Suối TiênCơ sở hạ tầng liên tục được đầu tư, mở rộng và nâng cấp
- Nâng cấp và mở rộng tuyến đường Nguyễn Duy Trinh và Đồng Văn Cống kết nối nhanh chóng với quận 9
- Xây dựng tuyến đường Vành Đai 3 kết nối nhanh chóng Hồ Chí Minh – Bình Dương- Đồng Nai – Long An
- Cầu Long Đại kết nối 2 bờ sông khu Long Phước, đường Vành Đai 3 và cao tốc Long Thành – Dầu Giây
Xung quanh dự án là khu dân cư hiện hữu nên dễ dàng tiếp cận tiện ích xung quanh từ trung tâm thương mại, khu vui chơi đến trung tâm hành chính, chợ, trường học…

Tình hình dân số tại các quận trung tâm đang rơi vào tình trạng quá tải nên xu hướng đầu đầu tư đã và đang dịch chuyển về các khu vực vùng ven ngày càng rõ rệt. Thêm vào đó quận 9 lại là nơi đóng đô của các doanh nghiệp quốc tế như Sam Sung, Intel, Microsoft điều này làm gia tăng nhu cầu nhà ở và sử dụng dịch vụ rất lớn. Chính vì thế giá trị bất động sản của quận 9 nói chung và The Manhttan nói riêng trong tương lai sẽ gia tăng nhanh chóng. Đây là cơ hội lý tưởng cho các nhà đầu tư có tầm nhìn chiến lược dài hạn
Được ví như một ốc đảo xanh giữa lòng phố thị khi phân khu nằm liền kề công viên lớn nhất Đông Nam Á được quy hoạch bài bản với bạt ngàn cây xanh và các công viên chủ đề đa sắc màu mang đậm dấu ấn Vinhomes. Không chỉ vậy The Manhattan bùng nổ với chuỗi tiện ích đỉnh cao, hiện đại bậc nhất khu vực kiến tạo chuẩn phong cách sống thượng lưu cho quý cư dân.

Trung tâm thương mại, mua sắm lớn nhất khu vực phía Nam, nơi đây hội tự đầy đủ các mặt hàng từ các thương hiệu đình đám trong và ngoài nước, không gian vui chơi, giải trí sầm uất bậc nhất nước ta. Khu phố thương mại – đường Phong Lan chính là điểm shopping cực chất cho những người có niềm đam mê mua sắm, săn hàng hiệu

Công viên Grand Forest rộng 36ha với 15 cụm công viên chủ đề, điểm nổi bật của toàn bộ dự án. Nơi có khu dã ngoại Sandy Park với bầu không khí trong trẻo, thuần khiết hòa vào những cuộc vui, công viên Olympic Gym với hệ thống máy tập tiên tiến nhất được rải khắp khuôn viên mang đến cảm giác lý thú khi tập luyện. Bung xõa hết mình với sông nước tại khu chèo thuyền Kayak, đặc biệt công viên Ánh Sáng rực rỡ sắc màu, kiêu hãnh thắp sáng cả bầu trời Quận 9

Thả mình dưới làn nước mát trong xanh, tạm gác lại những âu lo phiền muộn của cuộc sống thường nhật tại hồ bơi tràn bờ. Hay làm nóng cơ thể, vận động cơ bắp qua những hoạt động sôi nổi tại khu thể dục thể thao trong nhà và ngoài trời với đầy đủ các bộ môn yoga, tennis, cầu lông…

Hệ thống an ninh chặt chẽ, hoạt động 24/24 cùng đơn vị quản lý & vận hành tiêu chuẩn Vinhomes kết hợp ứng dụng công nghệ 4.0 và Face ID nhận diện khuôn mặt mang đến sự an toàn, tiện nghi mà vẫn bảo đảm quyền riêng tư cho quý cư dânPhát triển tài năng, ươm mầm thế hệ tương lai tươi sáng cho cư dân nhí tại hệ thống trường học liên cấp Vinschool, khu vui chơi với đa dạng các hoạt động giúp trau dồi cảm xúc lẫn trí tuệ cho các em…

Như đã trình bày ở phần thế mạnh vị trí, tiện ích ngoại khu The Manhattan vô cùng đa dạng từ khu vui chơi, giải trí đến hệ thống trường học, bệnh viện, trung tâm hành chính… tất cả được kết nối vô cùng dễ dàng.
Dự án The Manhattan có tổng quy mô 550 căn với đa dạng các loại hình sản phẩm và diện tích phù hợp nhu cầu và tài chính của khách hàng.
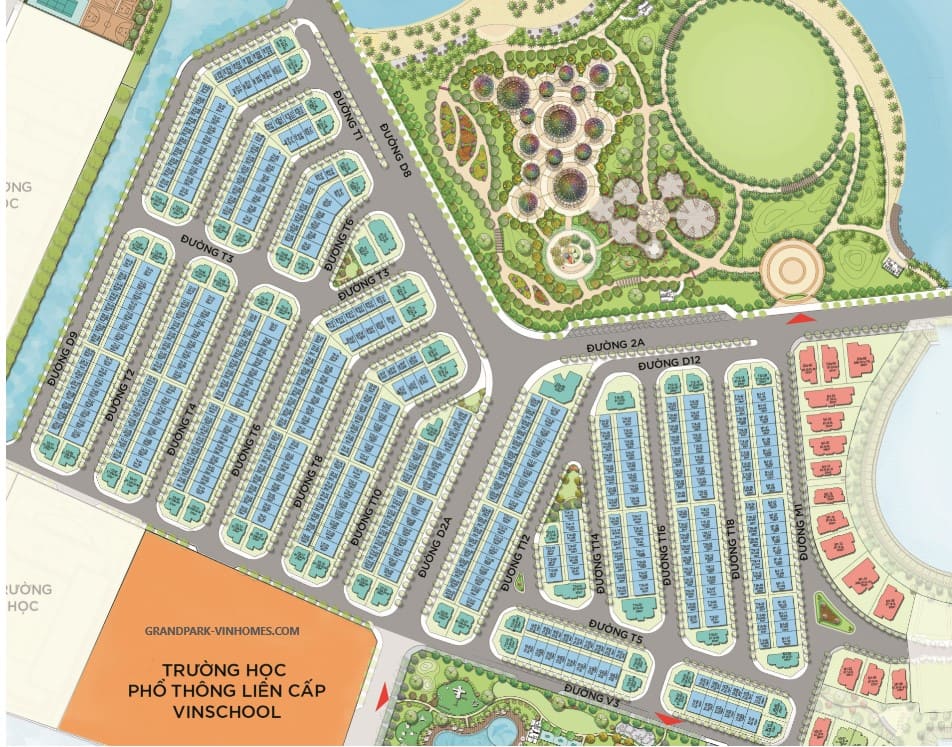


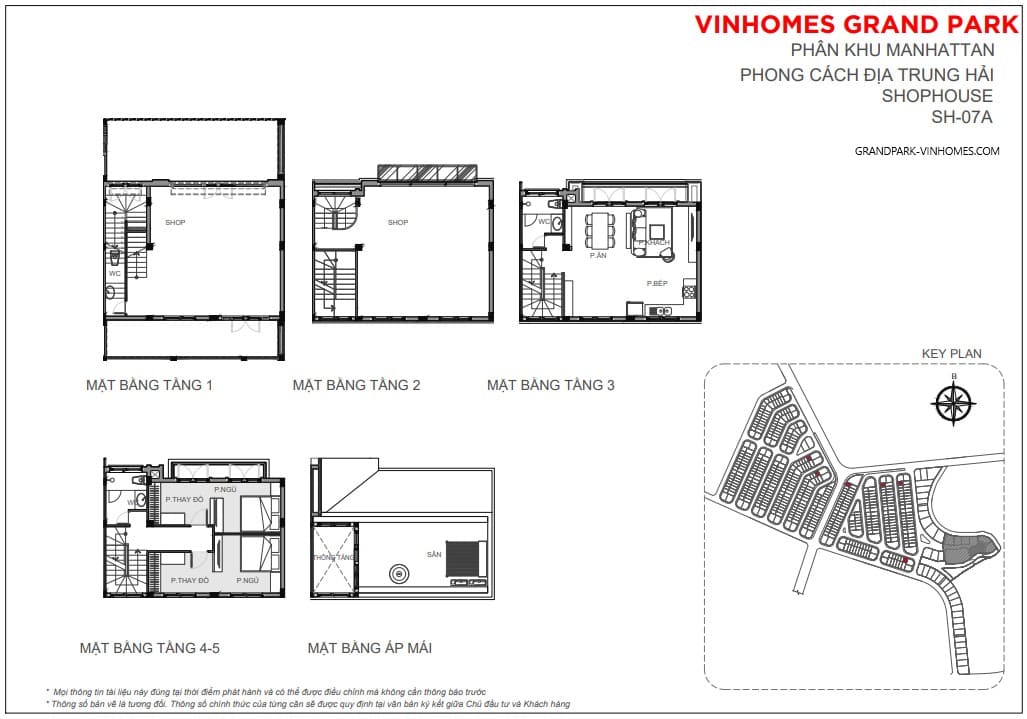
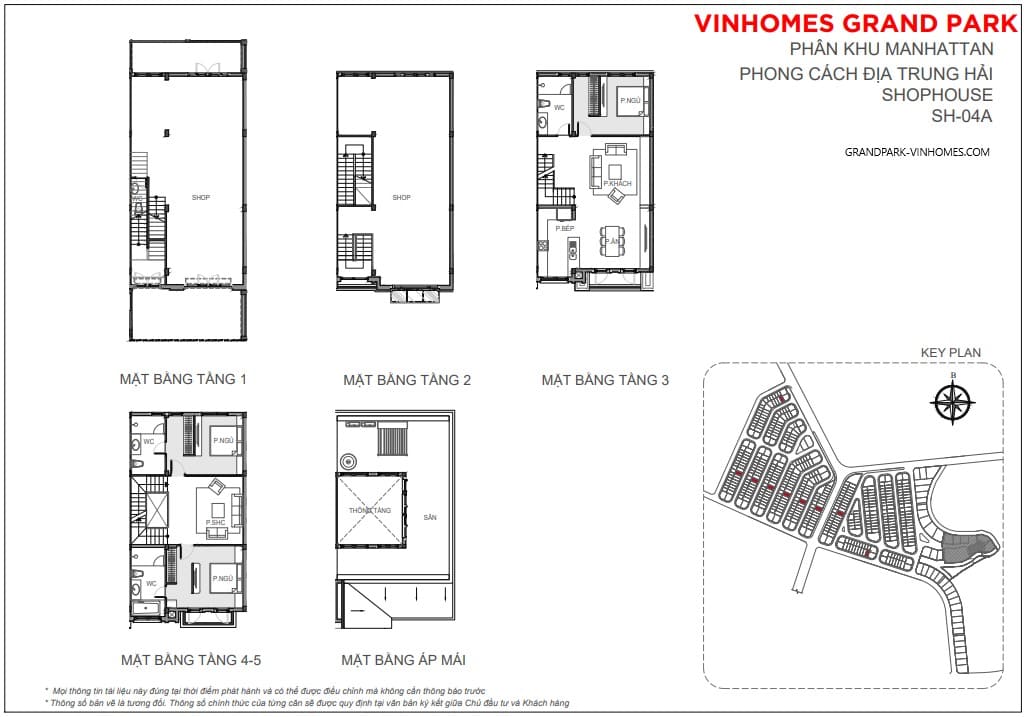
 Shophouse được xây dựng 5 tầng gồm 1 trệt, 4 lầu diện tích đất xây dựng dao động từ 84 – 230m2 và diện tích sàn xây dựng từ 180 – 720m2
Shophouse được xây dựng 5 tầng gồm 1 trệt, 4 lầu diện tích đất xây dựng dao động từ 84 – 230m2 và diện tích sàn xây dựng từ 180 – 720m2
 Boutique Villa với quy mô 1 trệt, 2 lầu diện tích đất dao động từ 170 m2, diện tích sàn xây dựng từ 200 – 880m2
Boutique Villa với quy mô 1 trệt, 2 lầu diện tích đất dao động từ 170 m2, diện tích sàn xây dựng từ 200 – 880m2
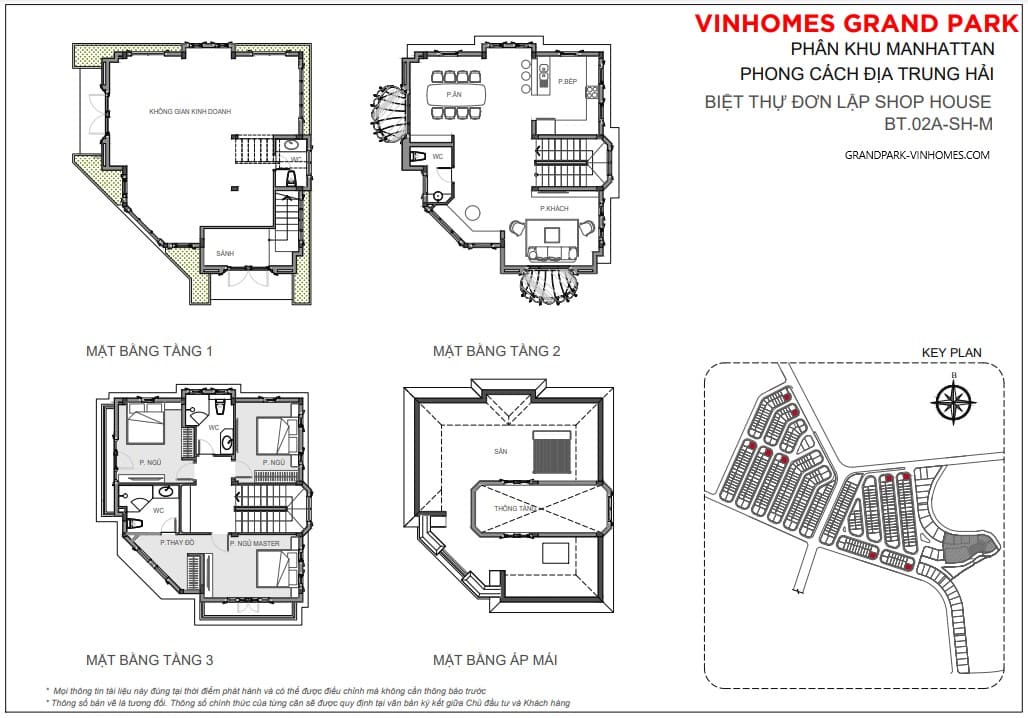
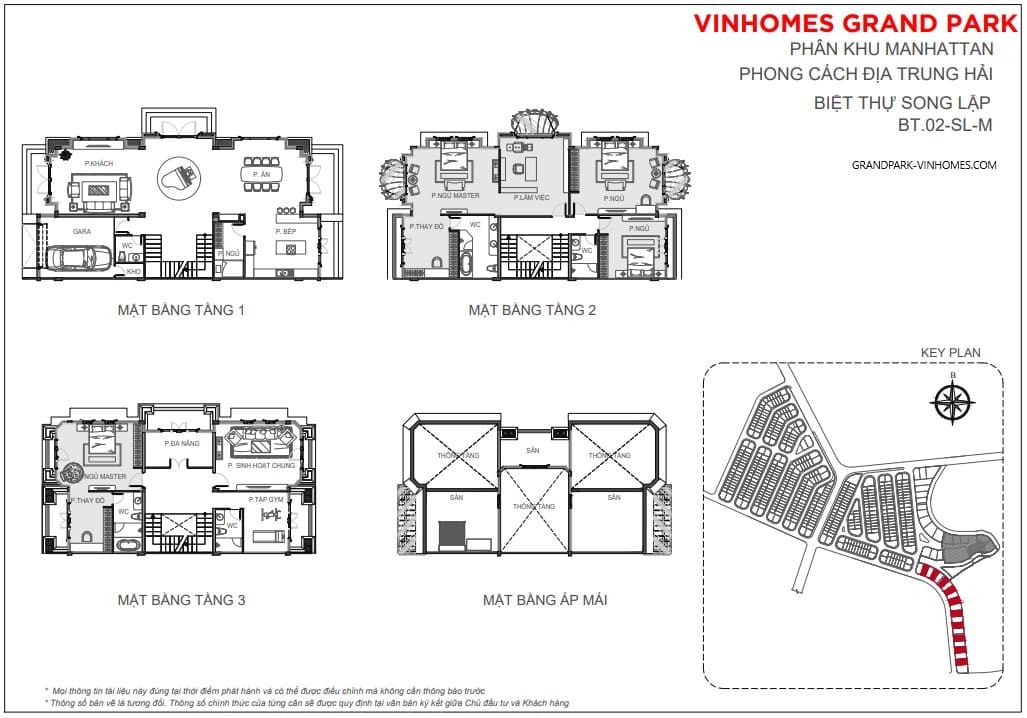
Khu biệt thự Riverside Villa được chia làm 2 loại đó là biệt thự đơn lập và biệt thự song lập trong đó:
- Biệt thự đơn lập có quy mô 3 tầng với 1 trệt, 2 lầu diện tích xây dựng dao dộng 310m2 – 800m2, diện tích mặt sàn xây dựng là 420m2 – 850m2
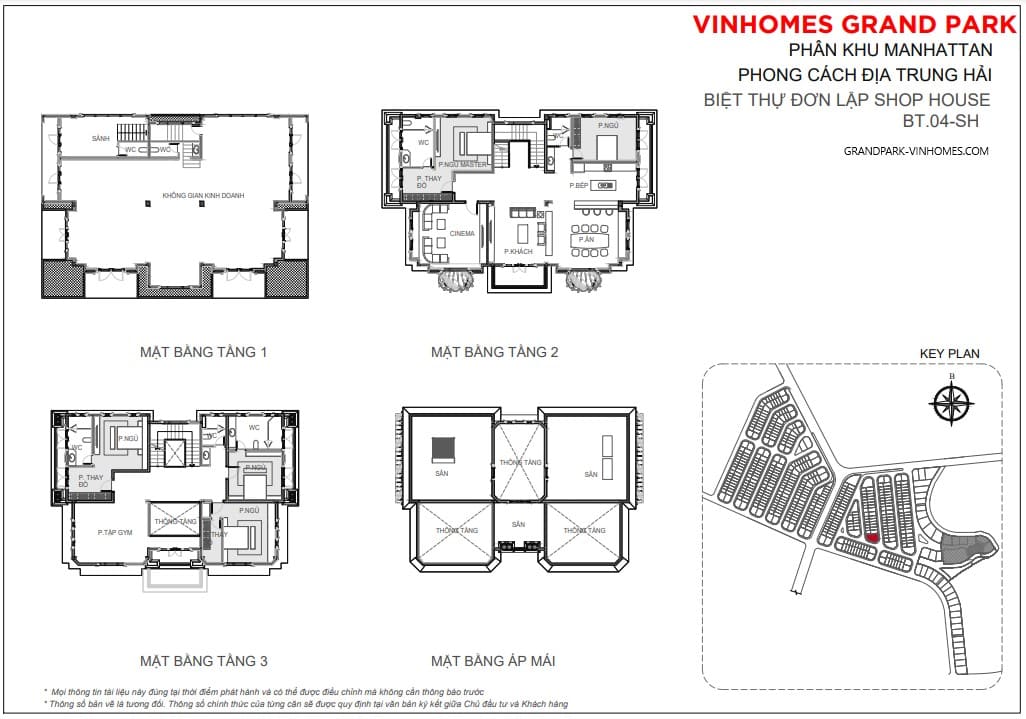
- Biệt thự song lập có 3 tầng với 1 trệt, 2 lầu diện tích đất xây dựng dao dộng 340m2 – 560m2, diện tích mặt sàn xây dựng là 510m2 – 540m2
Các sản phẩm tại The Manhattan được “đo ni đóng giày” dành riêng cho nhóm khách hàng tinh hoa vì vậy không ngạc nhiện khi phong cách thiết kế vô cùng sang trọng và đẳng cấp.Các căn shophouse và Boutique villa tại phân khu mang đến cái nhìn mới mẻ về mô hình kinh doanh kết hợp với nhà ở. Nơi đây khoác lên mình lối kiến trúc đậm dấu ấn Địa Trung Hải hòa quyện cùng lối kiến trúc Gothic..Từng sản phẩm đem lại cảm giác thật xa hoa và lộng lẫy
Các căn Riverside Villas được thiết kế đậm phong cách Đông Dương toát lên vẻ đẹp cuốn hút mê hoặc lòng người, nổi bật là những hình khối tinh tế mang nét đặc trưng của miền Bắc nước Pháp. Từ mái ngói đến khung cửa, những đường nét được khắc họa cực kỳ sắc sảo…tất cả tạo nên những căn biệt thự ven sông với nhiều layout đẹp tuyệt hảo không thể rời mẳt
Giá bán và Phương thức thanh toán
The Manhattan có mức giá cực kỳ hấp dẫn, phù hợp với nhu cầu và khả năng tài chính của nhiều nhóm khách hàng
| Loại căn hộ | Diện tích (m2) | Giá bán (dự kiến) |
| Nhà phố | 84 – 230 | Từ 13 tỷ |
| Shop villa | 178 – 678 | Từ 27 tỷ |
| Biệt thự đơn lập | 346 – 442 | Từ 40 tỷ |
| Biệt thự song lập | 314 – 805 | Từ 37 tỷ |
Phương thức thanh toán
| Đợt | Thời gian | Tỉ lệ thanh toán |
| Đặt cọc | 50 triệu đồng khi ký thỏa thuận đặt cọc | |
| Đợt 1 | Sau 07 ngày từ khi ký TTĐC | 15% (Bao gồm 50 triệu đặt cọc) và tiến hành ký HĐMB |
| Đợt 2 | 22 ngày từ ngày ký TTĐC | Ngân hàng giải ngân 70% |
| Đợt 3 | 79 ngày từ ngày ký TTĐC | 5% |
| Đợt 4 | 139 ngày từ ngày ký TTĐC | 10% |
Chủ đầu tư đã ký hợp đồng chiến lược với ngân hàng Techcombank để hỗ trợ vay vốn khi mua các sản phẩm tại The Manhattan. Khách hàng được hỗ trợ 70% giá trị hợp đồng và hỗ trợ lãi suất lên đến 18 tháng, phí trả nợ trước hạn 0% trong thời gian hỗ trợ lãi suất và ân hạn gốc 18 thángNếu khách hàng không có nhu cầu vay vốn ngân hàng và thanh toán trong vòng 15 ngày kể từ ngày ký hợp đồng mua bán sẽ được chiết khấu như sau
- Người Việt Nam: thanh toán 95% chiết khấu 9% vào giá bán
- Người nước ngoài: thanh toán 70% chiếu khấu 6% vào giá bán
Phân khu The Origami - Dự án Vinhomes Grand Park
The Origami
The Origami là một trong những phân khu độc đáo của dự án Vinhome Grand Park được tọa lạc tại Nguyễn Xiển, phường Long Thạnh Mỹ, thành phố Thủ Đức, thành phố Hồ Chí Minh do Tập đoàn Vingroup làm chủ đầu tư. Được quy hoạch theo mô hình đô thị thông minh khép kín theo tiêu chuẩn quốc tế, đồng bộ về hạ tầng , chuỗi tiện ích hiện đại đã góp phần kiến tạo nên khu đại đô thị thời thượng, đẳng cấp bậc nhất tại khu vực mở ra không gian sống thịnh vượng, hạnh phúc như chính tên gọi của nó.

|
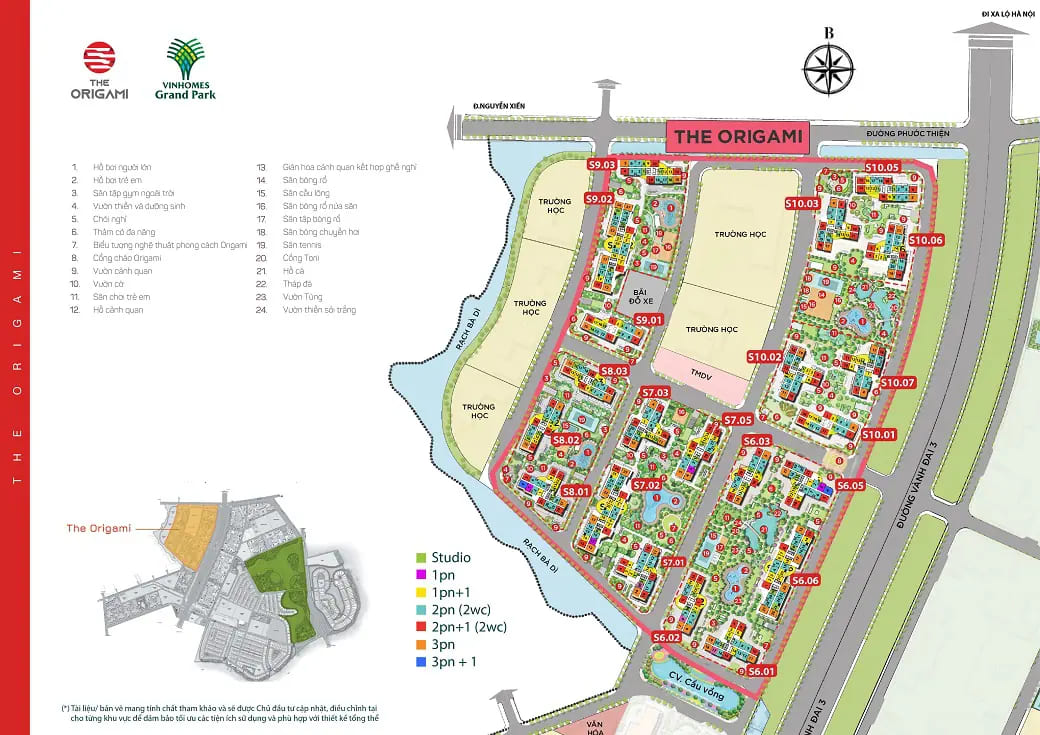
PHÂN KHU THE ORIGAMI – Tên thương mại: Phân khu The Origami.– Quy mô: 21 tòa, hơn 12.000 căn hộ.– Chiều cao: 21 – 30 tầng.– Diện tích căn hộ: từ 29m2 – 108m2.– Giá bán: từ 45 – 60 triệu/m2.– Thời gian bàn giao dự kiến: S6, S7, S8, S9 bàn giao Quý 1/2023. S10 bàn giao Quý 4/2023 CHÍNH SÁCH ƯU ĐÃI – PHÂN KHU THE ORIGAMI – Tặng Voucher Vinfast trị giá 70 – 150 – 200 triệu/căn– Tặng gói nội thất trị giá: 100 triệu căn 1PN, 130 triệu căn 1PN+, 180 triệu căn 2PN, 200 triệu căn 2PN+, 250 triệu căn 3PN– Chiết khấu đến 8% khi thanh toán chuẩn (không vay)– Ân hạn gốc & lãi 0% từ 12 – 18 tháng cho gói vay 80 – 100% giá bán |
 |
| STUDIO | 1 PN | 2 PN | 3 PN |
| 34m² | 46,5m² – 47,2m² | 59m² – 69m² | 82m² |
| Cho thuê: 3,8 Triệu/tháng | Cho thuê: 4,5 Triệu/tháng | Cho thuê: 5 Triệu/tháng | Cho thuê: 6 Triệu/tháng |
| Giá bán: 1,1 – 2 Tỷ | Giá bán: từ 1.5 tỷ | Giá bán: từ 2 tỷ | Giá bán: từ 2,5 tỷ |

Tổng quan dự án The Origami
|
 |
The Origami tọa lạc tại đường Nguyễn Xiển, phường Long Thạnh Mỹ, thành phố Thủ Đức, thành phố Hồ Chí Minh. Nằm liền kề phân khu The Rainbow và đường Vành Đai 3 tạo điều kiện thuận lợi trong việc di chuyển trong nội khu cũng như về trung tâm thành phố
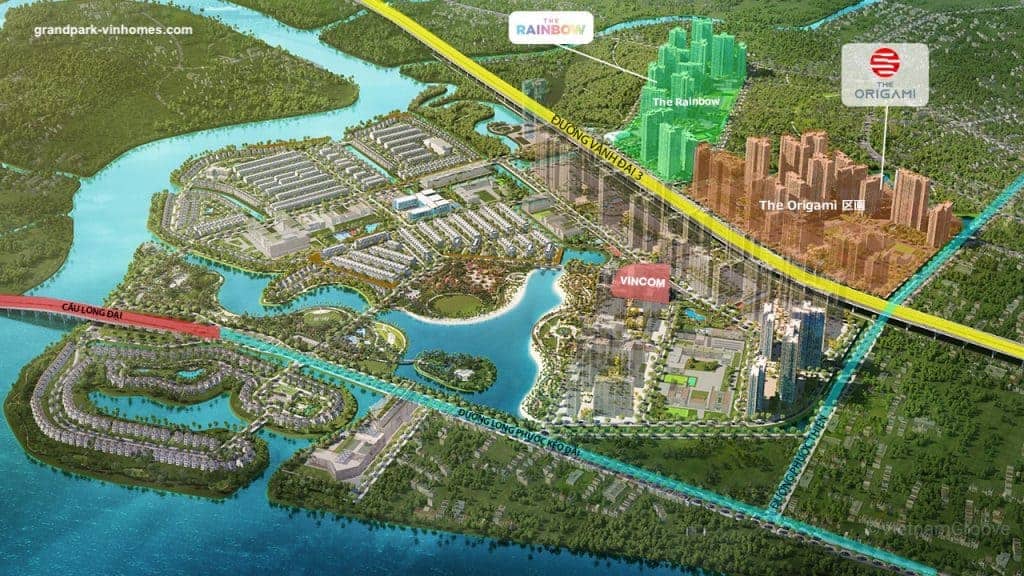
Bốn phía của phân khu tiếp giáp các khu vực trọng điểm
- Phía Đông: liền kề với phân khu 3, công viên Grand Park 36ha, Vincom Mega Mall và kết nối tuyến giao thông Vành Đai 3 trên cao đi ngang qua dự án
- Phía Tây: khu dân cư hiện hữu
- Phía Nam: hướng về Sông Tắc, liền kề phân khu The Rainbow
- Phía Bắc: liền kề khu dân cư Phước Thiện
Không chỉ sở hữu địa thế phong thủy cực thịnh trong giới bất động sản với đầy đủ 3 tiêu chí “nhất cận thị, nhị cận giang, tam cận lộ mang đến môi trường sống lý tưởng cho cộng đồng dân cư mà còn có cơ sở hạ tầng liên tục được đầu tư và nâng cấp

- Xây dựng tuyến Vành Đai 3 với mức vốn siêu khủng giúp kết nối nhanh chóng Hồ Chí Minh – Bình Dương- Đồng Nai – Long An
- Nâng cấp và mở rộng tuyến đường Nguyễn Duy Trinh và Đồng Văn Cống kết nối trực tiếp với quận 9…
- Cầu Long Đại cây cầu chiến lược giúp kết nối 2 bờ sông khu Long Phước, đường Vành Đai 3 và cao tốc Long Thành – Dầu Giây
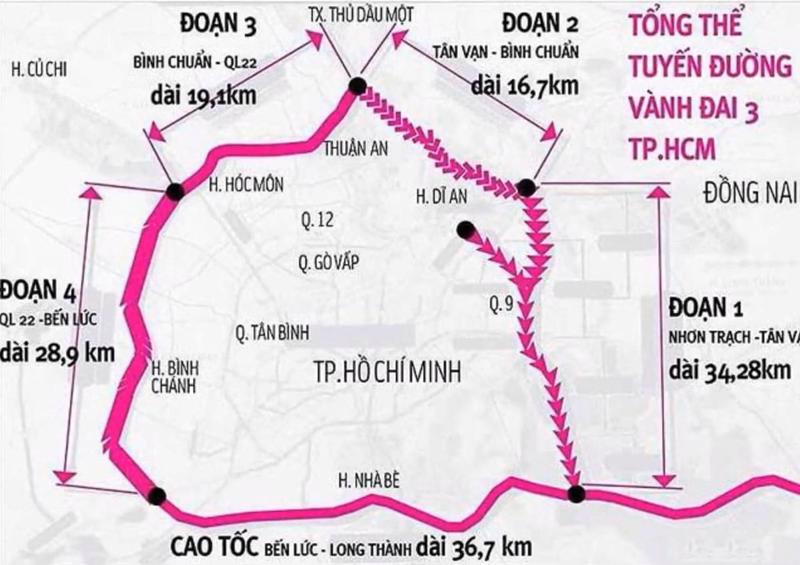
Bên cạnh đó, Tập đoàn Vingroup tiên phong ra mắt thương hiệu xe buýt điện Vinbus đưa cư dân đến các khu vực trung tâm như trạm Metro Bến Thành – Suối Tiên, Trạm bến xe Miền Đông nhanh chóng.Quận 9 là nơi thu hút hàng tỷ USD đầu tư của nhiều doanh nghiệp quốc tế như Intel, Microsoft, Samsung..tại khu công nghệ cao 1 và 2. Điều này làm gia tăng nhu cầu nhà ở và sử dụng các dịch vụ rất lớn. Thêm vào đó, với tình hình dân số tại các quận trung tâm đang rơi vào tình trạng quá tải nên xu hướng đầu tư đã và đang dịch chuyển về các khu vực vùng ven. Nhờ đó mà giá trị bất động sản nơi đây tăng vọt, cơ hội sinh lời lý tưởng cho các nhà đầu tư có tầm nhìn chiến lược lâu dài.
Tiện ích nội khu dự án The Origami
The Origami được tích hợp tiện ích hiện đại quy hoạch theo mô hình “All in one” kết hợp phong cách sống mang đậm dấu ấn của tinh hoa xứ sở hoa anh đào Nhật Bản mang đến những trải nghiệm độc đáo và mới mẻ cho cư dân sinh sống tại đâyThong dong sải bước trên con đường rộng rãi, thông thoáng lắng nghe những thanh âm trong trẻo bên tai, tận hưởng làn gió tươi mát khẽ lướt qua cho bạn cảm giác yên bình trong những buổi chiều mát mẻ tại công viên và đường đi bộ nội khu

Trung tâm thương mại sôi động với các dịch vụ đa dạng, sang chảnh cùng chuỗi các nhà hàng, quán café với đầy đủ các món ăn, thức uống đặc sắcPhát triển tài năng, ươm mầm tương lai cho cư dân nhí tại hệ thống trường học Vinschool, khu vui chơi với các hoạt động thú vị nơi khám phá những điều kỳ diệu, những niềm vui bất tận của trẻ thơ

Đập tan mọi ưu phiền, lắng lo của cuộc sống ta đắm chìm vào làn nước mát lành, trong xanh sau những giờ luyện tập thể thao miệt mài nâng cao sức khỏe tại sân thể thao ngoài trời rộng lớn

Phòng tập gym với trang thiết bị hiện đại, tiên tiến bậc nhất cùng các huấn luyện viên nhiệt tình, sẵn sàng hỗ trợ cho quý cư dân trong suốt quá trình tập luyện. Ngoài ra còn vô vàn tiện ích hiện hữu trong nội khu như hệ thống bệnh viện, spa, hệ thống camera…

Tiện ích ngoại khu The Origami cực kỳ đa dạng từ khu vui chơi, giải trí đến hệ thống trường học, trung tâm hành chính… tất cả được kết nối rất dễ dàng nhanh chóng

Dự án The Origami có tổng quy mô 21 tòa căn hộ cao 25 -35 tầng, 2 tầng hầm gồm 10.000 căn hộ cao cấp 1 – 3PN có diện tích từ 33m2 – 89m2 nhằm giúp khách hàng có nhiều sự lựa chọn phù hợp với nhu cầu và tài chính của mình
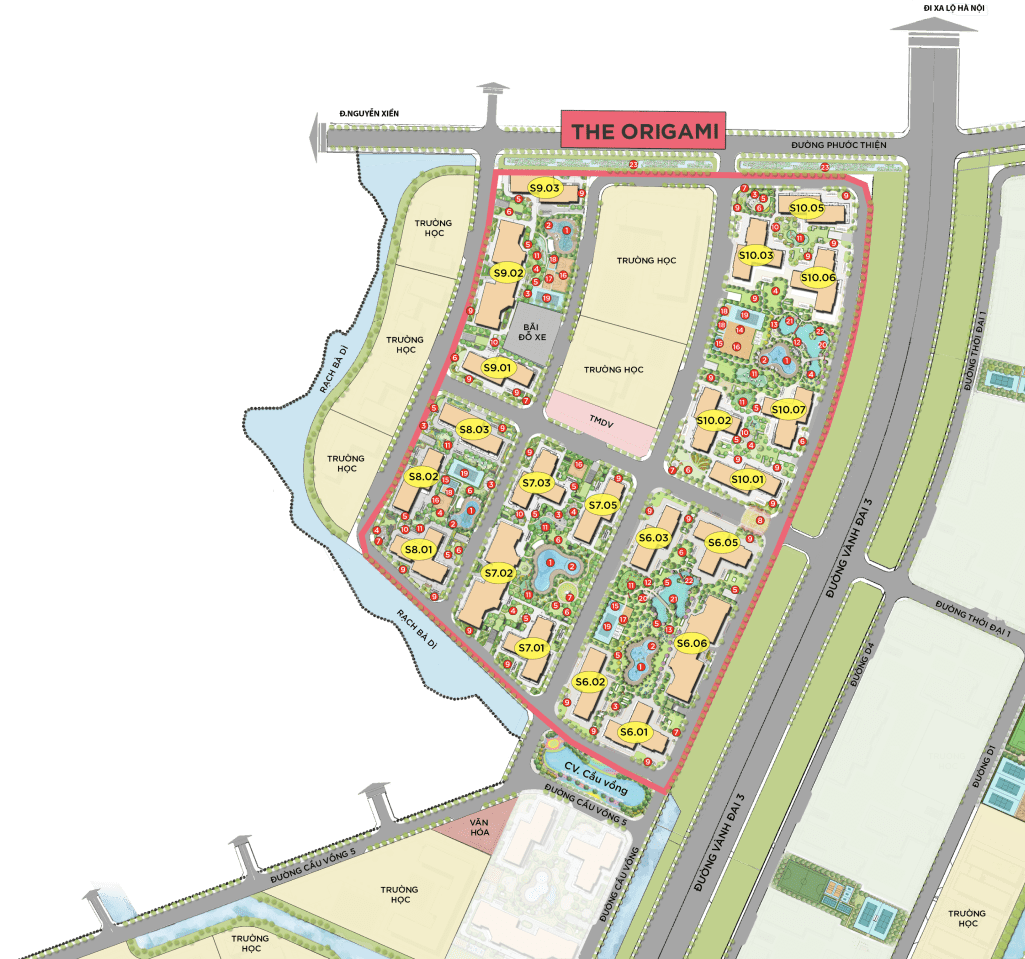
- Căn hộ Studio có diện tích 27 – 39m2
- Căn hộ 1PN có diện tích 36.4 – 51.8m2
- Căn hộ 2PN có diện tích 58.3 – 70.4m2
- Căn hộ 3PN có diện tích 80 – 108m2
Các tầng được thiết kế với 3 mặt bằng khác nhau: Tòa chữ T, Tòa chữ Z, Tòa chữ U. Mỗi tòa đều có 4 đến 10 thang máy, hành lang căn hộ rộng 1.6m thông gió tự nhiên, không có điều hòaMặt bằng tòa chữ T cao từ 34 – 45 tầng, tổng số lượng trên sàn là 21 cănMặt bằng tòa chữ Z cao từ 25 – 26 tầng, tổng số lượng căn hộ trên sàn là 19 cănMặt bằng tòa chữ U cao từ 34 – 36 tầng, tổng số lượng căn hộ trên sàn là 30 căn

Chủ đầu tư đã dành phần lớn diện tích làm cảnh quan xung quanh, tiện ích nội khu, hạ tầng kỹ thuật…tạo ra không gian thông thoáng, trong lành.Mỗi căn hộ có cửa sổ thông thoáng, ban công rộng rãi hưởng trọn ánh sáng và gió tự nhiên mang lại vượng khí tài lộc cho gia chủ.Lối kiến trúc được quy hoạch đồng bộ với những đường nét sắc sảo, tinh tế kết hợp với những gam màu trang nhã mang đến vẻ ngoài sang trọng,đẳng cấp cho căn hộ. Tận dụng tối đa công năng và diện tích của căn nhà, mở ra không gian sống thời thượng, xứng tầm với vị thế của những chủ nhân tương lai
CHI TIẾT CÁC TOÀ TẠI PHÂN KHU THE ORIGAMI
TÒA S6.01
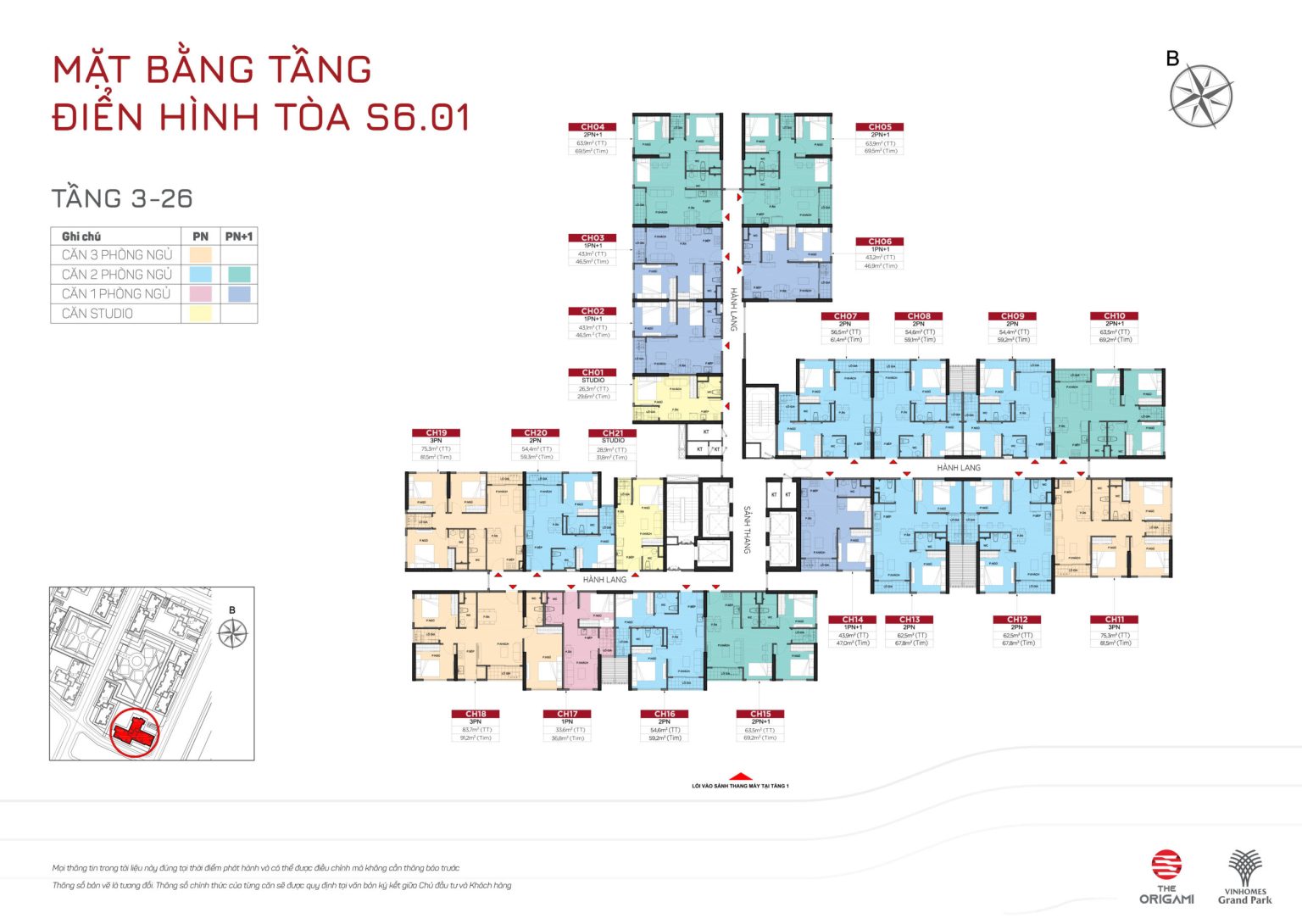
TÒA S6.02
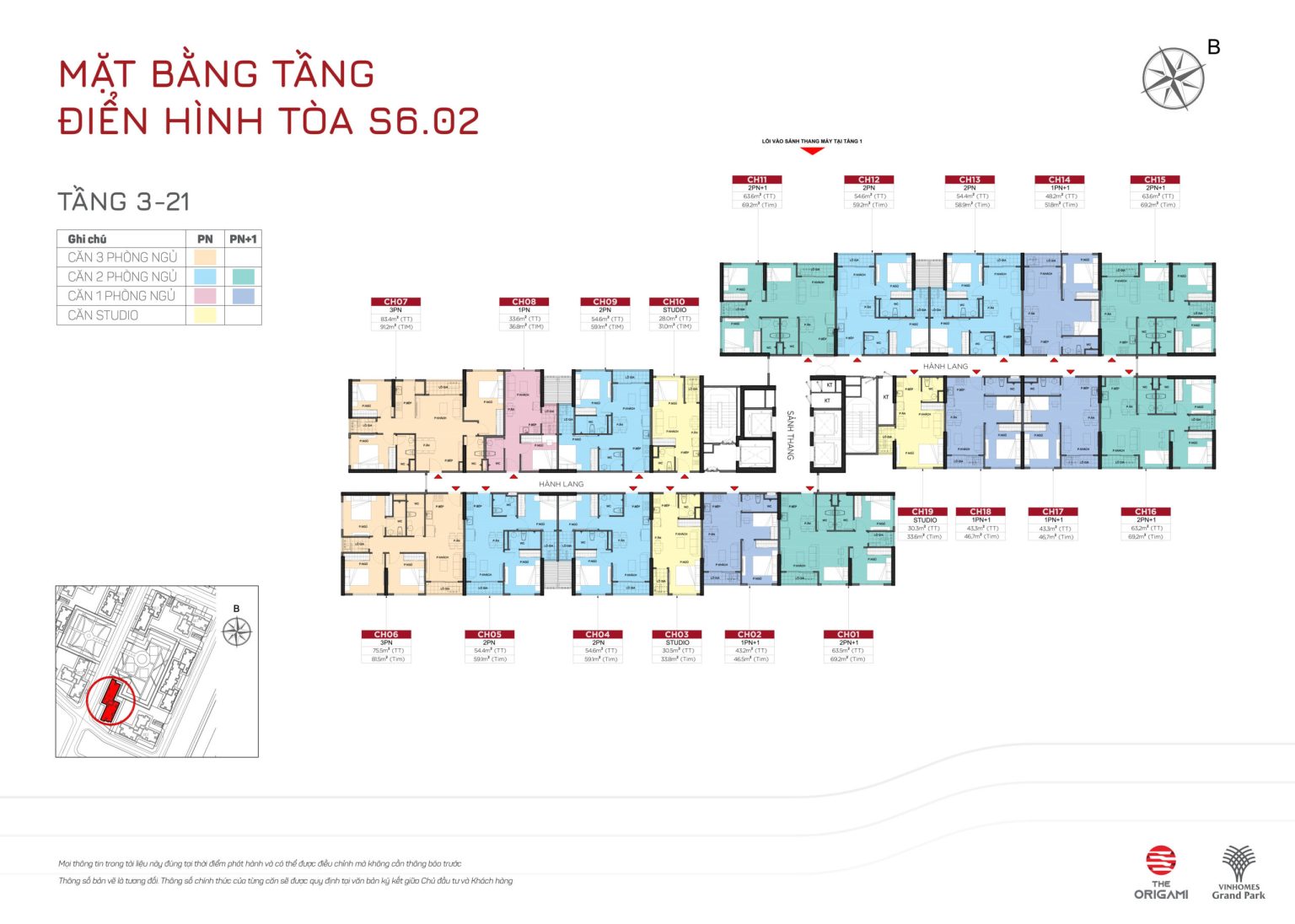
TÒA S6.03
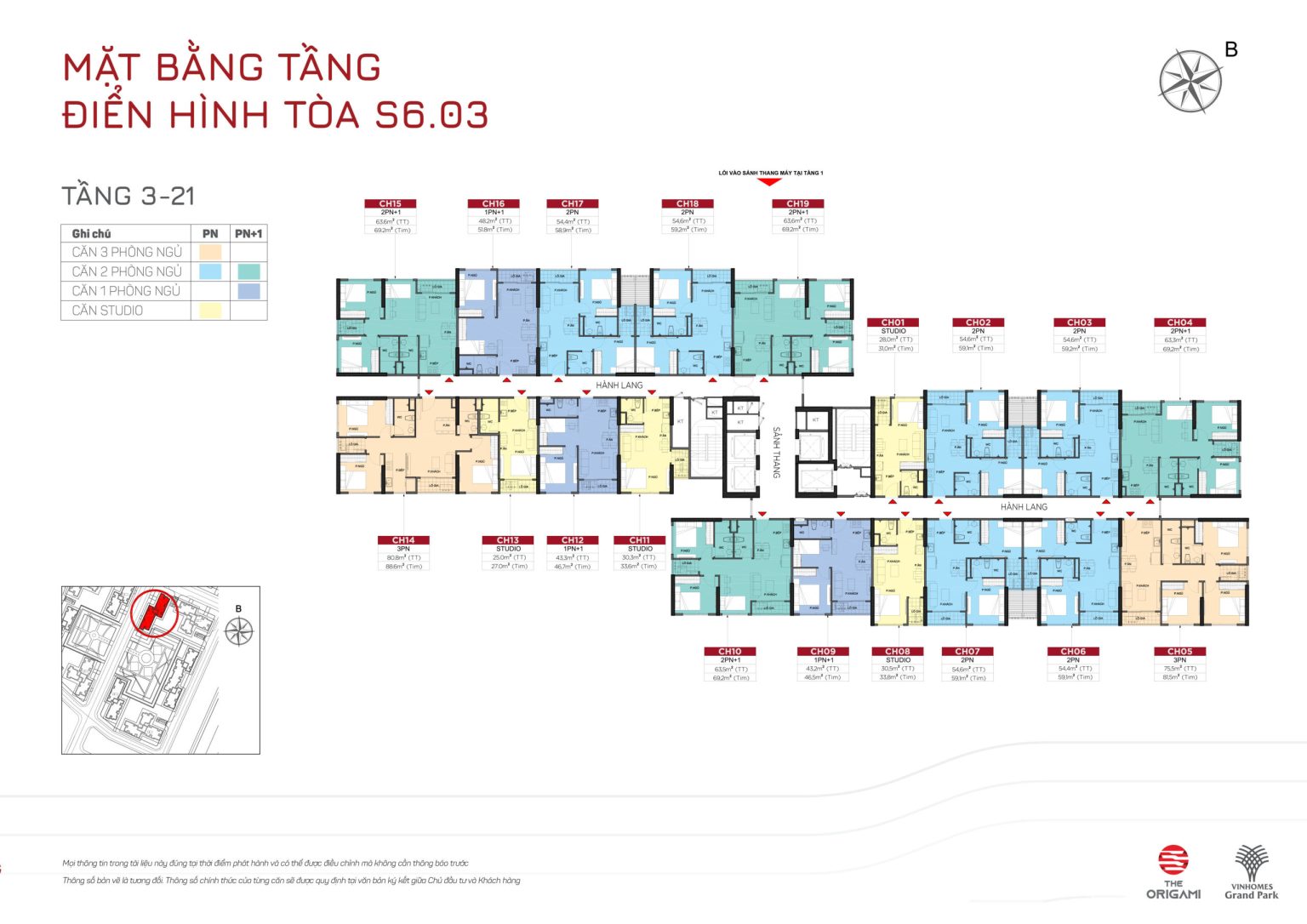
TÒA S6.05
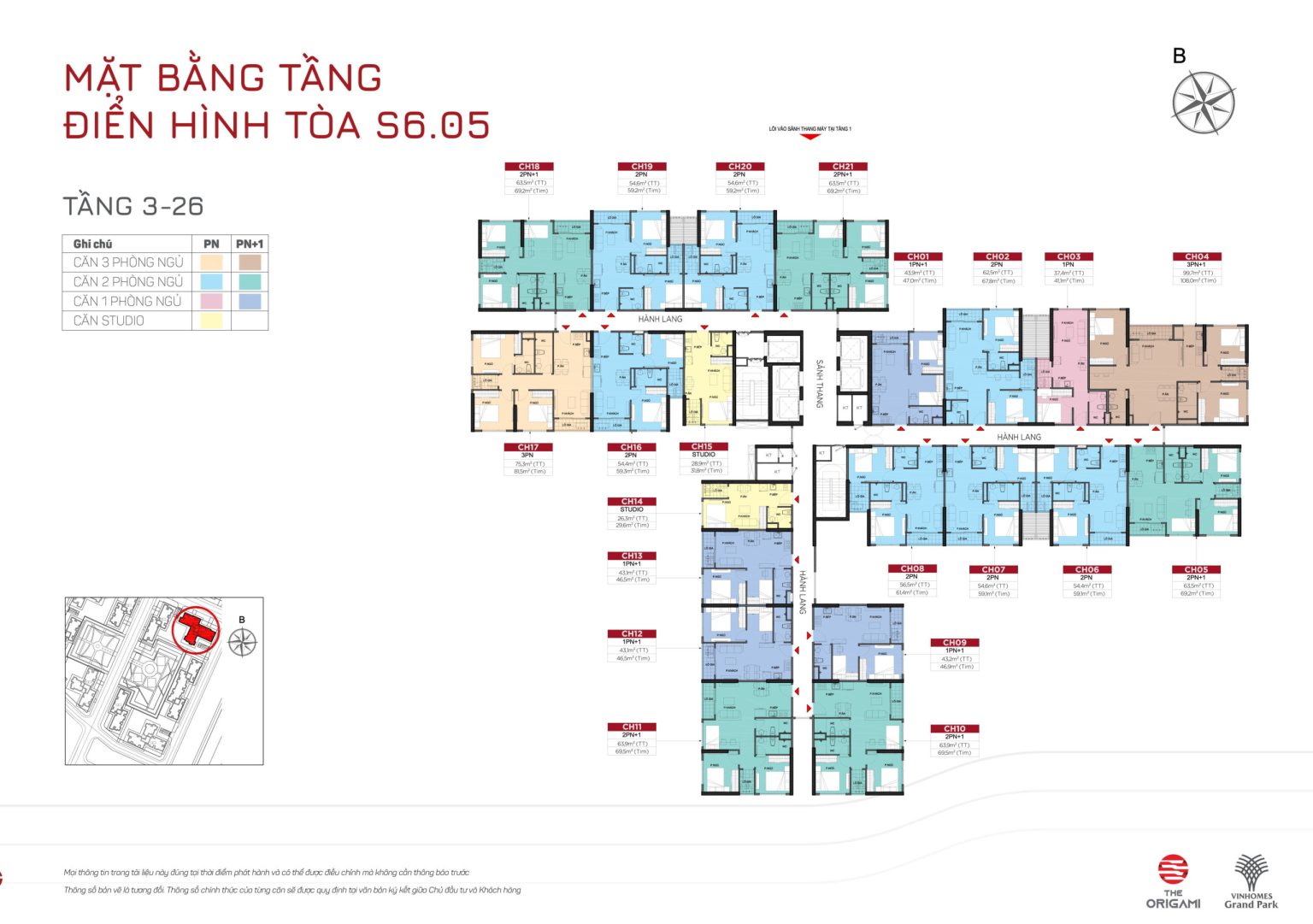
TÒA S6.06
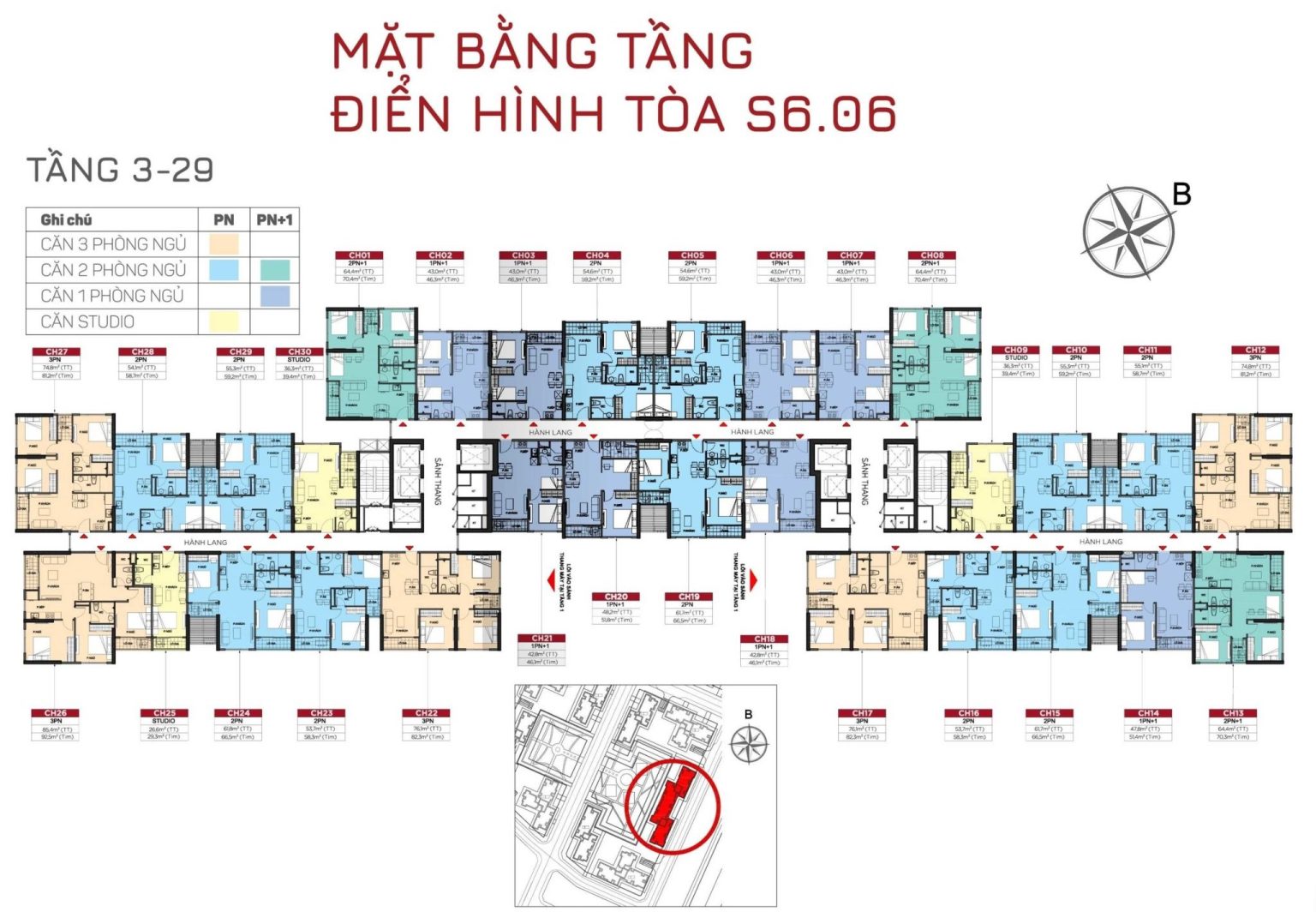
TÒA S7.01
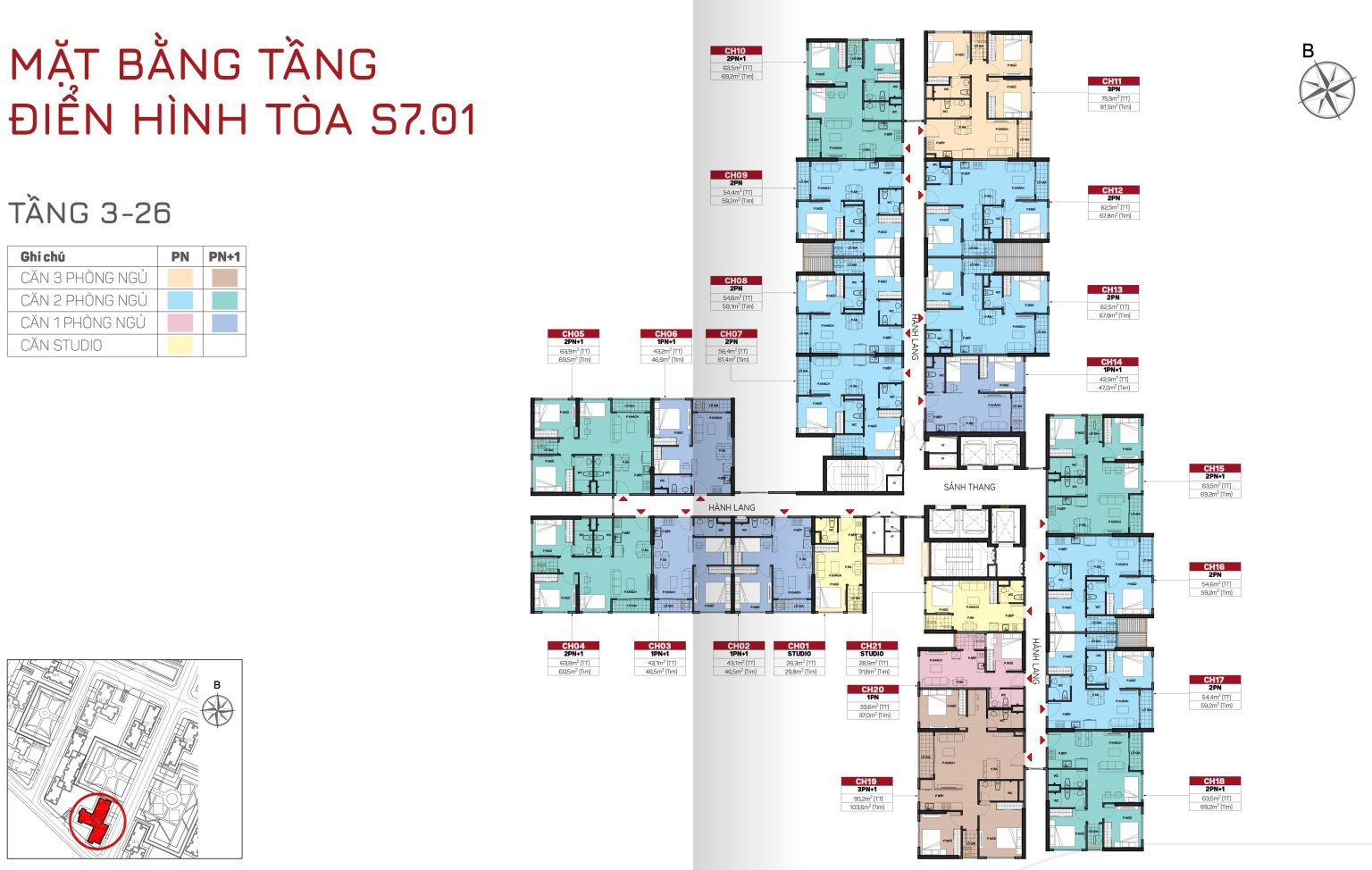
TÒA S7.02
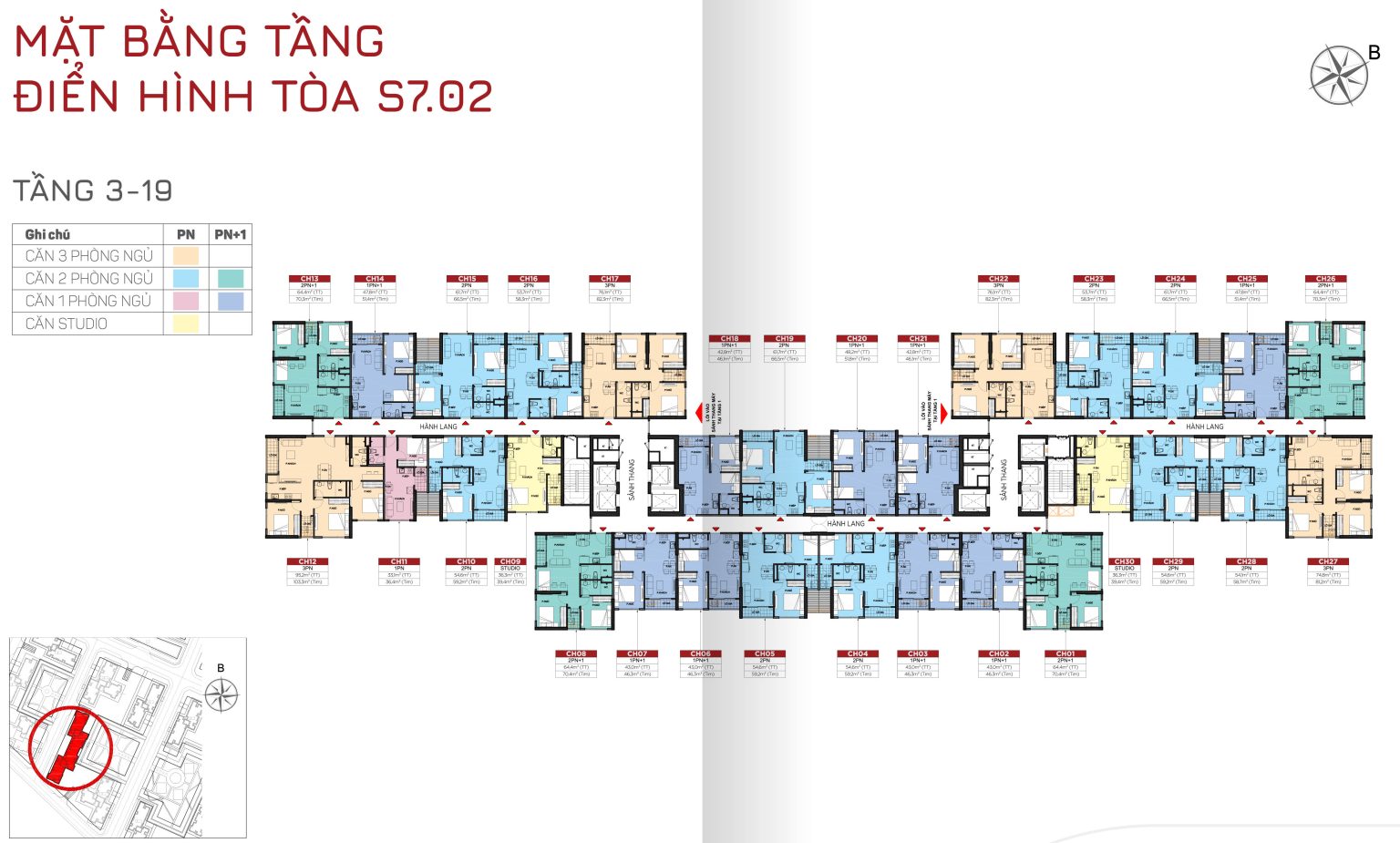
TÒA S7.03
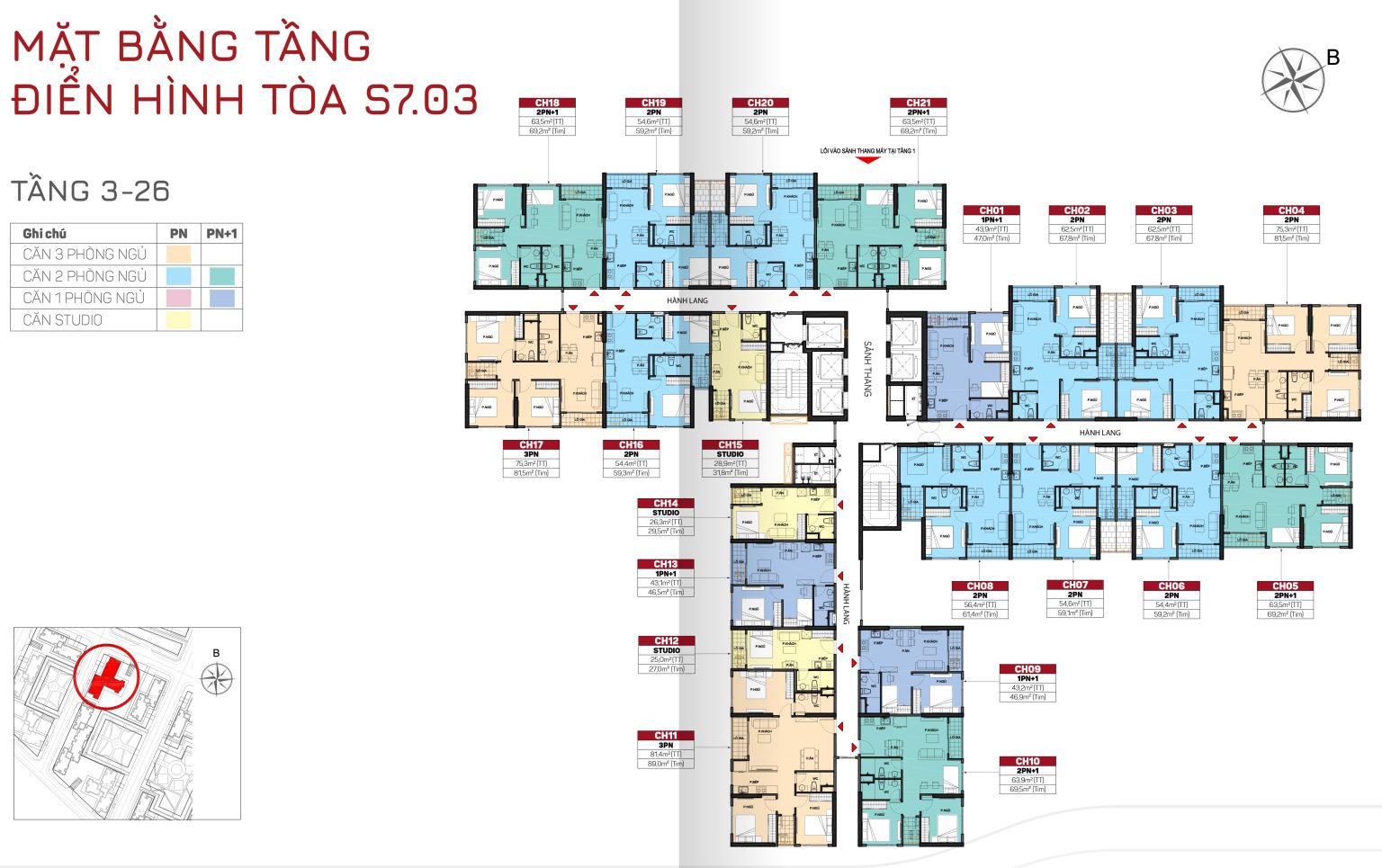
TÒA S7.05
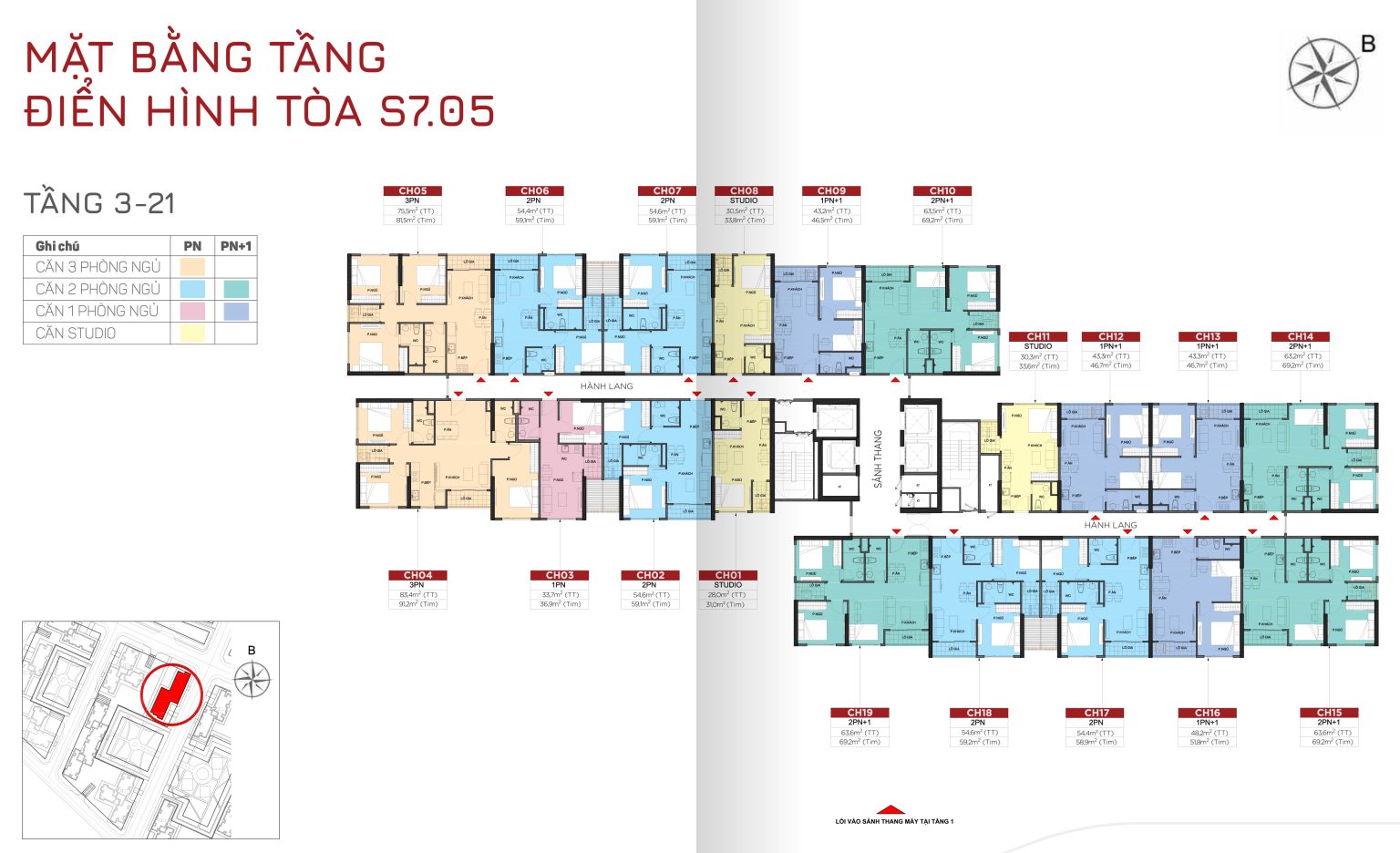
TÒA S8.01
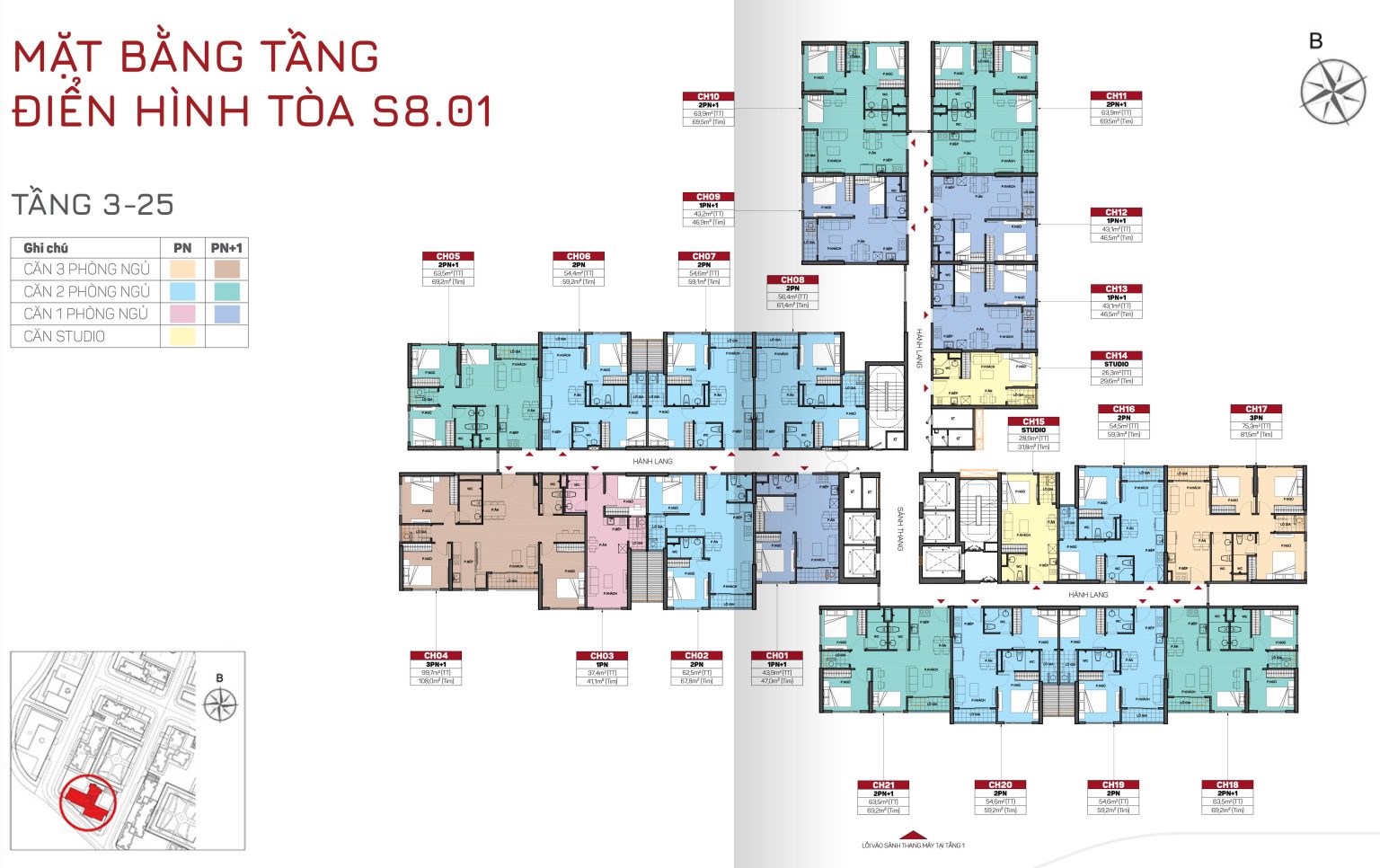
TÒA S8.02
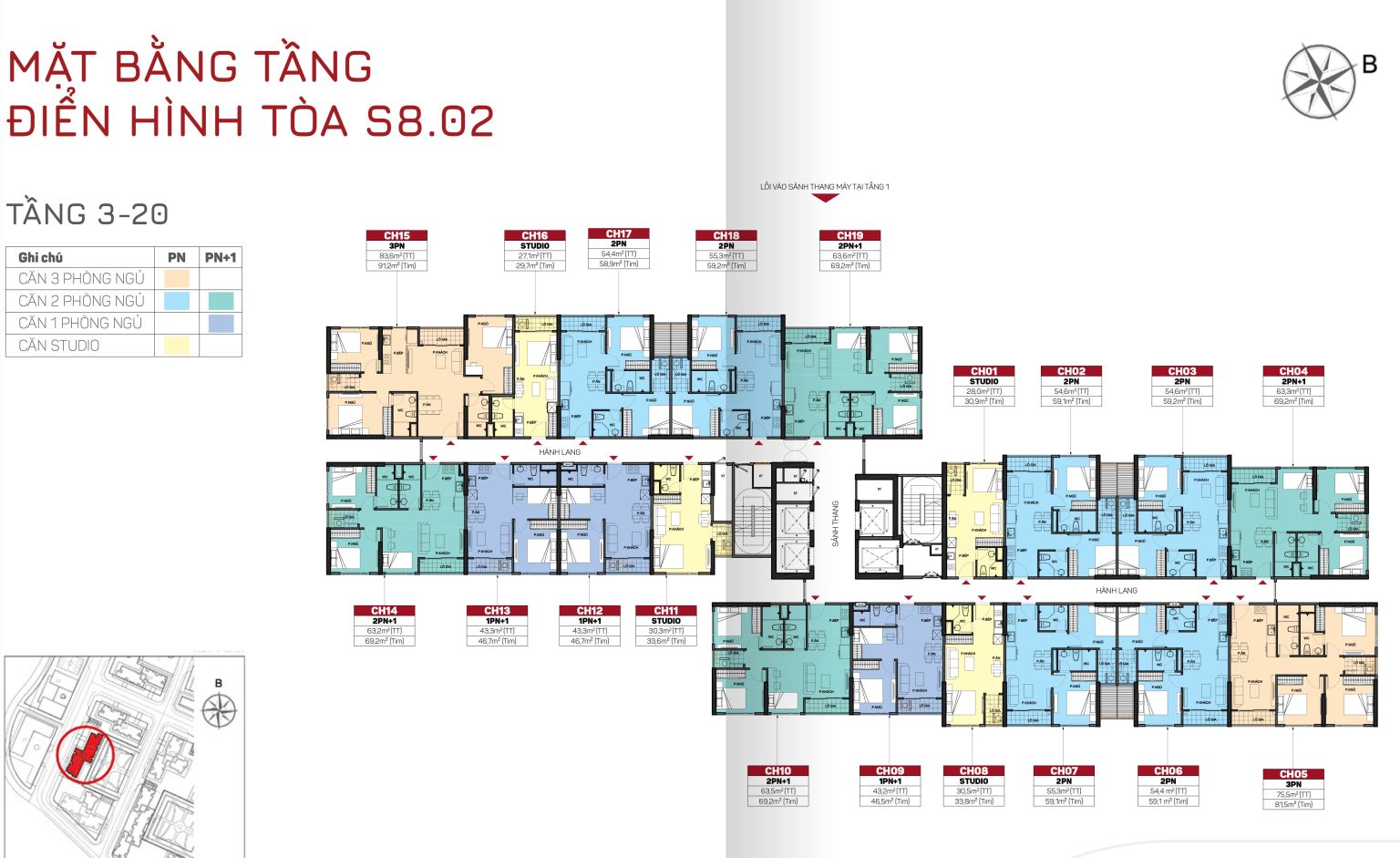
TÒA S8.03
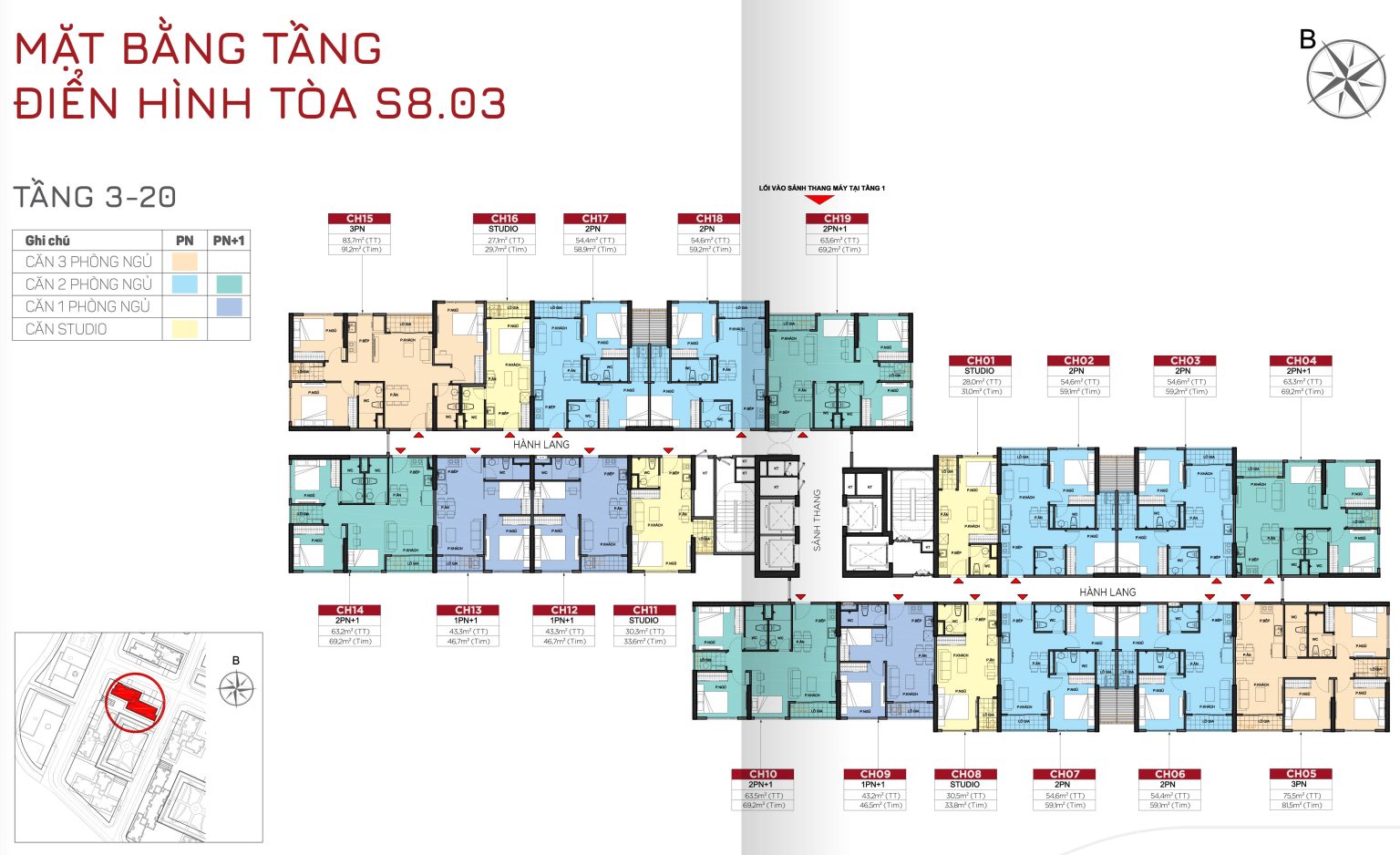
TÒA S9.01
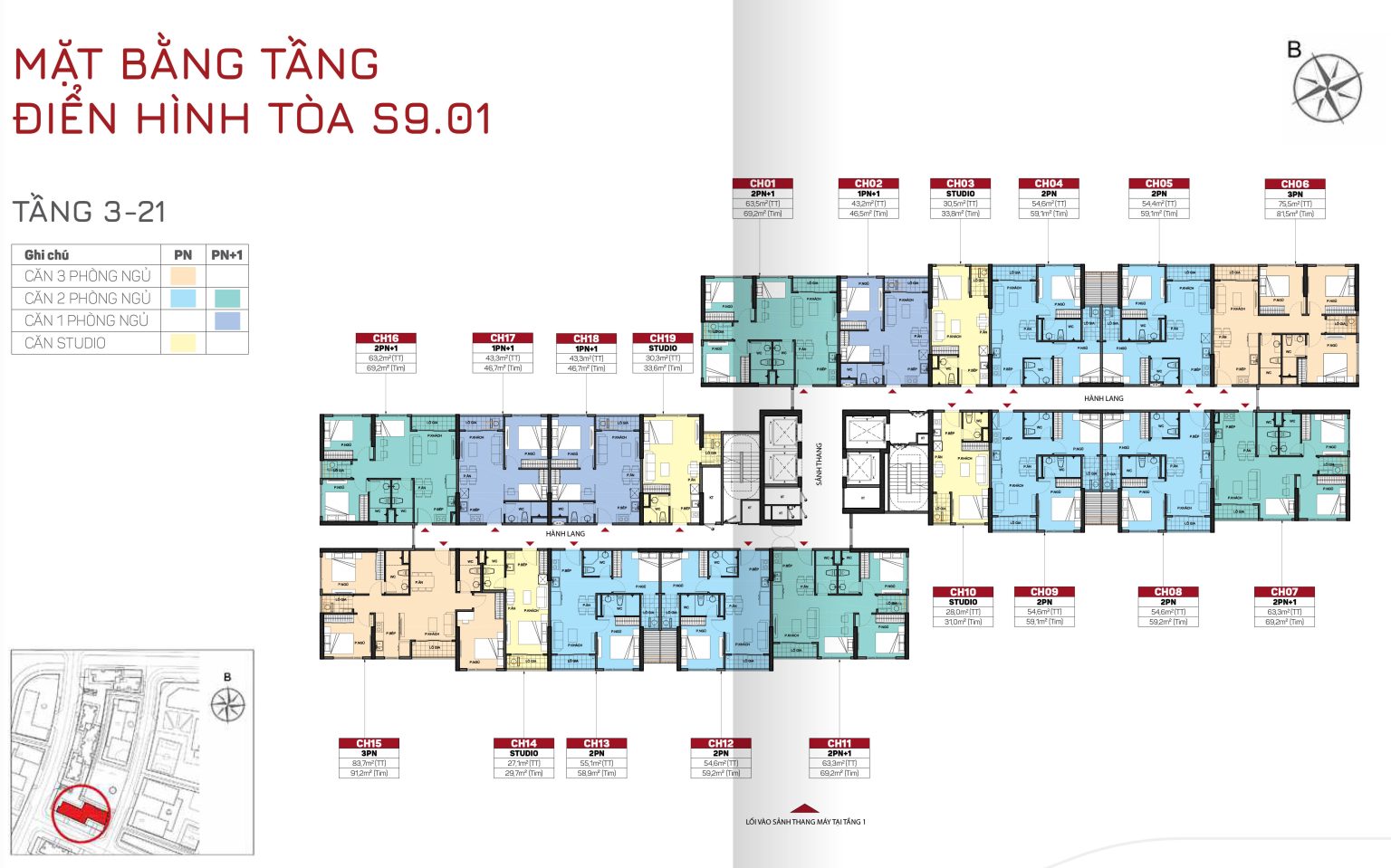
TÒA S9.02
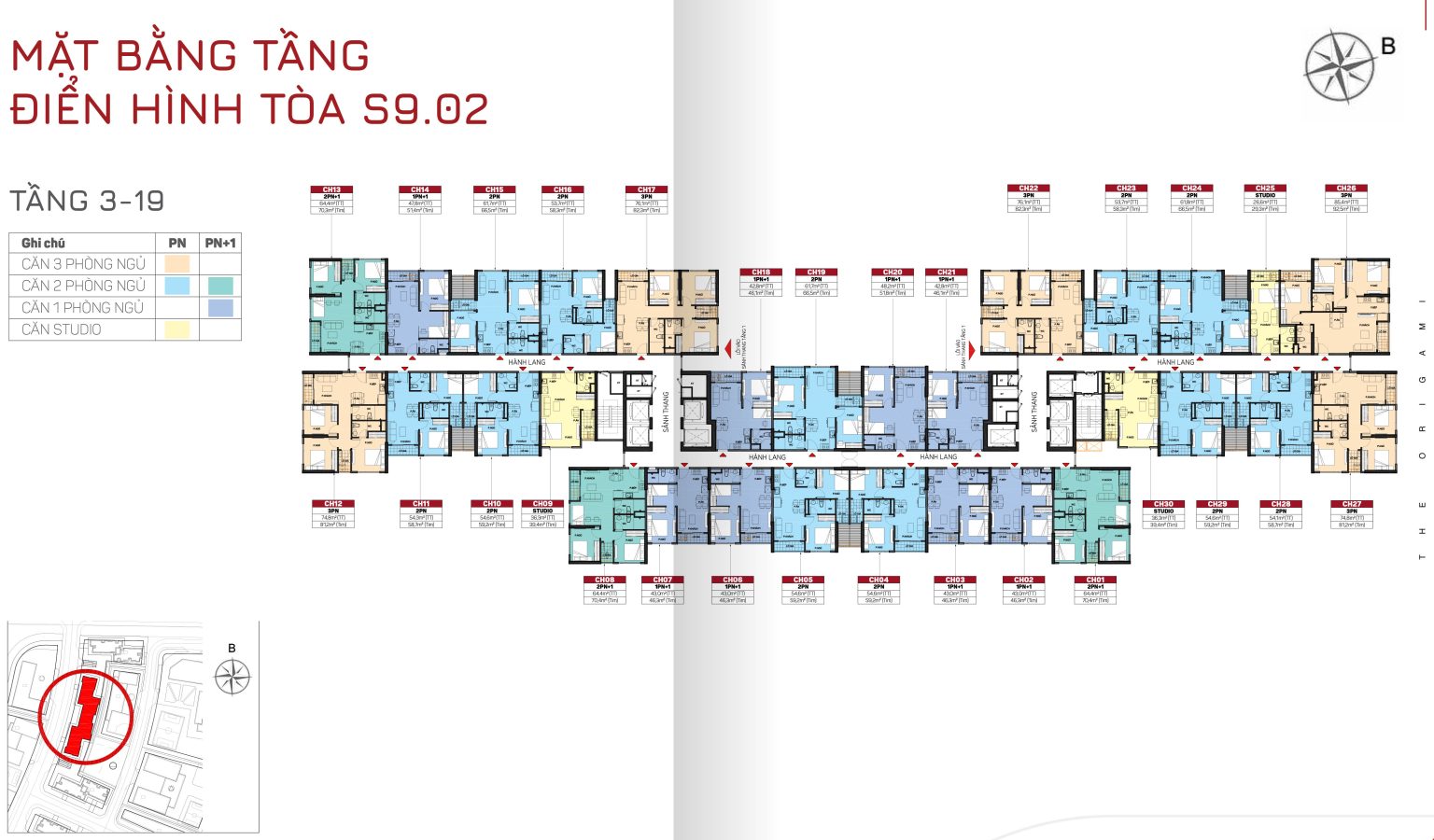
TÒA S9.03
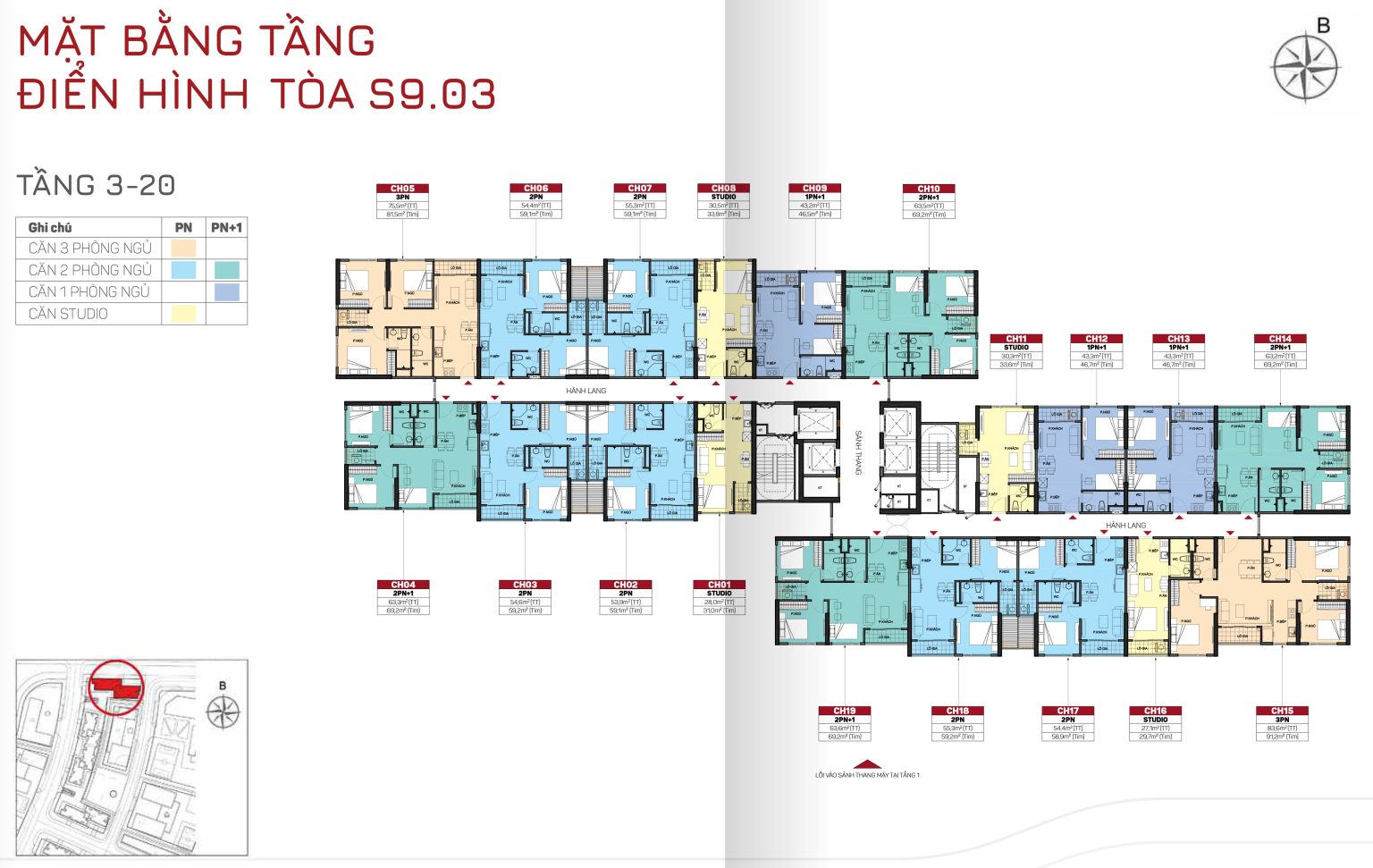
TÒA S10.01
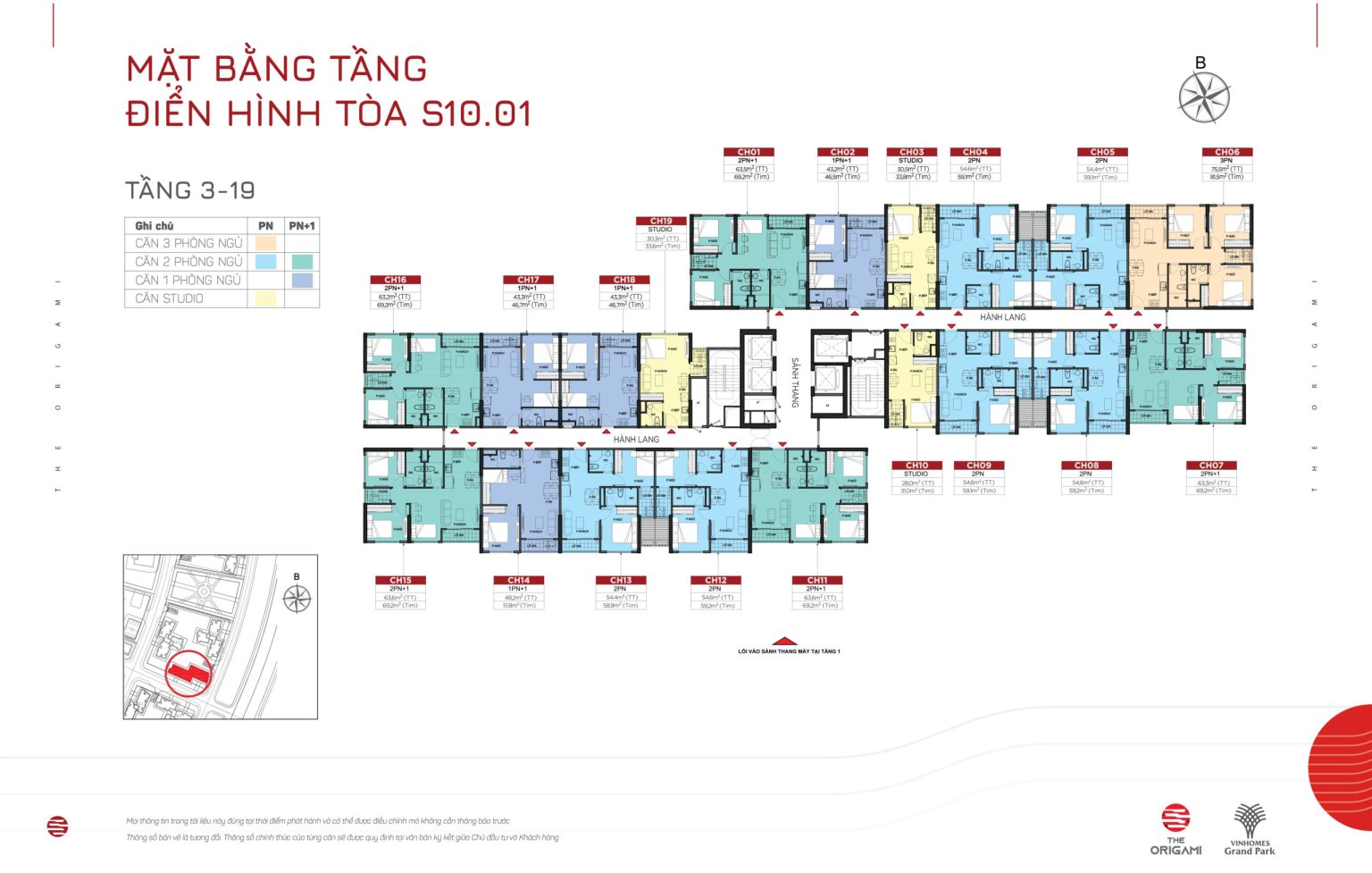
TÒA S10.02
TÒA S10.03
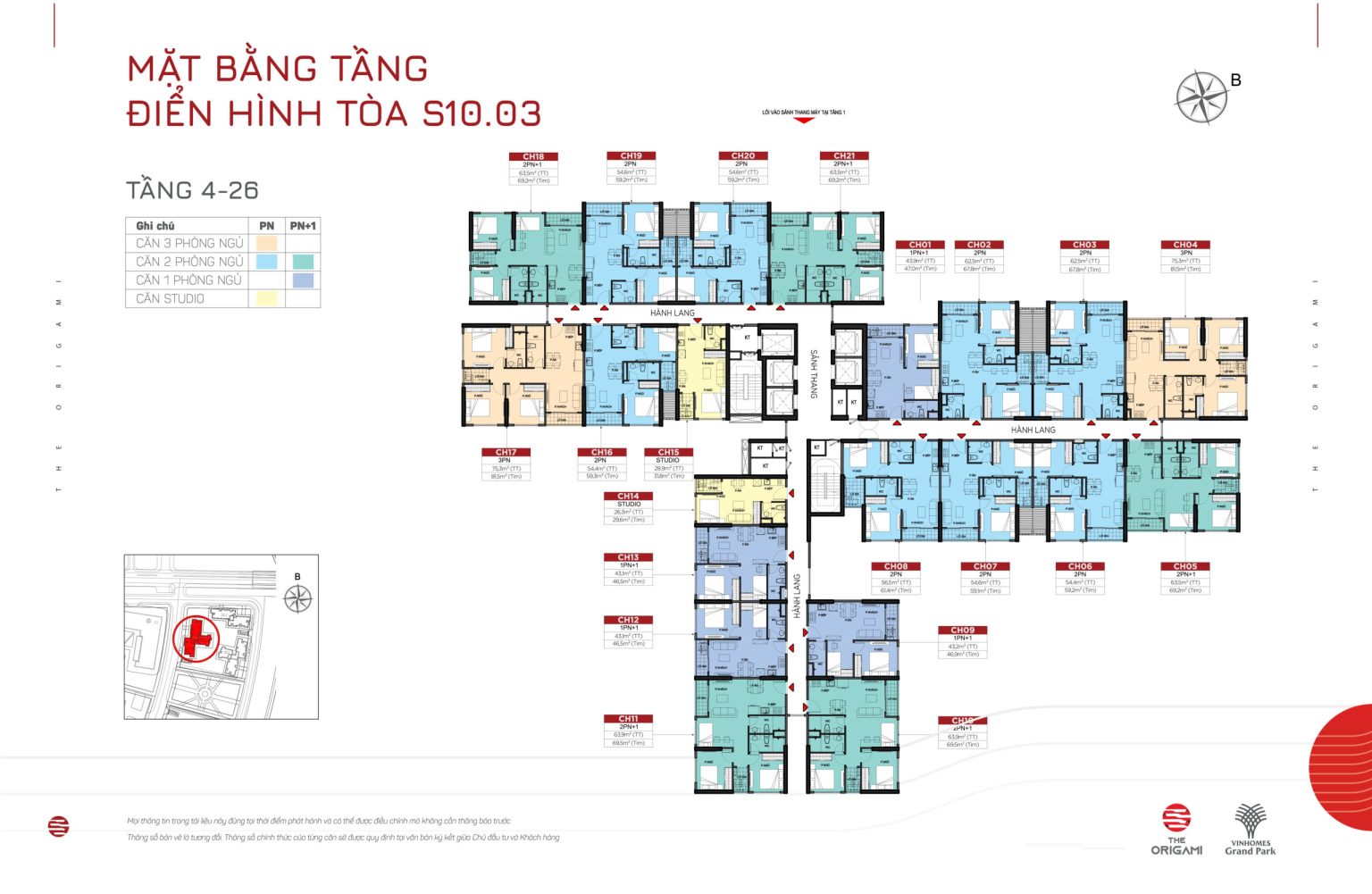
TÒA S10.05
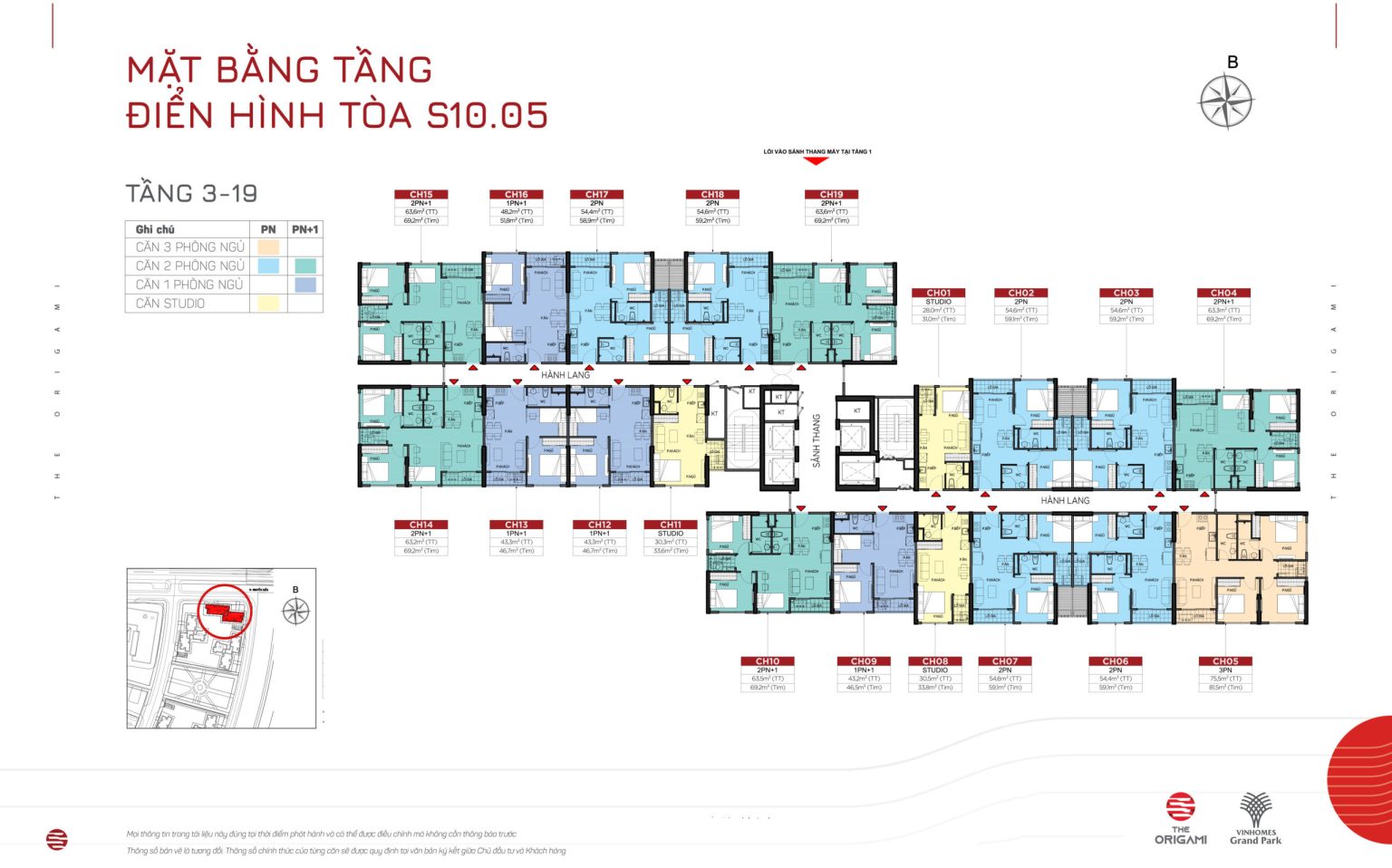
TÒA S10.06
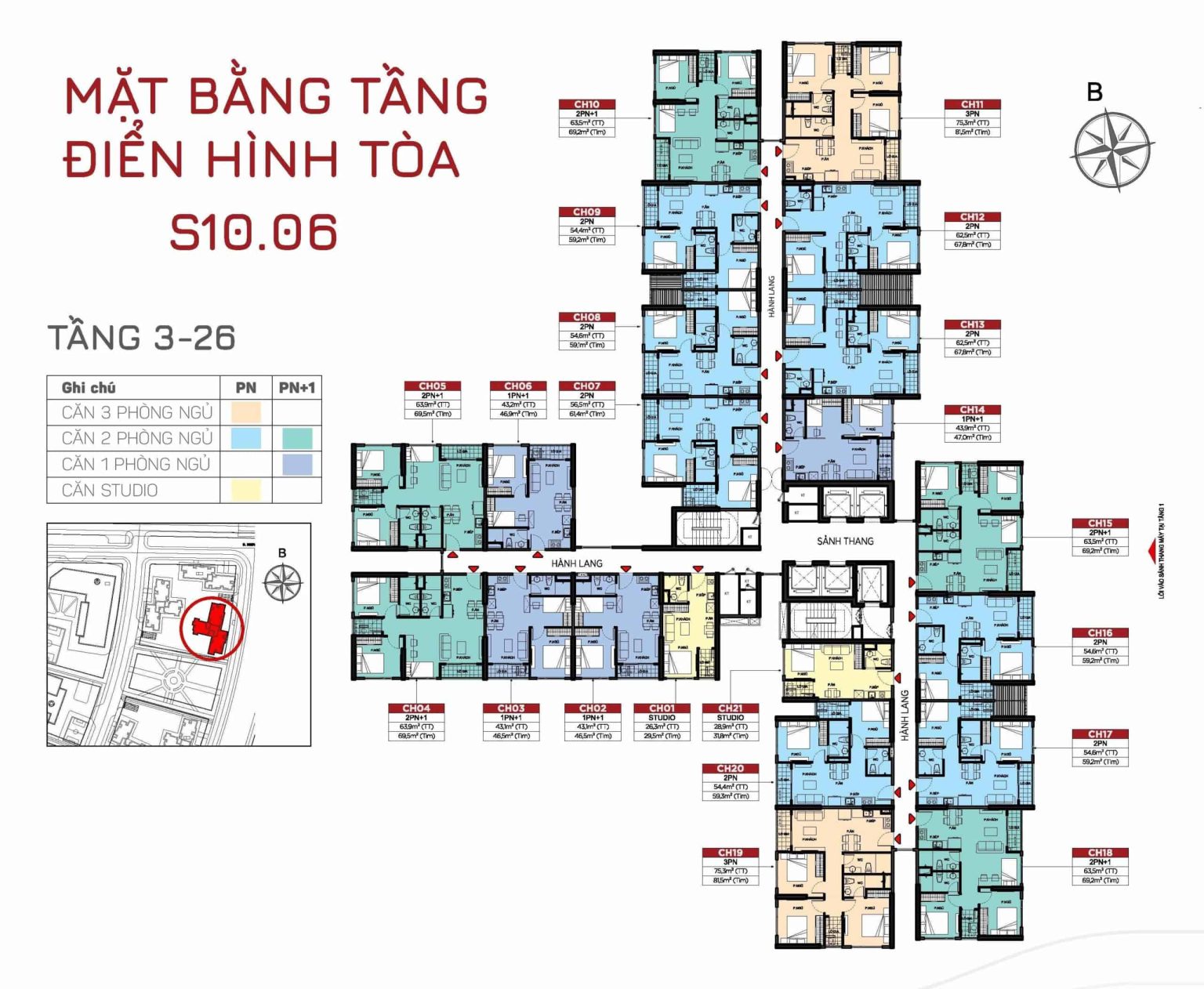
TÒA S10.07
Giá bán và Phương thức thanh toán
The Origami có mức giá vô cùng hấp dẫn, phù hợp với nhu cầu và khả năng tài chính của nhiều nhóm khách hàng dao động từ 1,5 tỷ đến 5,6 tỷ (chưa bao gồm VAT)Tiến độ thanh toán chuẩn
| Đợt | Thời gian | Thanh toán |
| Đặt cọc | Ký TTĐC | 50.000.000 VNĐ |
| Đợt 1 | 7 ngày sau khi ký HĐMB | 15% gồm VAT |
| Đợt 2 | Ngày 20/02/2021 | 15% gồm VAT |
| Đợt 3 | Ngày 20/03/2021 | 15% gồm VAT |
| Đợt 4 | Ngày 20/6/2021 | 5% gồm VAT |
| Đợt 5 | Theo thông báo nhận bàn giao căn hộ | 45% (gồm VAT) + 2% KPBT + VAT của 5% |
| Đợt 6 | Nhận sổ hồng | 5% không gồm VAT |
| TỔNG | 100% | |
Tiến độ thanh toán bằng vốn vay ngân hàng
- Mức dư nợ vay lên đến 80% giá bán (đã bao gồm VAT)
- Hỗ trợ lãi suất 0% trong vòng 24 tháng kể từ ngày giải ngân
- Ân hạn nợ gốc 24 tháng
- Miễn phí trả nợ trước hạn trong thời gian hỗ trợ lãi suất
Phân khu The Beverly - Dự án Vinhomes Grand Park
The Beverly, dự án cao cấp bậc nhất Thành phố Đại công viên Vinhomes Grand Park
The Beverly tiếp tục là phân khu cao tầng thứ 4 được chủ đầu tư Vingroup cung ứng ra thị trường. Đây sẽ là phân khu căn hộ Compound cao cấp nhất tại Đại đô thị Vinhomes Grand Park với quy mô dự kiến khoản 10 toà tháp căn hộ cao 32 tầng.

Phân khu căn hộ The Beverly sở hữu vị trí gần như “hoàn hảo” trong đại đô thị Vinhomes với tầm view trực diện về phía công viên 36ha (công viên ánh sáng lớn nhất Đông Nam Á), xa hơn là khu vực sông Tắc và Sông Đồng Nai, mặt còn lại nhìn về phía công viên nội khu Vinhomes, cụm trường học và khu vực y tế. Ngoài ra, phân khu căn hộ The Beverly còn nằm cạnh Trung tâm thương mại Vincom Mega Mall lớn nhất miền nam. Có thể nói đây là phân khu căn sở hữu vị trí đẹp nhất và thuộc dòng cao cấp nhất tại đại đô thị Vinhomes Grand Park.

Phong cách thiết kế
The Beverly là phân khu ngập tràn không gian nghỉ dưỡng hoà quyện vào thiên nhiên trong lành hiếm có, từ việc thiết kế các toà nhà theo hình chữ Z giúp tối ưu hoá không gian, mang đến không gian sống trang lành và ánh sáng tự nhiên. Hệ sinh thái xung quanh được thiết kế tỉ mỉ với thảm thực vật phong phú, đa dạng, tiểu cảnh đẹp mắt tạo nên khí chất nghỉ dưỡng khác biệt.

The Beverly với quy mô 10 toà tháp căn hộ cao 32 tầng và 2 tầng hầm, được chia thành hai phân khu với tên gọi The Star và The Resort, trong đó:
Phân khu The Star: được ví như “nơi ở của các ngôi sao” với tầm view triệu đô trực diện công viên 36ha và sông Đồng Nai. Công viên nội khu đậm chất hưởng thụ với hơn 30 tiện ích: hồ bơi 3 lớp tầm nhìn công viên 36ha, quầy bar dưới nước theo phong cách Beverly Hills, đường dạo, đại lộ danh vọng, vườn nhiệt đới, khu tập thể dục dưới nước aqua gym…
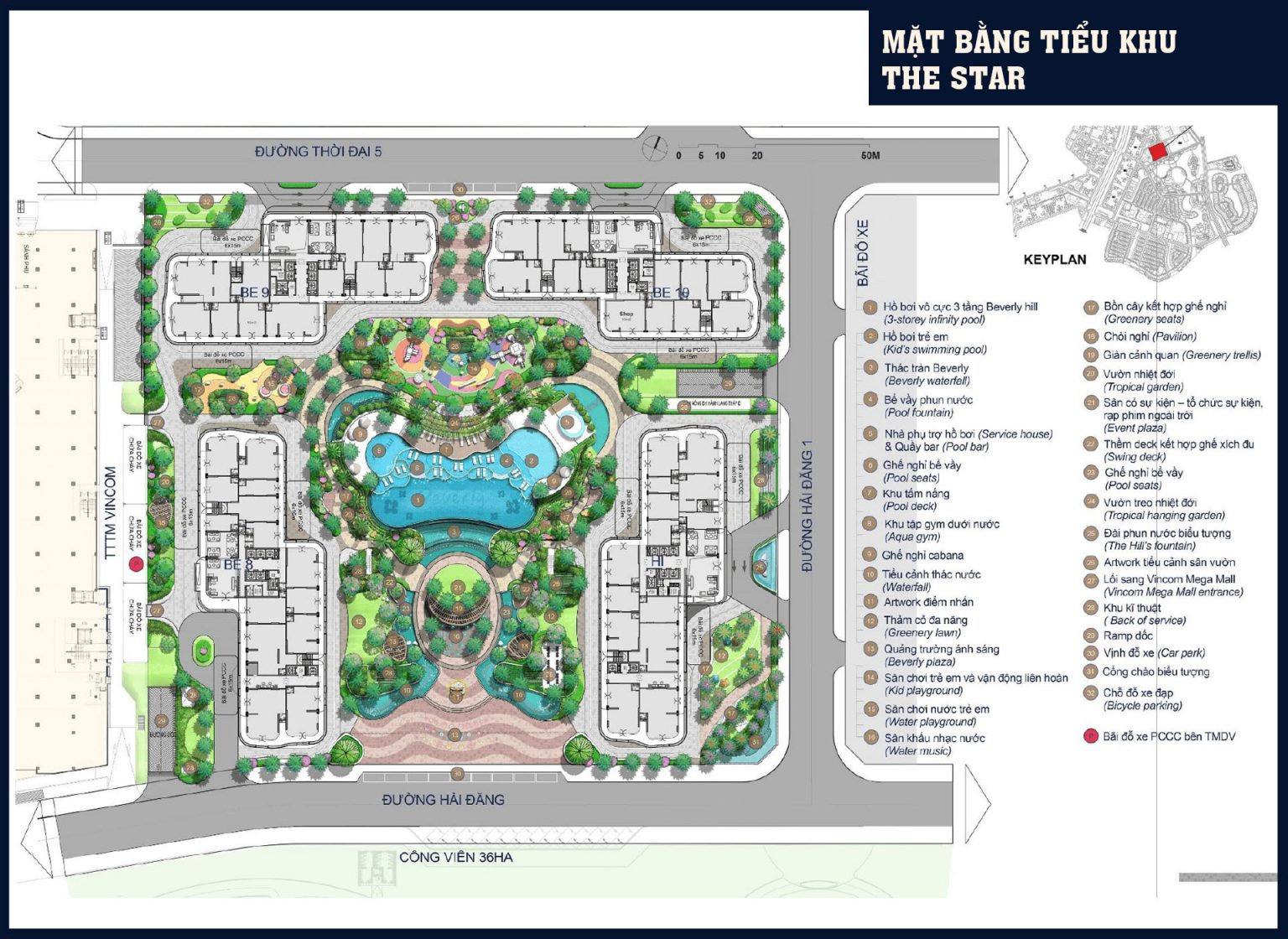
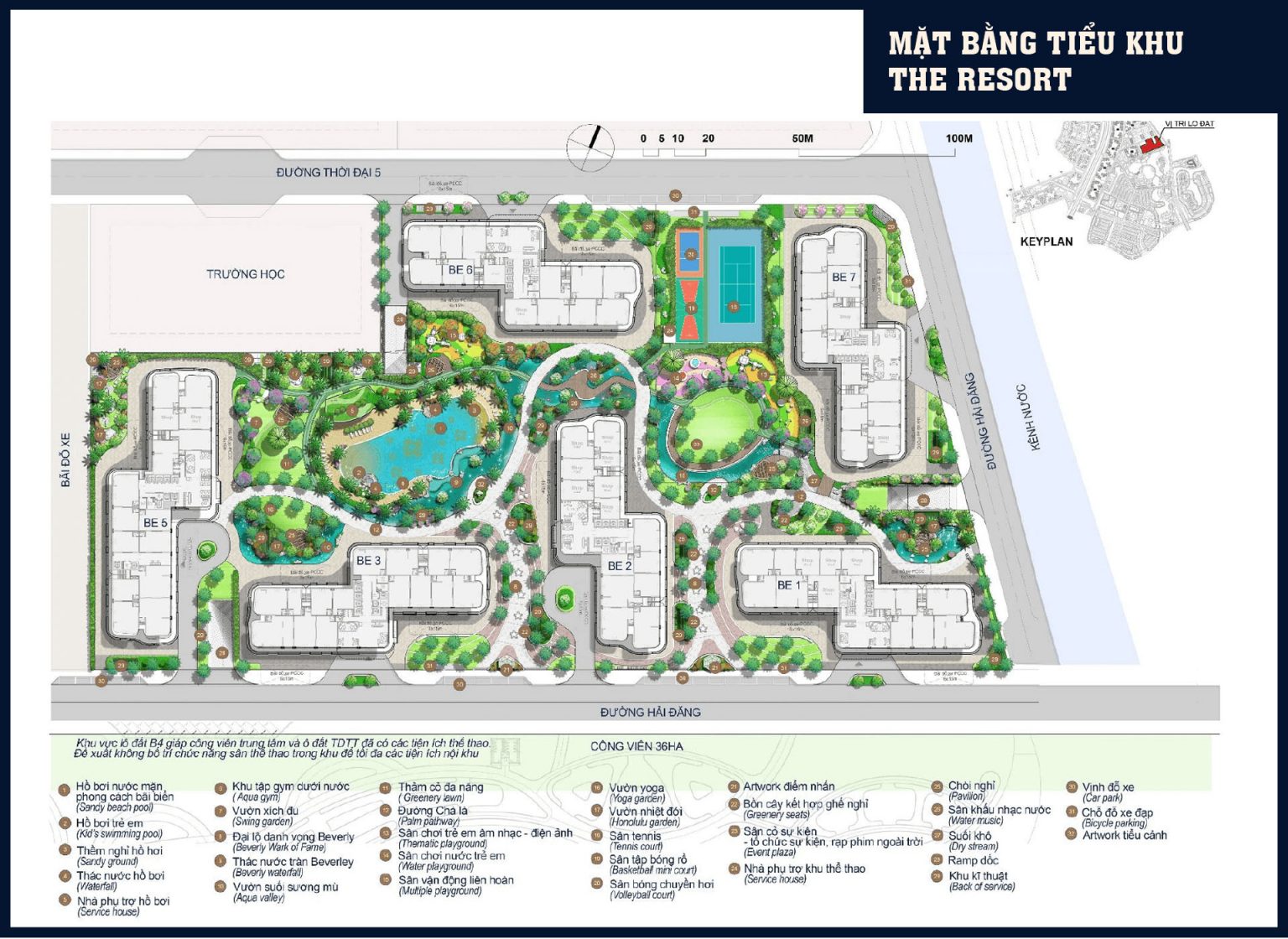
Phân khu Resort: Có diện tích hơn 30.000m2, được Chủ đầu tư dành gần 70% diện tích cho cảnh quan và giao thông với mô hình nghỉ dưỡng đẳng cấp từ các resort nghỉ dưỡng tại Mỹ với điểm nhấn là hồ bơi nước mặn – mang “biển trời” về với cư dân The Beverly; tiện ích trong nhà đẳng cấp, tiêu chuẩn bàn giao cao cấp.
TRẢI NGHIỆM RESORT ĐẬM CHẤT THƯỢNG LƯU




TỔNG QUAN PHÂN KHU THE BEVERLY
|
 |
ĐẶT QUYỀN CƯ DÂN TẠI – THE BEVERLY
1. Toạ lạc tại vị trí trung tâm nhất và sở hữu tầm nhìn bao trọn không gian xanh khoáng đạt của đại công viên trung tâm 36ha – “lá phổi xanh kỳ diệu”.
2. Cảnh quan tiện ích phong cách nghỉ dưỡng sinh thái sang trọng mang lại cho cư dân cuộc sống thư thái đẳng cấp như tại Resort
3. The Beverly dự kiến sẽ có 2 hồ bơi nước mặn đầu tiên và duy nhất tại Đại đô thị Vinhomes Grand Park
4. Ấn tượng với hồ bơi vô cực 3 tầng, dòng thác sương mù và quảng trường ánh sáng nổi bật
5. Ngoài ra, Phân khu Beverly còn sở hữu toà tháp The Hill – biểu tượng thượng lưu, sang trọng cao cấp.

VỊ TRÍ DỰ ÁN THE BEVERLY
Vị trí phân khu căn hộ The Beverly toạ lạc tại nội khu trung tâm Đại đô thị Vinhomes Grand Park, thuộc phường Long Bình và phường Long Thạnh Mỹ, Quận 9, TP.HCM (nay là thành phố Thủ Đức – Thành phố Hồ Chí Minh) đây được xem là vùng phát triển kinh tế trọng điểm phía Đông với hệ thống cơ sở hạ tầng được đầu tư bài bản.


Đại đô thị Vinhomes Grand Park sau khi hoàn thành sẽ trở thành khu đô thị đáng sống bật nhất tại Thành phố Hồ Chí Minh, đây được xem là động lực để thúc đẩy phát triển, thúc đẩy trình độ con người, nâng cao đời sống, tri thức của người dân. Đồng thời giúp chuyển dịch cơ cấu dân số, giải quyết bài toán giãn dân, giảm áp lực lớn đối với hạ tầng giao thông Thành phố hiện nay. Đây là bệ phóng giúp TP.HCM tăng sức cạnh tranh lớn về mọi mặt trên trường quốc tế”.


Tiềm năng thị trường bất động sản quận 9
Là một quận nằm tai khu đông Thành phố Hồ Chí Minh – Quận 9 trở thành tâm điểm của các nhà đầu tư trong nước và quốc tế là do hạ tầng khu vực được đầu tư và phát triển. Thành phố khu Đông nói chung và khu vực Quận 9 nói riêng đang nhận được rất nhiều sự quan tâm từ chính phủ cũng như được kỳ vọng trở thành “điểm sáng” bất động sản mới tại TP.HCM.
Quận 9 với sức hút đặt biệt nhờ vào chính sách quy hoạch hạ tầng giao thông được đẩy mạnh. Với tổng vốn đầu tư lên đến 245.000 tỷ đầu tư vào hạ tầng kết nối tại phía Đông thành phố. Trong đó nổi bật nhất phải kể đến đường song hành cao tốc TP.HCM – Long Thành – Dầu Giây với tổng số tiền được đầu tư lên đến 808 tỷ đồng. Các cung đường lớn như đường Vành Đai 2 (Vành Đai Trong) cũng được mở rộng với 6 làn xe nhằm giảm thiểu ùn tắc giao thông vào giờ cao điểm. Thêm vào đó, tuyến Metro 1, Bến Thành – Suối Tiên sớm đi vào hoạt động sẽ kết nối nhanh chóng quận 9 với các quận trung tâm.
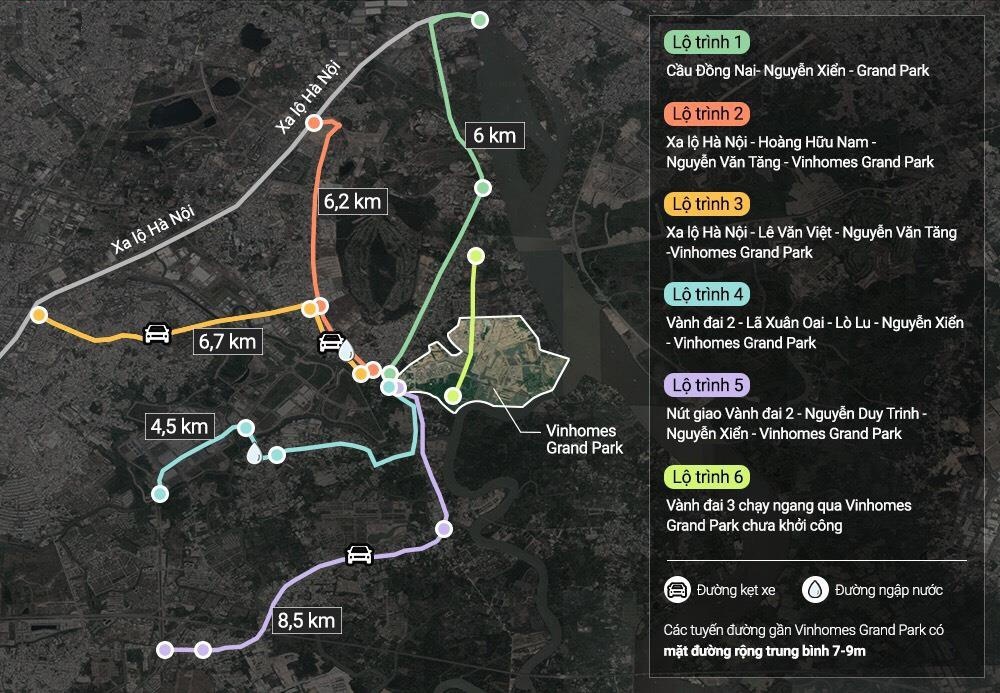
Đặc biệt, khu vực quận 9 còn được hưởng lợi từ việc kết nối thuận tiện qua Xa lộ Hà Nội. Với nhiều ưu thế về hạ tầng giao thông và tiềm lực của khu phía Đông thành phố, các dự án bất động sản cao cấp tại quận 9 sẽ là nơi sinh sống của cộng đồng các chuyên gia, giới tri thức, kỹ sư, bác sĩ, giảng viên đến từ những trường đại học danh tiếng trong khu vực.


Vinhomes Grand Park đại đô thị thông minh đẳng cấp với đầy đủ tiện ích dành cho cư dân như: Mua nhà Vinhomes, mua xe Vinfast, mua sắm đến Vincom, chăm sóc sức khoẻ tại Vinmec và học tại Vinschool… Ngoài ra, tại Vinhomes còn được bố trí đầy đủ các tiện ích nội khu hiện đại như:

- Hệ thống Hồ bơi đạt chuẩn hiện đại.
- Nhà sinh hoạt cộng đồng
- Trường học các cấp với tiêu chuẩn quốc tế
- Phòng khám đạt chuẩn đáp ứng tốt nhu cầu khám chữa bệnh.
- Khu vực tổ chức sự kiện hiện đại, tiện nghi.

- Khu vui chơi trẻ em được bố trí đều tại công viên
- Trung tâm thương mại lớn nhất miền nam .
- Mãng xanh lớn với công viên 36ha
- Cầu dạo bộ, ngắm cảnh tại hồ trung tâm.
- An ninh tuyệt đối với bảo vệ 24/24
“Thành phố công viên – Vinhomes Grand Park” là mô hình đô thị ứng dụng công nghệ và trí tuệ nhân tạo vào quản lý và vận hành nhầm nâng cao chất lượng đời sống cư dân. Chẳng hạn như dùng cảm biến theo dõi tình hình rò rỉ nước sạch, quản lý hệ thống đèn đường, kiểm tra giám sát mức độ ô nhiễm trong không khí, kiểm soát an ninh thông qua nhận diện khuôn mặt,… Giúp nâng cao chất lượng đời sống cư dân được an toàn, thuận tiện, sáng tạo và văn minh.
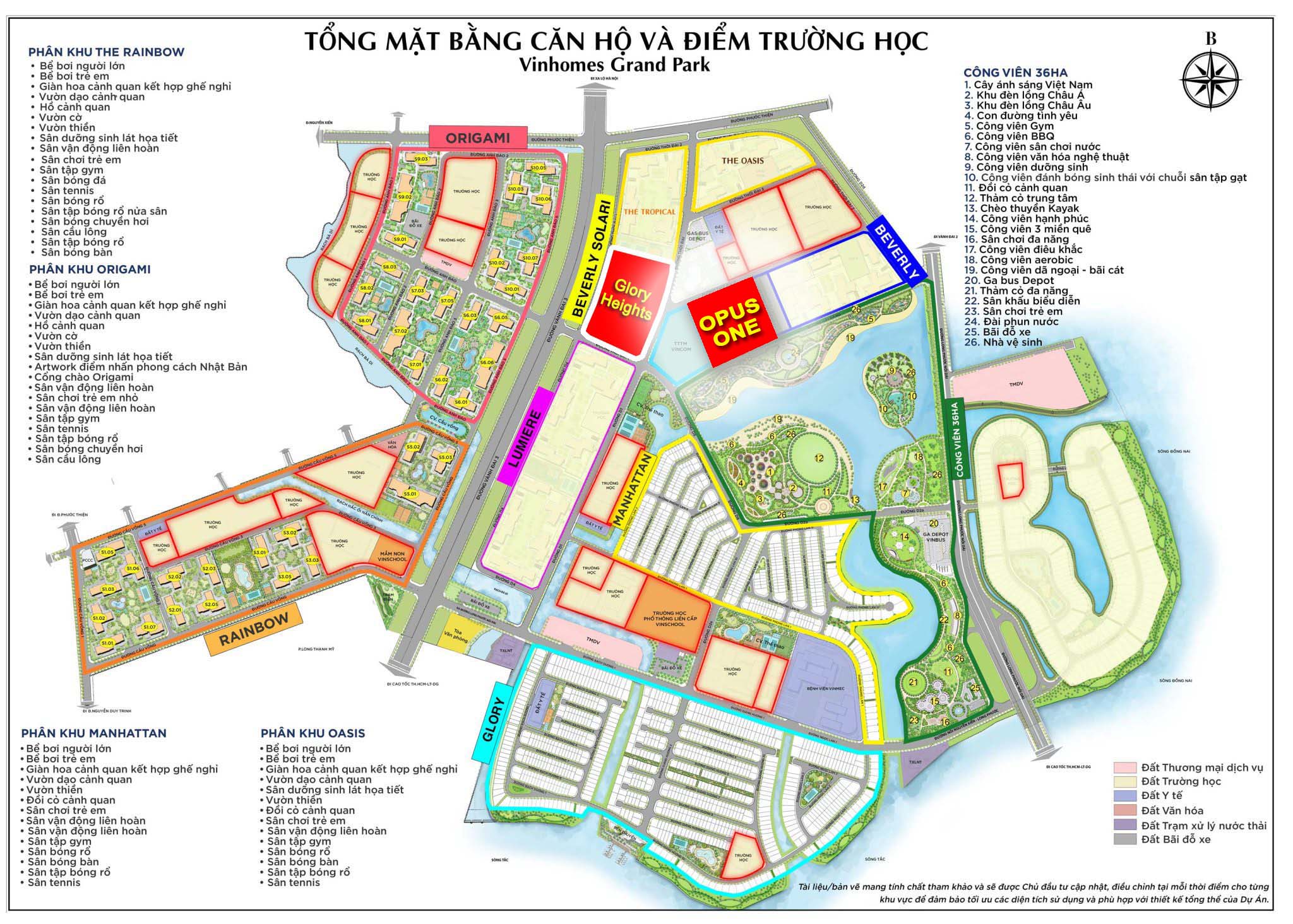
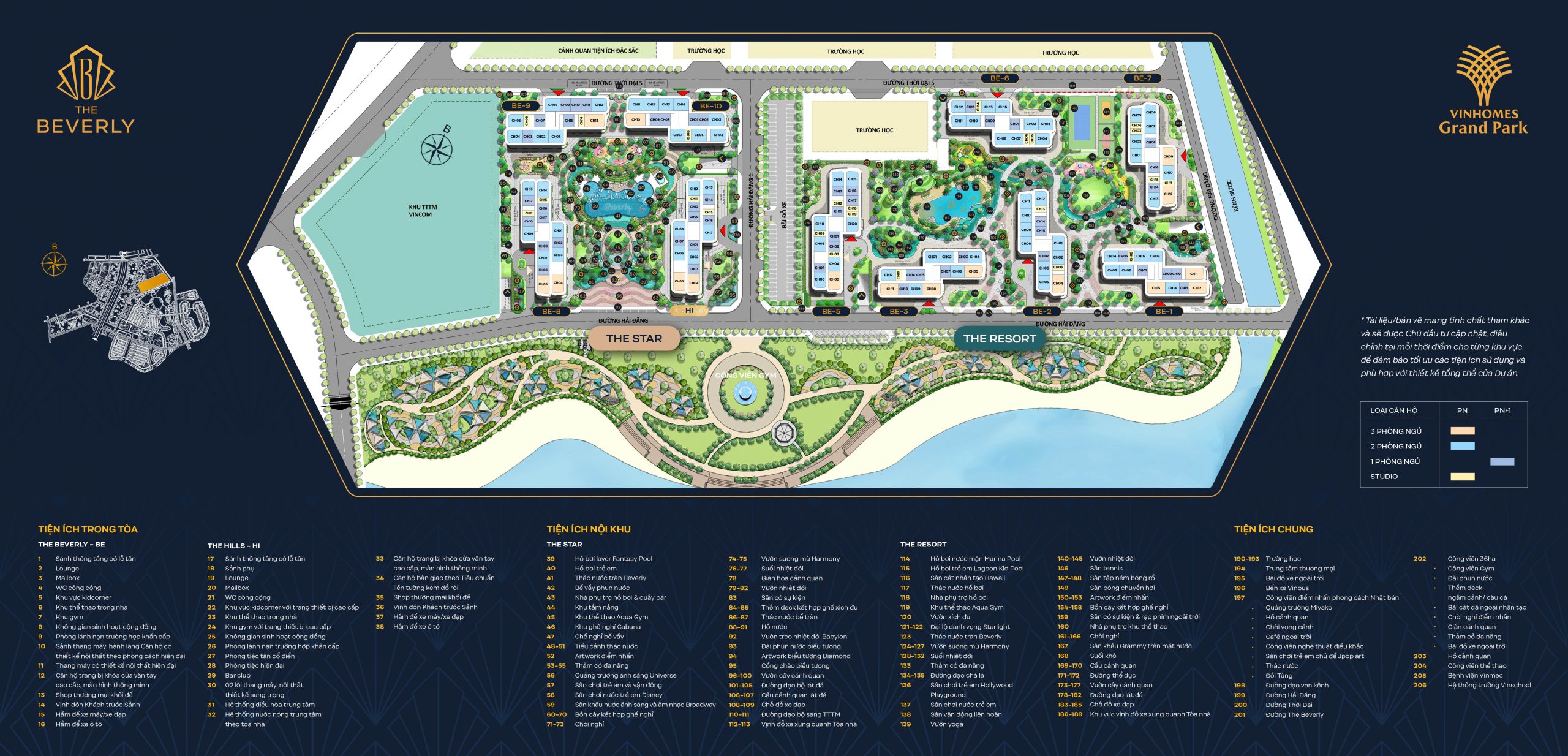
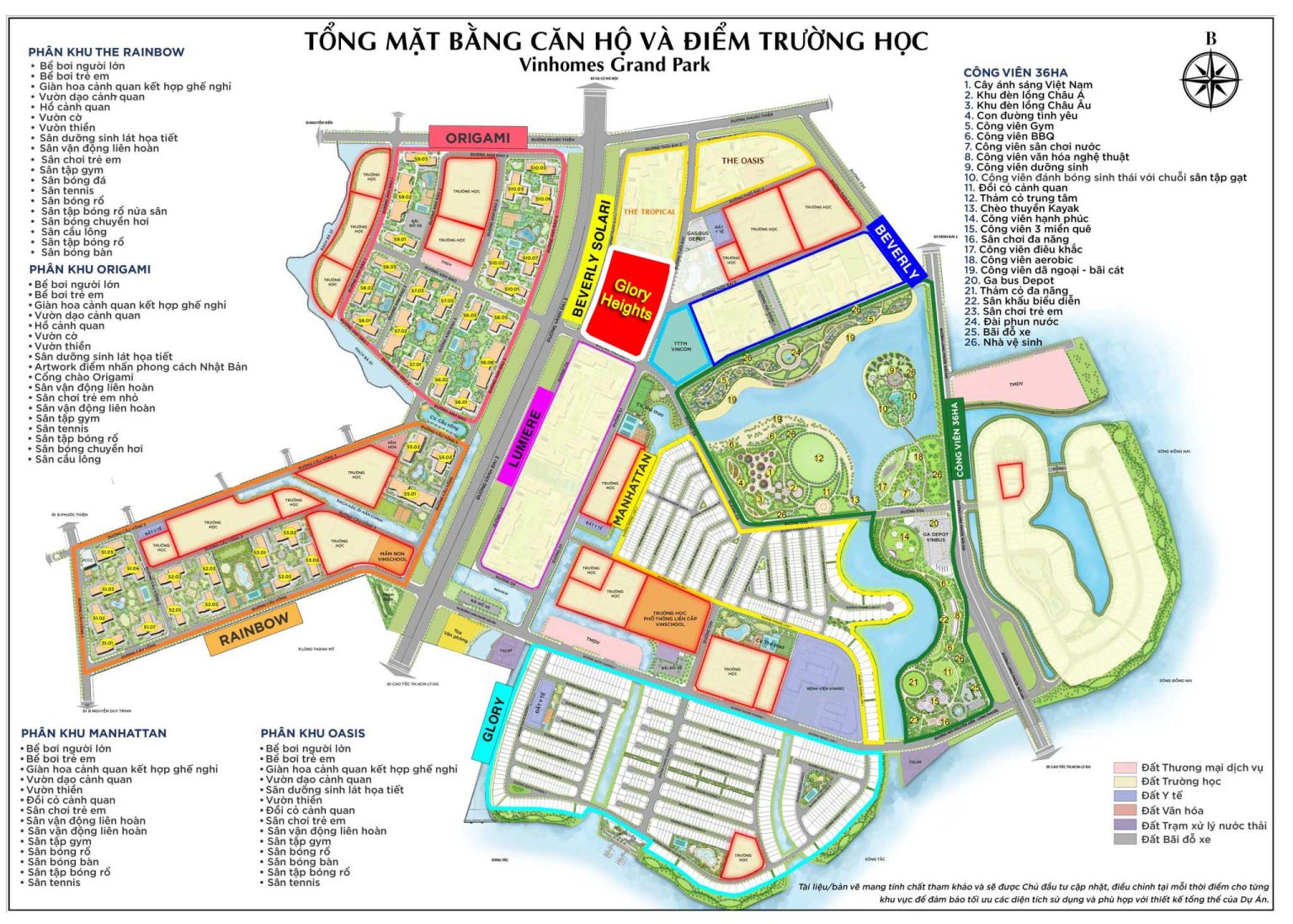
MẶT BẰNG TỔNG THỂ KHU ĐÔ THỊ VINHOMES GRAND PARK
“Thành phố công viên” Vinhomes Grand Park có tổng diện tích 271Ha, nằm tại hai tuyến đường Nguyễn Xiển và đường Phước Thiện, thuộc phường Long Bình và phường Long Thạnh Mỹ quận 9, thành phố Hồ Chí Minh. Là khu đô thị hiện đại bật nhất tại phía đông thành phố với chuỗi tiện ích compound đẳng cấp và có đa dạng các dòng sản từ căn hộ, nhà phố, shophouse, boutique, duplex, penhouse và dinh thự cao cấp.
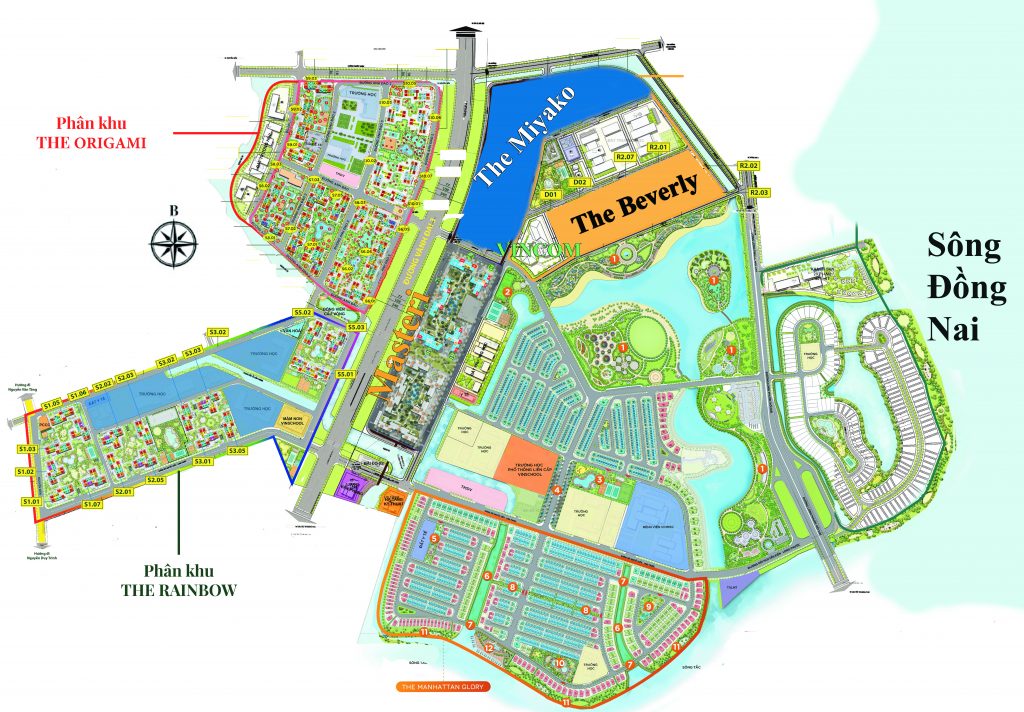
Vinhomes Grand Park với tổng số lượng sản phẩm 44.000 căn hộ cao cấp và hơn 1.600 sản phẩn nhà phố thấp tầng, được chia thành nhiều phân khu với tên gọi lần lượt là:
Phân khu 1 – The Rainbow (đã bán hết)
Phân khu 2 – The Origami (đang triển khai)
Phân khu 3 – The Miyako (sắp triển khai)
Phân khu 4 – The Beverly (đang triển khai)
MẶT BẰNG PHÂN KHU CĂN HỘ THE BEVERLY
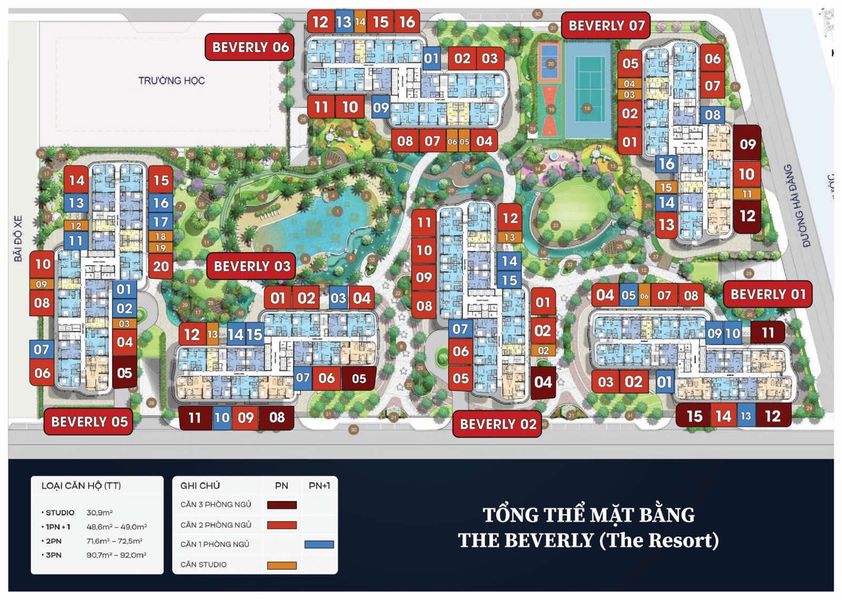
Phân khu căn hộ The Beverly có diện tích khoảng 10ha được quy hoạch thành hai cụm tiểu khu nhỏ với tên gọi The Star và The Resort, được ngăn cách nhau bởi các trục đường nội khu và các công trình công cộng.
Tiểu khu 1 The Star: Có 4 tòa tháp căn hộ bao gồm các tòa hình chữ “Z”. Điểm nổi bật là nằm cạnh Trung tâm thương mại Vincom Mega Mall lớn nhất miển Nam.
Tiểu khu 2 The Resort: Có 6 tòa tháp, bao gồm các tòa tháp có hình chữ “Z”. Điểm nổi bật là tiện ích nội khu chuẩn resort và cạnh sông Đồng Nai thơ mộng.
Mặt bằng các căn hộ, các tòa tại đây cũng được đánh giá cao về cách thiết kế cũng như tiện ích.
Các tòa thường có khoảng 6 – 8 thang máy, được thiết kế để lấy gió tự nhiên mà không cần đến điều hòa.
Hành lang các căn hộ rộng đến 1,6m, thiết kế đẳng cấp chuẩn khách sạn 5 sao và cũng được thiết kế thông gió tự nhiên, không cần điều hòa.

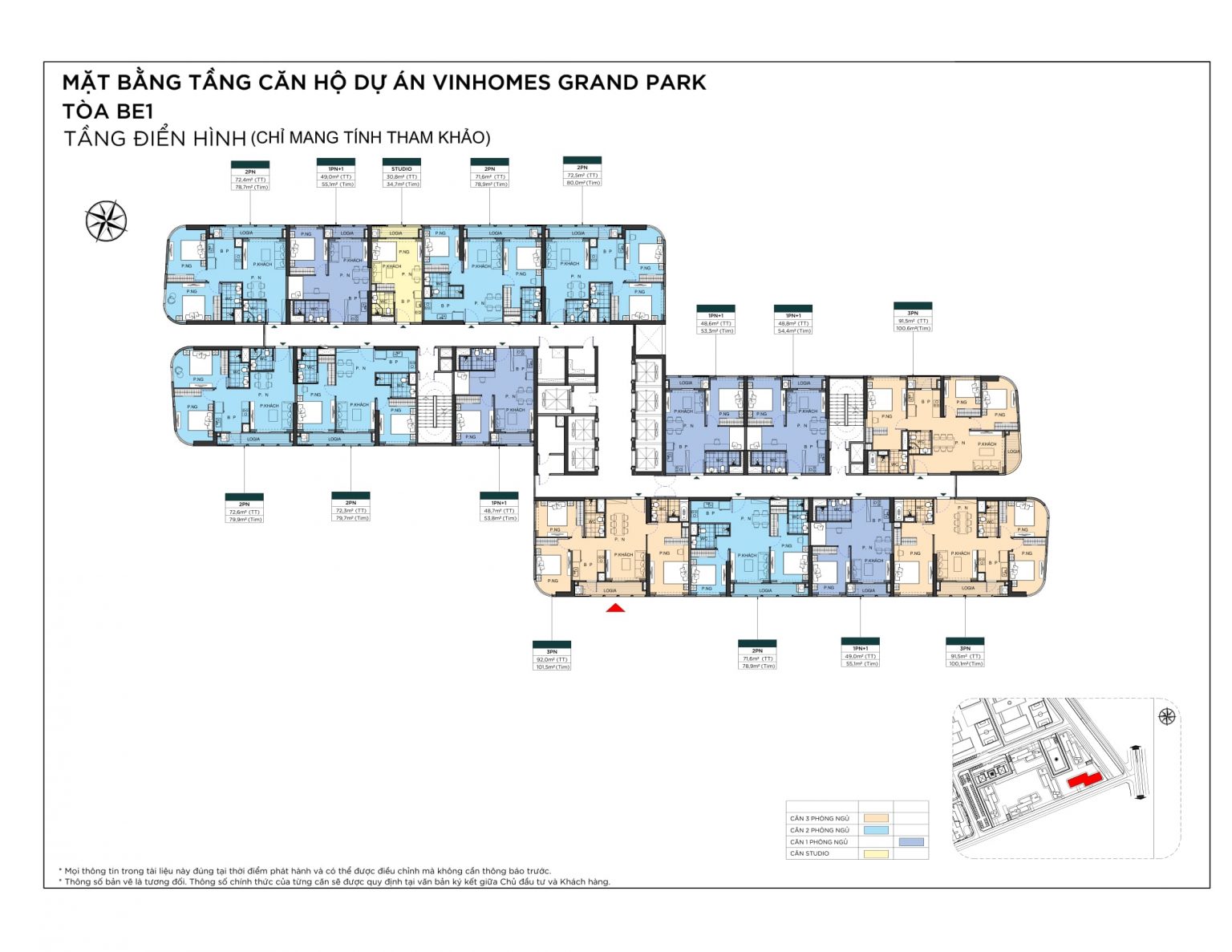
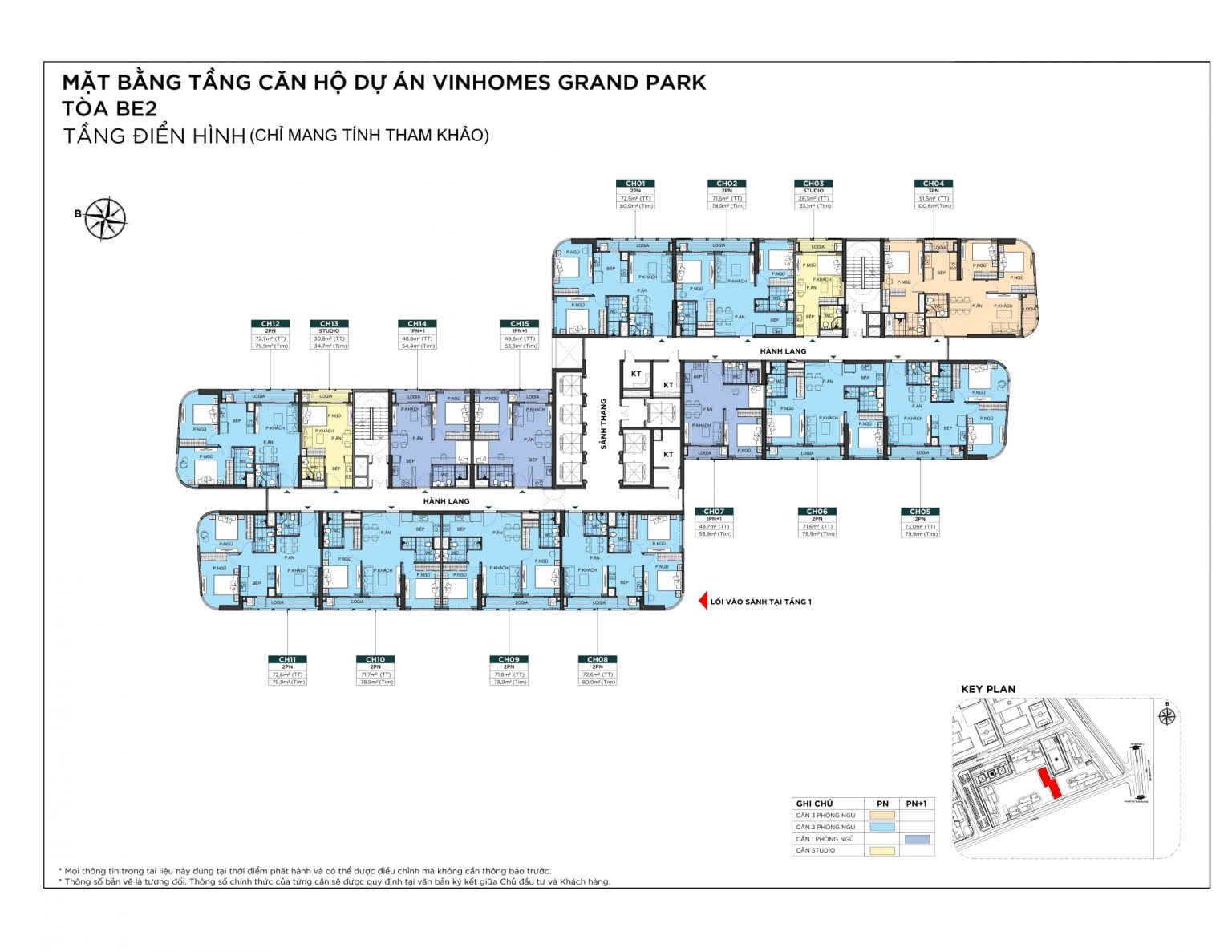
Mặt bằng toà tháp Empire - The Beverly
Mặt bằng căn hộ – The Beverly
Chiều cao tầng căn hộ là 3,2m, thông thủy 2,7m.
Chiều cao tầng shophouse là 4,4m, thông thủy 3m.
Chiều cao tầng hầm là 3,3m, thông thủy là 2,7m.
Trục kỹ thuật của tòa nhà 1 phần âm tường, 1 phần bên ngoài tòa nhà và cơ chế thoát mùi ngang.
Diện tích mặt bằng lớn nhưng mật độ xây dựng của The Beverly lại thấp nhất trong số 4 phân khu. Cùng với đó là mảng xanh được ưu tiên tối đa, hứa hẹn là phân khu đẳng cấp bật nhất tại Đại đô thị Vinhomes Grand Park.
PHỐI CẢNH CĂN HỘ THE BEVERLY
Các căn hộ thuộc phân khu The Beverly được thiết kế từ 1 – 3 phòng ngủ, được bàn giao theo tiêu chuẩn cao cấp gồm hệ thống đèn chiếu sáng, sàn gỗ tại tất cả các phòng, vách kính tắm đứng bên trong căn hộ và điểm nổi bật là tất cả các căn hộ tại The Beverly đều có hai view với diện tích giao động từ 32 – 105m2. Dự kiến, những căn hộ đầu tiên sẽ được hoàn thiện và bàn giao vào năm 2023.
- Căn Studio có diện tích từ: 32 – 33m2
- Căn 1 phòng ngủ (+) có diện tích từ: 53 – 55m2
- Căn 2 phòng ngủ có diện tích từ: 78 – 80m2
- Căn 3 phòng ngủ có diện tích từ: 100 – 105m2










CHÍNH SÁCH DÀNH CHO KHÁCH HÀNG
Một trong những nỗi trở ngại và băn khoăn lớn nhất của người mua nhà luôn là vấn đề về tài chính, đặc biệt giữa thời điểm dịch Covid-19 khiến thu nhập của nhiều người bị ảnh hưởng. Trong bối cảnh này, Vinhomes phối hợp cùng ngân hàng Techcombak, Vietcombank và MBBank đưa ra các chương trình ưu đãi vô cùng hấp dẫn, đem đến cơ hội sở hữu căn hộ tại Vinhomes với vốn tự có chỉ 15% trên tổng giá trị căn hộ và được kèm theo chính sách ân hạn nợ gốc và lãi xuất 0% đến khi nhận nhà. Có thể nói đây là chính sách tốt nhất trên thị trường bất động sản hiện nay.
Hỗ trợ vay từ 80 – 100% giá trị sản phẩm
- Hỗ trợ ân hạn gốc lên đến 3 năm
- Hỗ trợ lãi xuất 2 năm đầu cố định từ 7 – 7,5%/năm
- Tặng Voucher Vinfast từ 70 – 200 triệu
Các căn hộ thuộc phân khu The Beverly sẽ được bàn giao theo tiêu chuẩn Ruby cao cấp bật nhất từ trước đến nay. Ngoài ra để linh hoạt trong việc thay đổi hoặc nâng cấp nội thất tại phòng bếp của căn hộ, chủ đầu tư dự kiến sẽ không bàn giao tủ bếp. Tuy nhiên, khách hàng sẽ được tặng gói thiết kế nội thất tương ứng với từng loại căn hộ. Đặt biệt, khách hàng không nhận gói nội thất có có thể trừ trực tiếp vào giá bán.

Phân khu Glory Heights - Dự án Vinhomes Grand Park
Glory Heights là phân khu trung tâm, đẹp nhất của dự án Vinhomes Grand Park. Phân khu Glory Heights chính là mảnh ghép hoàn hảo cuối cùng hoàn thiện tầm vóc của một khu đô thị hiện đại và sầm uất bậc nhất của Thành phố mới Thủ Đức.

Phân Khu Glory Heights Vị trí tiềm năng ngay đối diện TTTM Vincom Mega Mall lớn nhất TP.HCM. Sở hữu phong cách thiết kế ấn tượng cùng hệ thống tiện ích đậm chất resort nghỉ dưỡng kiểu Mỹ, kiến tạo cuộc sống hiện đại, đẳng cấp và tiện nghi cho cư dân. Hưởng trọn lợi thế tiềm năng tăng giá trong tương lai với hạ tầng được kết nối đồng bộ: đường Vành đai 3 đi ngang dự án, gần cao tốc TP. HCM – Long Thành kết nối thuận tiện đến sân bay Long Thành và các tỉnh thành lân cận.
Glory Heights với ý nghĩa “ánh hoàng hôn” tên gọi này được lấy cảm hứng từ tầm nhìn đón hoàng hôn buổi chiều tà tuyệt đẹp tại tiểu khu Glory Heights, nơi cư dân cảm nhận được sự lãng mạn của ánh nắng hoàng hôn động lại trước thềm nhà vào cuối ngày.
|
PHÂN KHU TRUNG TÂM ĐẮC ĐỊA NHẤT ĐÔ THỊ VINHOMES GRAND PARK
⭐️ 07 NĂM KHÔNG LO LÃI SUẤT ⭐️ ⭐️ BẢN SAO CỦA LANDMARK 81 ⭐️ ⭐️ NGAY TTTM VINCOM LỚN NHẤT ⭐️
Không chỉ có mức giá dự kiến cực tốt với vị trí ngay tâm điểm thương mại Vinhomes Grand Park, căn hộ Glory Heights còn sở hữu chính sách bán hàng “Xứng tầm GUINNESS” với 03 CHÍNH SÁCH LINH HOẠT VÀ CHÍNH SÁCH “BOM TẤN”: ⭐️BOOKING ƯU ĐÃI NGAY 10%⭐️ |
TỔNG QUAN DỰ ÁN
| ✅ Tên dự án | Glory Heights |
| ✅ Chủ đầu tư | Tập đoàn Vinhomes hợp tác cùng Mitsubishi (Nhật Bản) |
| ✅ Vị trí | Trung tâm đại đô thị Vinhomes Grand Park, TP.Thủ Đức |
| ✅ Đơn vị xây dựng | Coteccons, Hòa Bình, Central |
| ✅ Đơn vị quản lý vận hành | Vinhomes |
| ✅ Quy mô | 5 Block, cao từ 26 – 32 tầng |
| ✅ Mật độ xây dựng | 25% |
| ✅ Tổng số lượng sản phẩm | 2.000 căn |
| ✅ Loại hình sản phân | Căn hộ cao cấp, Shophouse |
| ✅ Chức năng khối đế | Shophouse, sảnh lễ tân |
| ✅ Diện tích căn hộ | Studio: 27m2 – 39,4m2 1PN+1: 46,1m2 – 51,8m2 2PN: 58,3m2 – 69,2m2 2PN+1: 69,2m2 – 70,4m2 3PN: 81,2m2 – 103,3m2 |
Phân khu Glory Heights sở hữu vị trí hoàn hảo tại trung tâm đại đô thị Vinhomes Grand Park, nơi đây cực kỳ thuận lợi cho việc di chuyển và đáp ứng đầy đủ nhu cầu vui chơi, giải trí, ăn uống và nghỉ dưỡng dành cho cư dân. Glory Heights nằm trong khu đô thị mới giúp cung cấp một môi trường sống trong lành và yên tĩnh nhưng không kém phần hiện đại.
Cùng với đó, Glory Heights còn sở hữu tiềm năng lớn khi nằm cạnh trung tâm thương mại Vincom Mega Mall lớn nhất miền Nam, nằm cạnh công viên ánh sáng 36ha, cạnh đại lộ mua sắm The Manhattan và cạnh quảng trường Golden Eagle với thiết kế độc đáo.
Ngoài ra dự án còn nằm rất gần với các tiện ích tại khu đô thị như Tòa tháp văn phòng hạng A Vinhomes, gần với hệ thống trường học mầm non và trường liên cấp Vinschool.
Song song đó, liên kết vùng tại dự án Glory Heights cũng không kém phần nổi bật với nhiều tiện ích ngoại khu và còn rất thuận tiện duy chuyển các khu vực lân cận như: Khu công nghệ cao, khu làng đại học Thành phố, bến xe miền đông, trạm metro số 1 và cũng rất thuận tiện duy chuyển về trung tâm thành phố qua tuyến Xa lộ Hà Nội, đường Vành Đai 3, Đường Nguyễn Xiển, Phước Thiện…

Phố biển Malibu
Lấy cảm hứng từ biển Malibu (Mỹ), hồ bơi nội khu Vinhomes Glory Heights mang đậm chất nghỉ dưỡng nhiệt đới cao cấp với chuỗi hồ bơi Malibu có diện tích hơn 845m2 gồm: hồ bơi người lớn, hồ bơi trẻ em và hồ thác tràn vô cực.

Công viên khủng long
Ngoài ra Phố biển Malibu, Glory Heights còn có Công viên khủng long lần đầu tiên xuất hiện tại Vinhomes Quận 9: dự án còn cung cấp hàng loạt tiện ích cao cấp như sân chơi trẻ em chủ đề Khủng long, Chòi nghỉ trứng khủng long, Sân gym ngoài trời, sân yoga, Suối bậc cảnh quan, Vườn cát thám hiểm, Vườn cọ nhiệt đới San Mariano, Đường dạo mạch vòng dài hơn 400 mét, Ghế nghỉ Sunkenmang đến trải nghiệm cuộc sống độc đáo, riêng tư cho cư dân.

Cùng với đó, tại tiểu khu Glory Heights còn sở hữu vị trí đắc địa khi nằm cạnh trung tâm thương mại Vincom Mega Mall lớn nhất miền Nam. Nơi đây được xem là vị trí kim cương sầm uất nhất tại đại đô thị Vinhomes Grand Park. Hứa hẹn là sự kết hợp giữa tiện nghi, cao cấp, thuận lợi là sự lựa chọn hoàn hảo cho những ai muốn một cuộc sống năng động và hiện đại.

Mặt bằng phân khu Glory Heights được xây dựng với 5 tòa tháp cao từ 26 đến 32 tầng, có 2 tầng hầm và khu vực shophouse tại khối đế. Các tòa tháp căn hộ tại Glory Heights được thiết xây dựng với các tòa hình chữ Z, U, T giúp các căn hộ có được tầm view thoáng đãng và đón gió tự nhiên.

Trong phân khu Glory Heights, có rất nhiều căn hộ cao cấp với thiết kế độc đáo và tối ưu, cung cấp cho người dân một không gian sống thoải mái và sang trọng. Tổng thể phân khu Glory Heights tại Vinhomes là một lựa chọn hoàn hảo cho những người muốn sống trong môi trường yên tĩnh và tiện nghi, với những tiện ích đầy đủ và gần gũi với thiên nhiên.
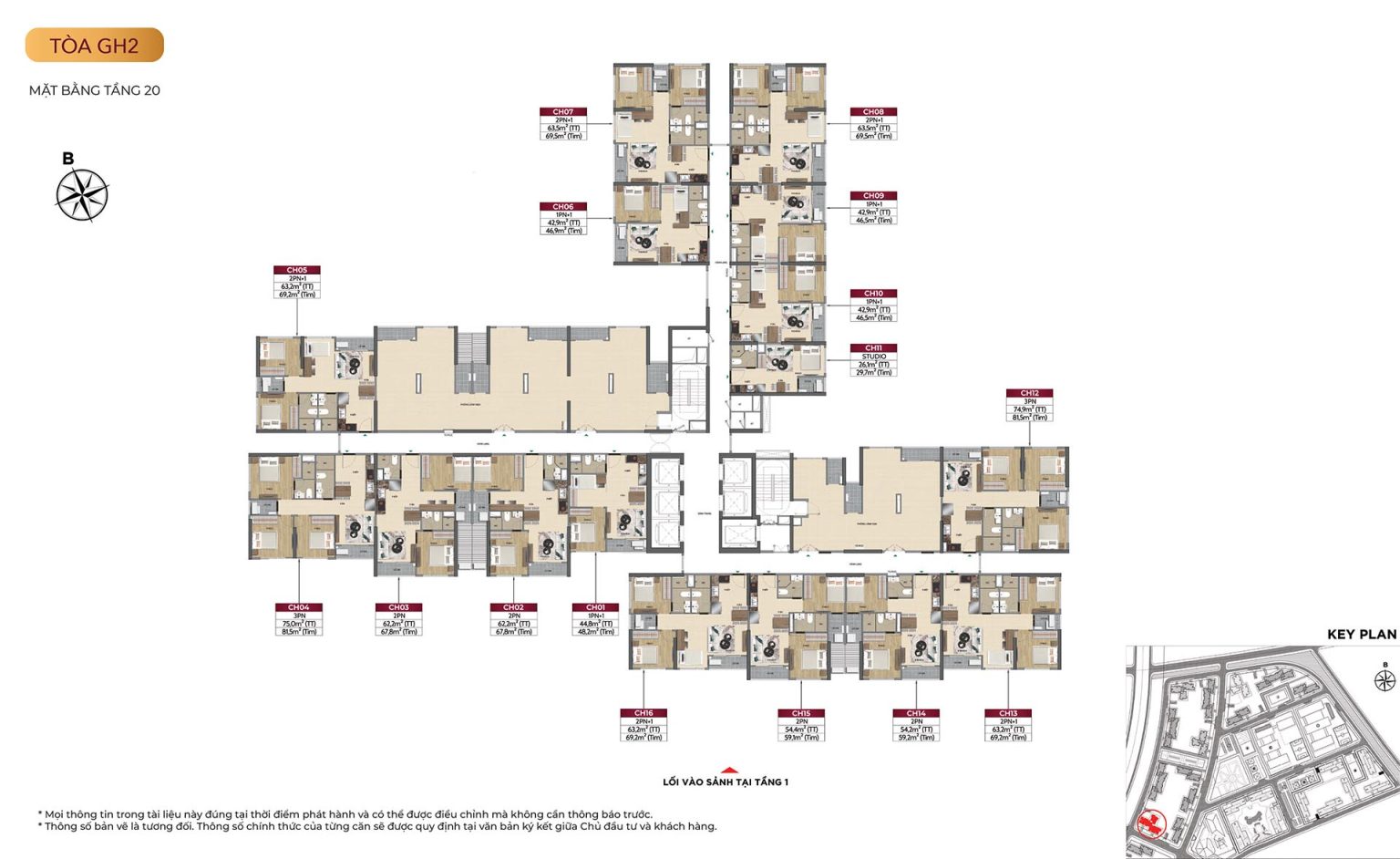
Mặt bằng tòa GH1
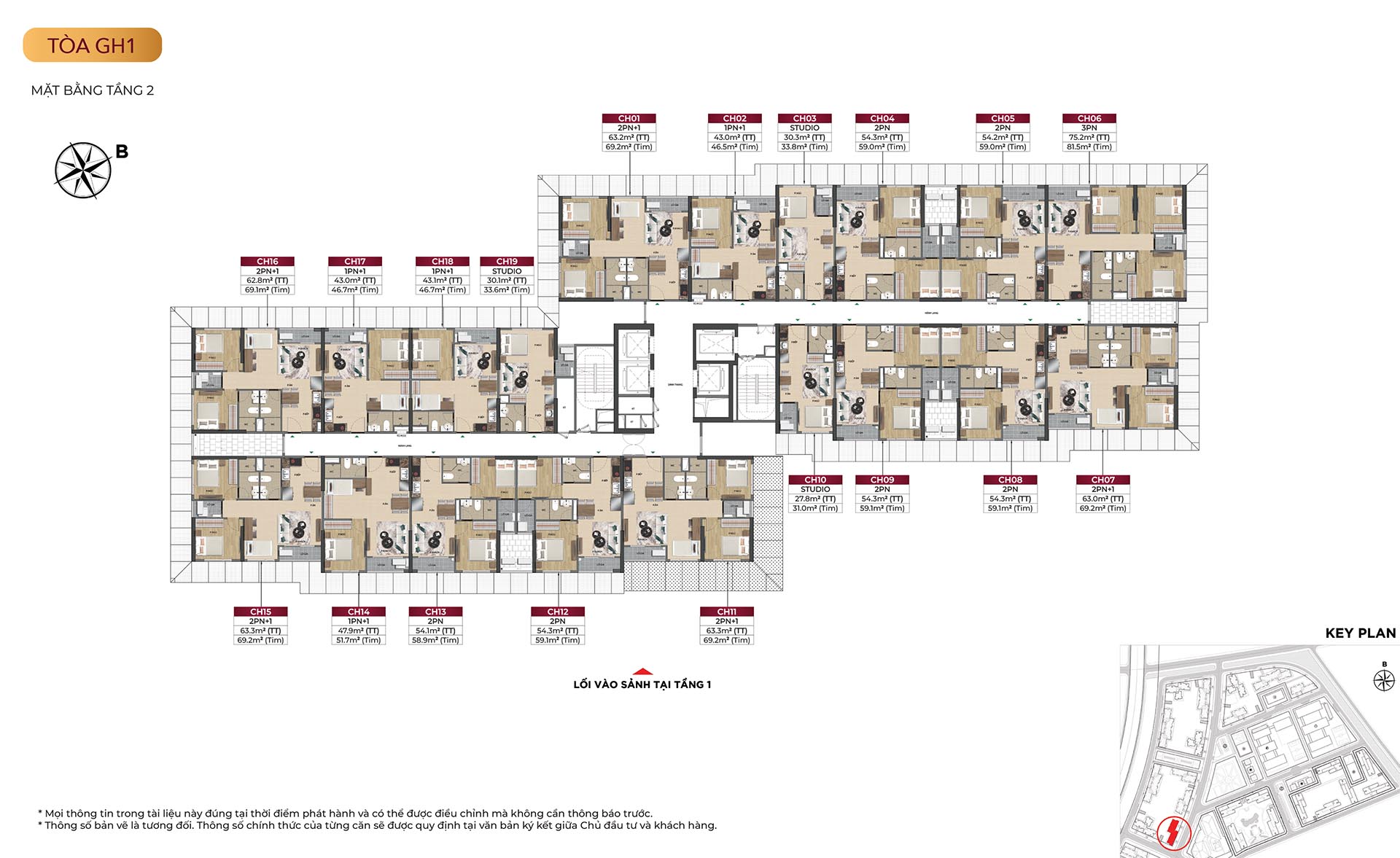
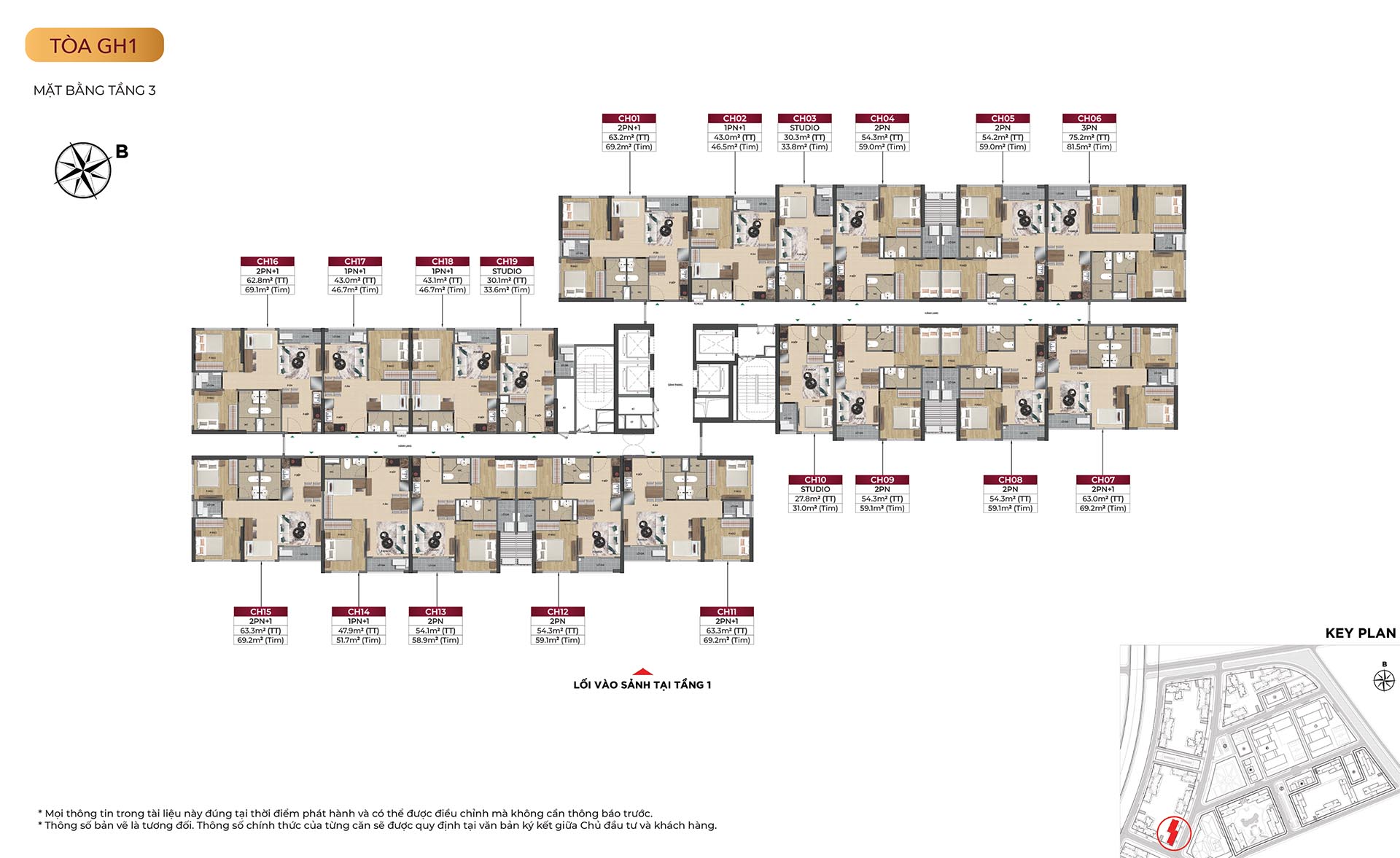
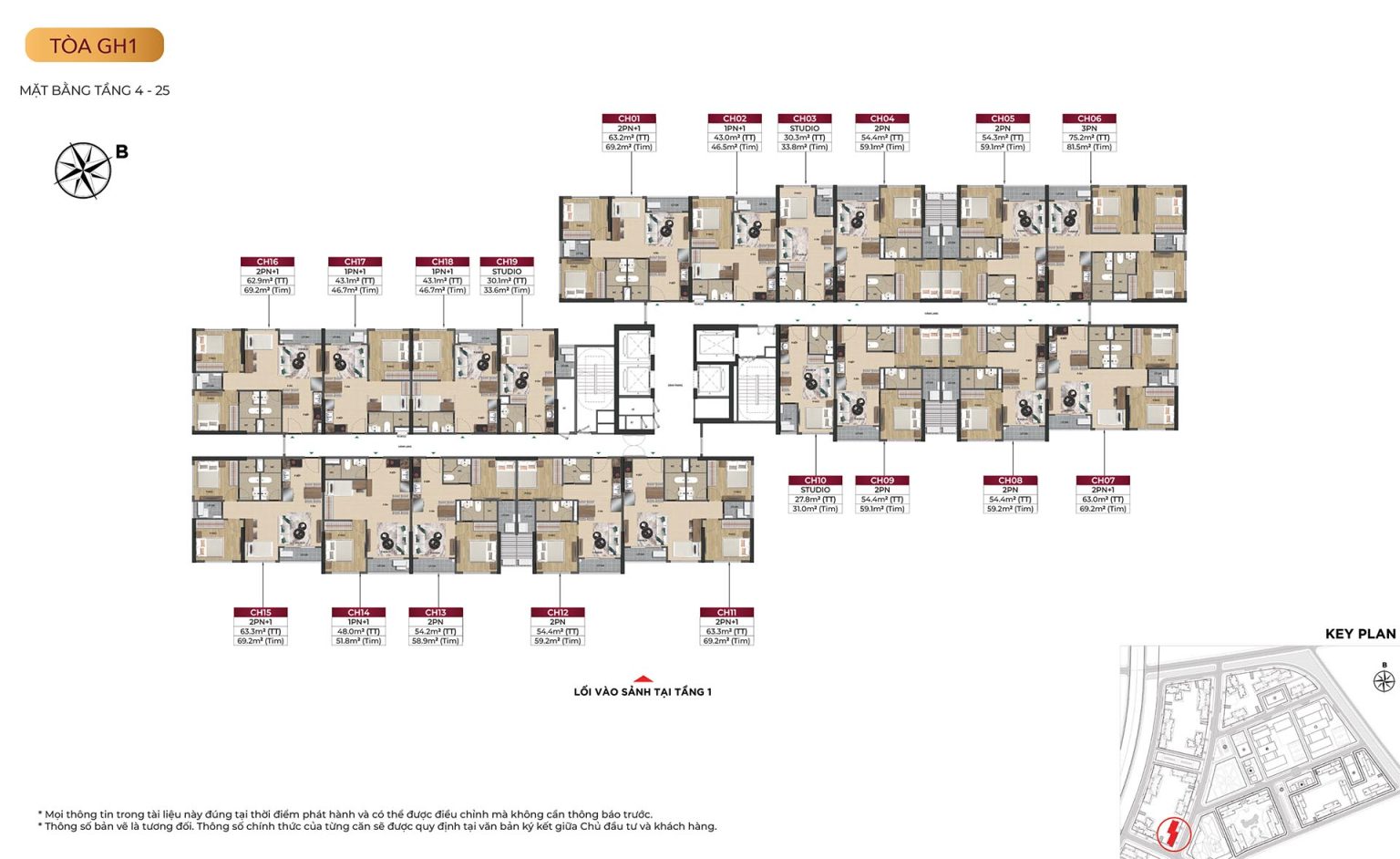
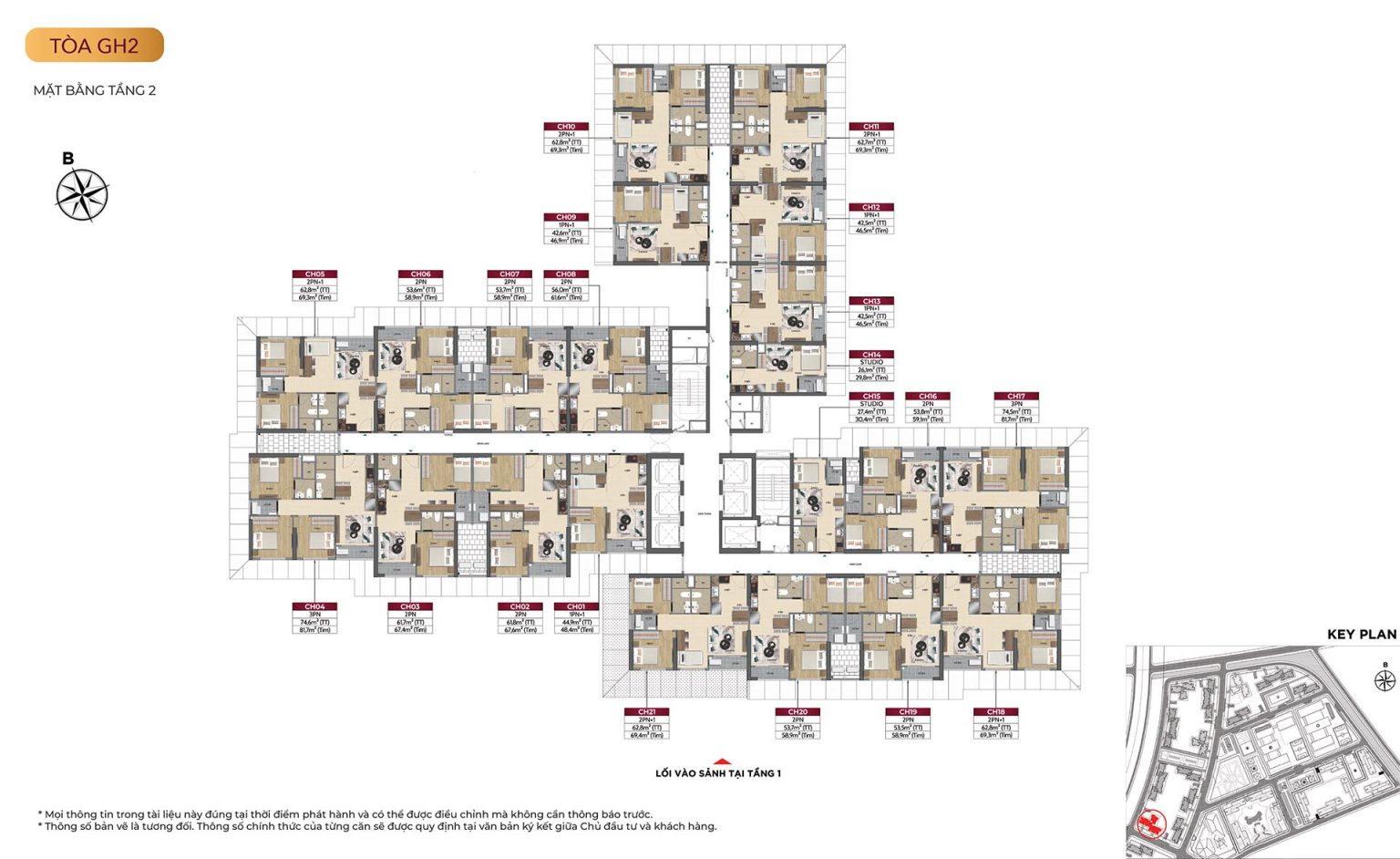
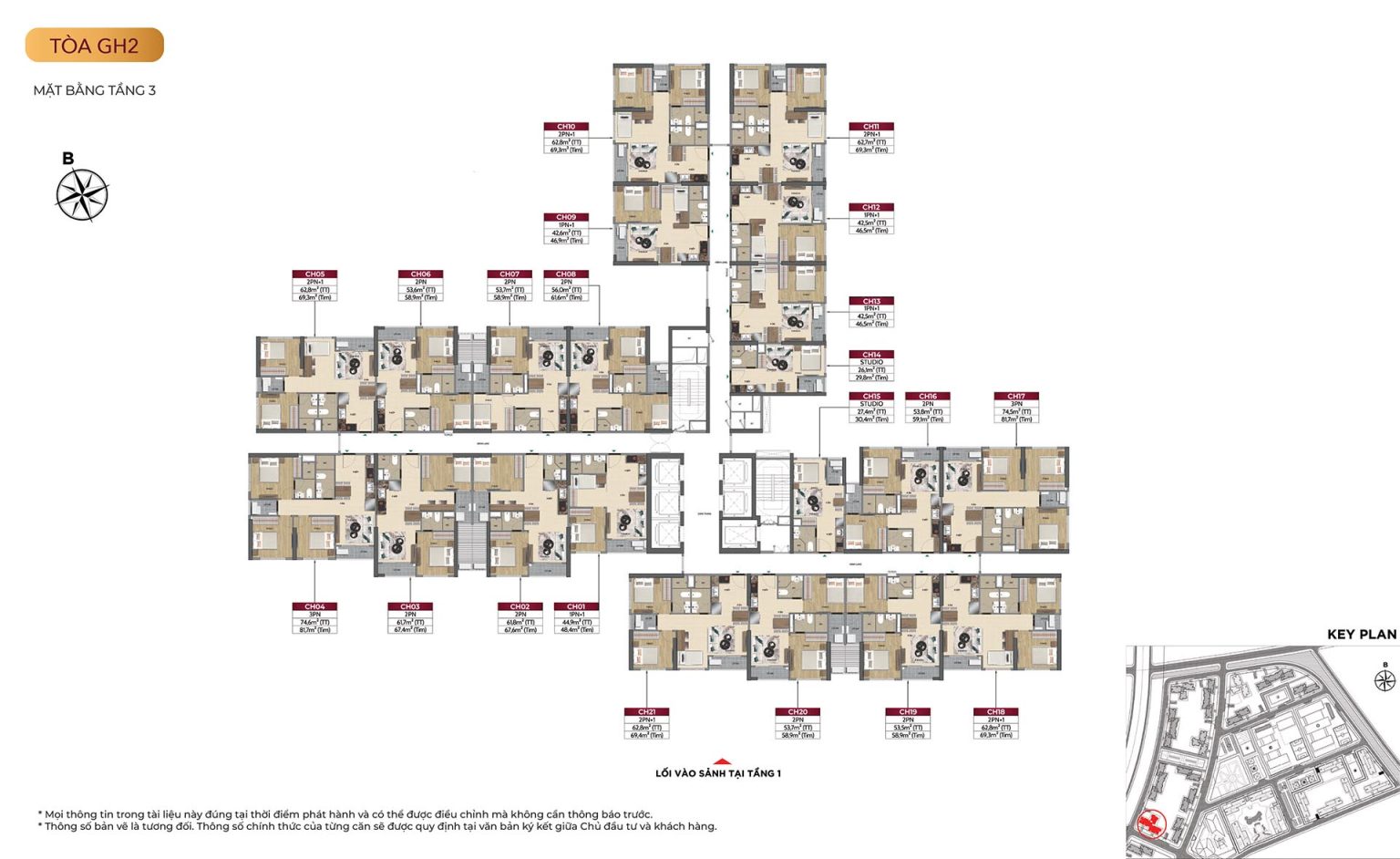
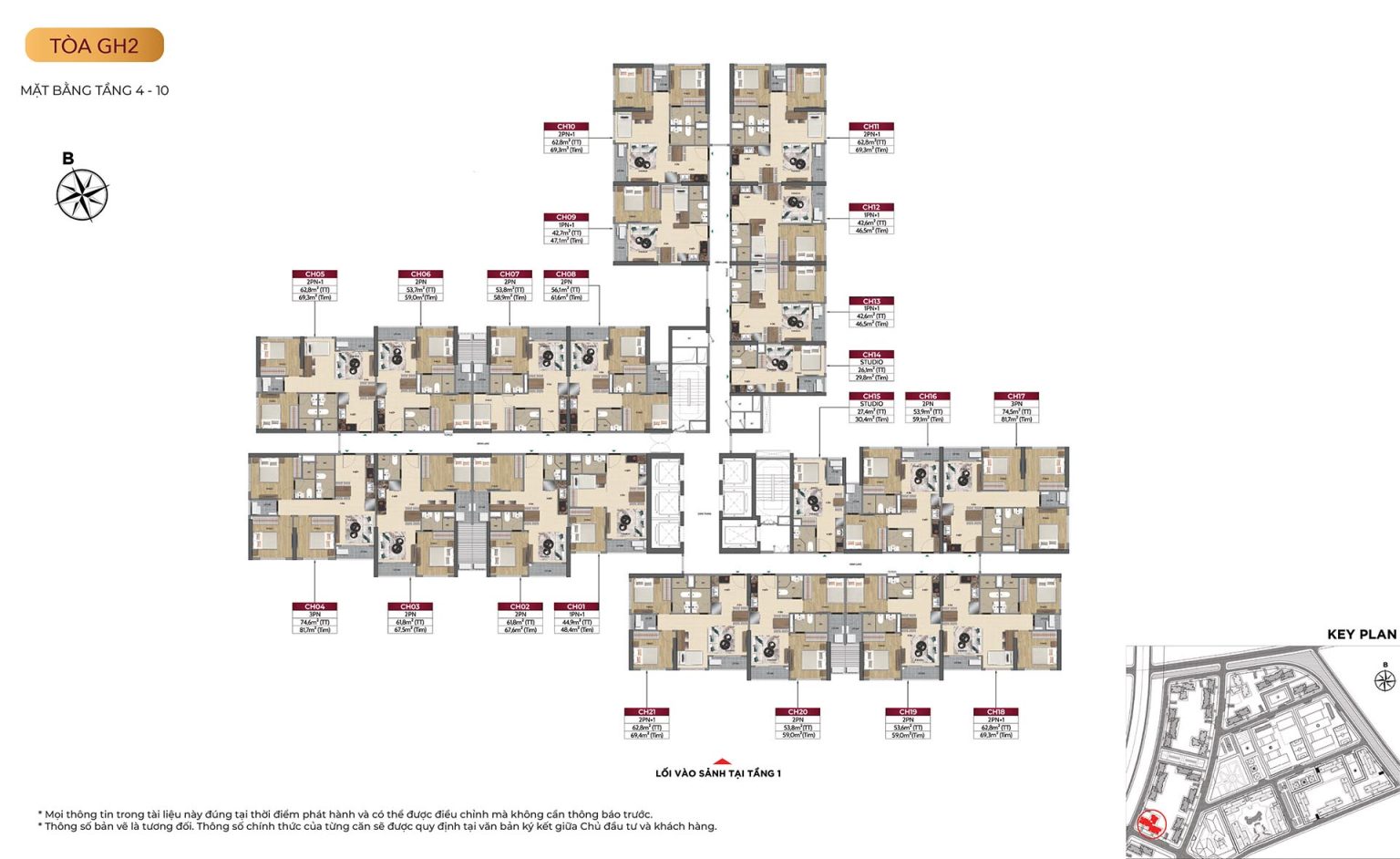
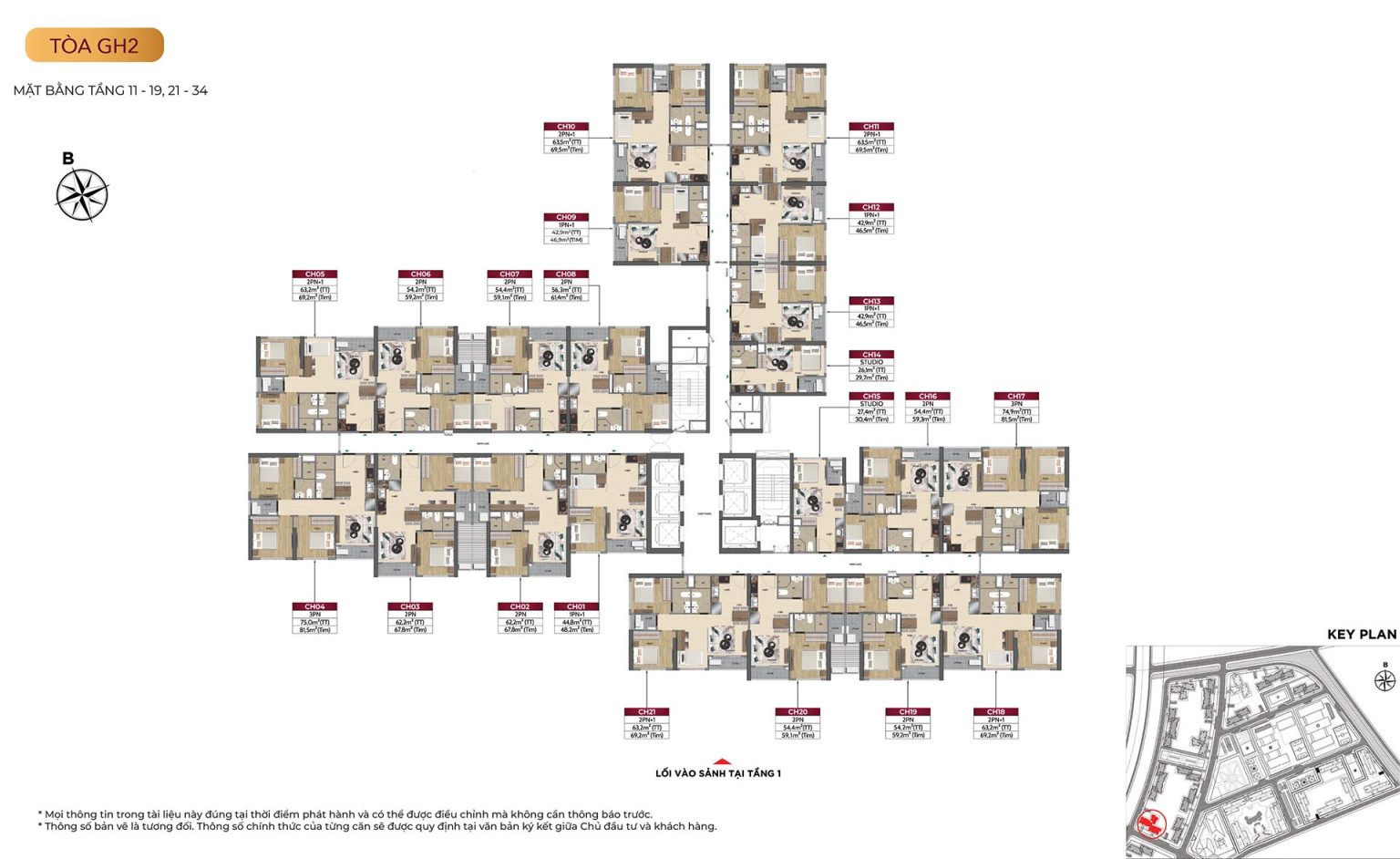
Mặt bằng tòa GH2
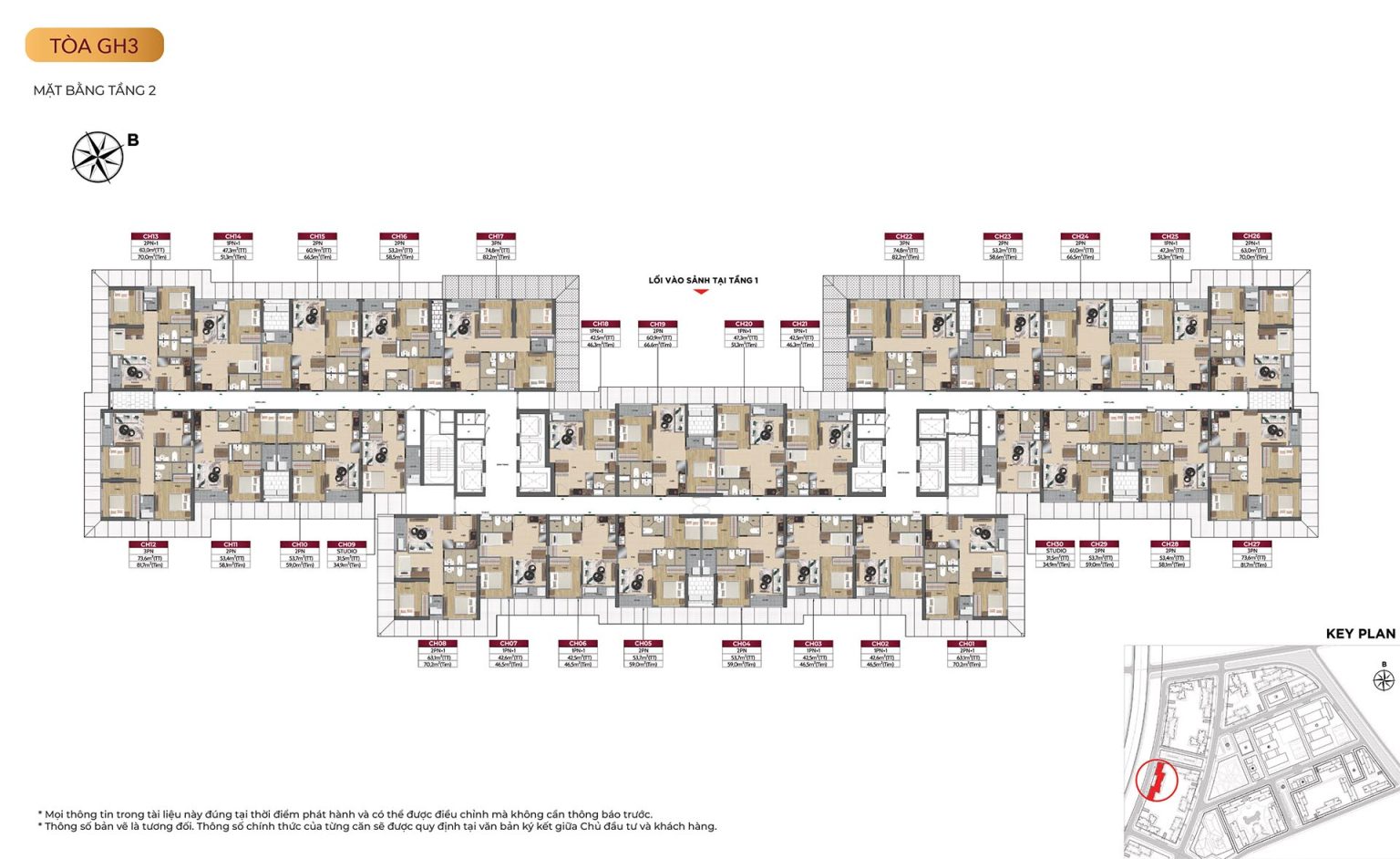
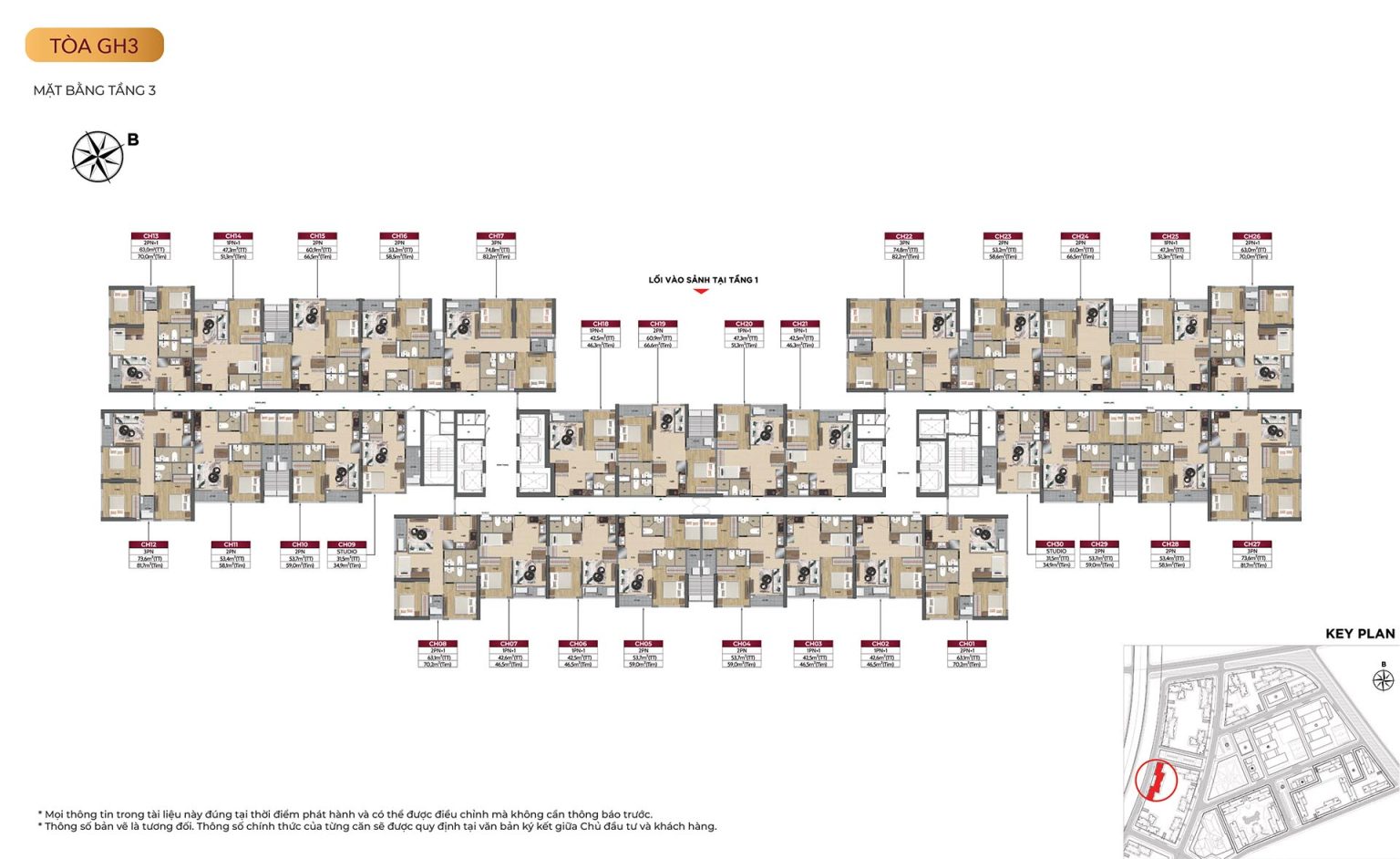
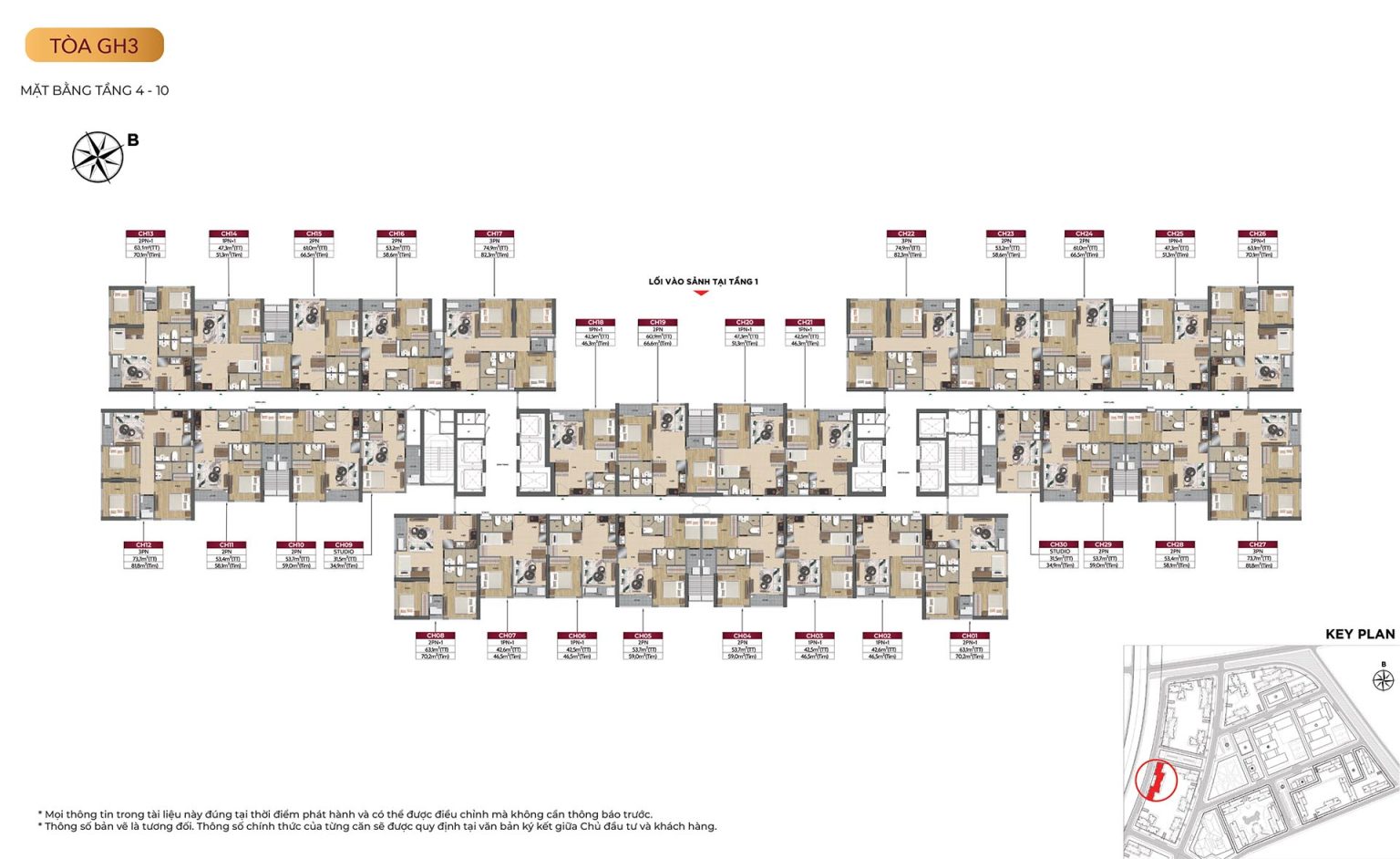
Mặt bằng tòa GH3
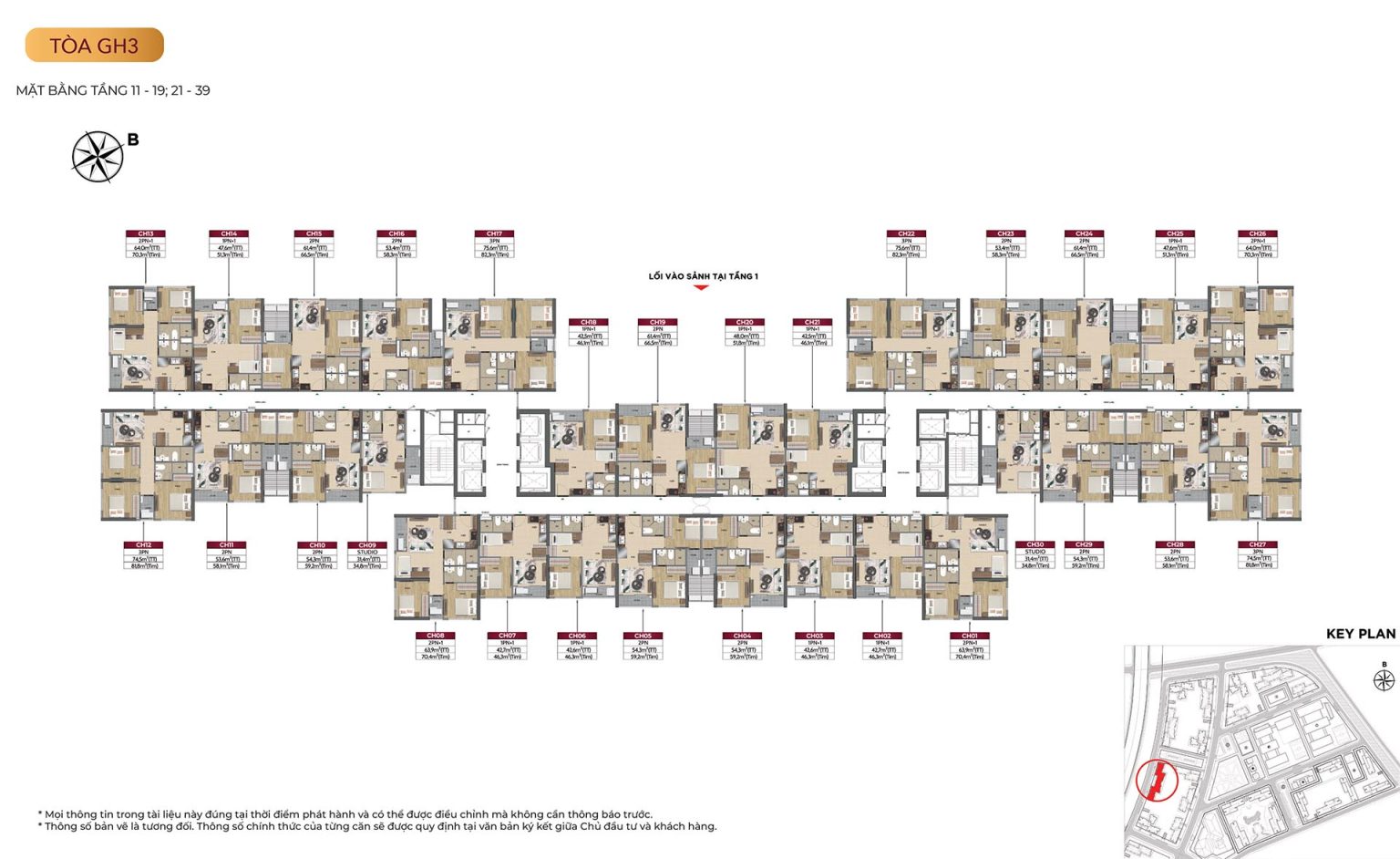
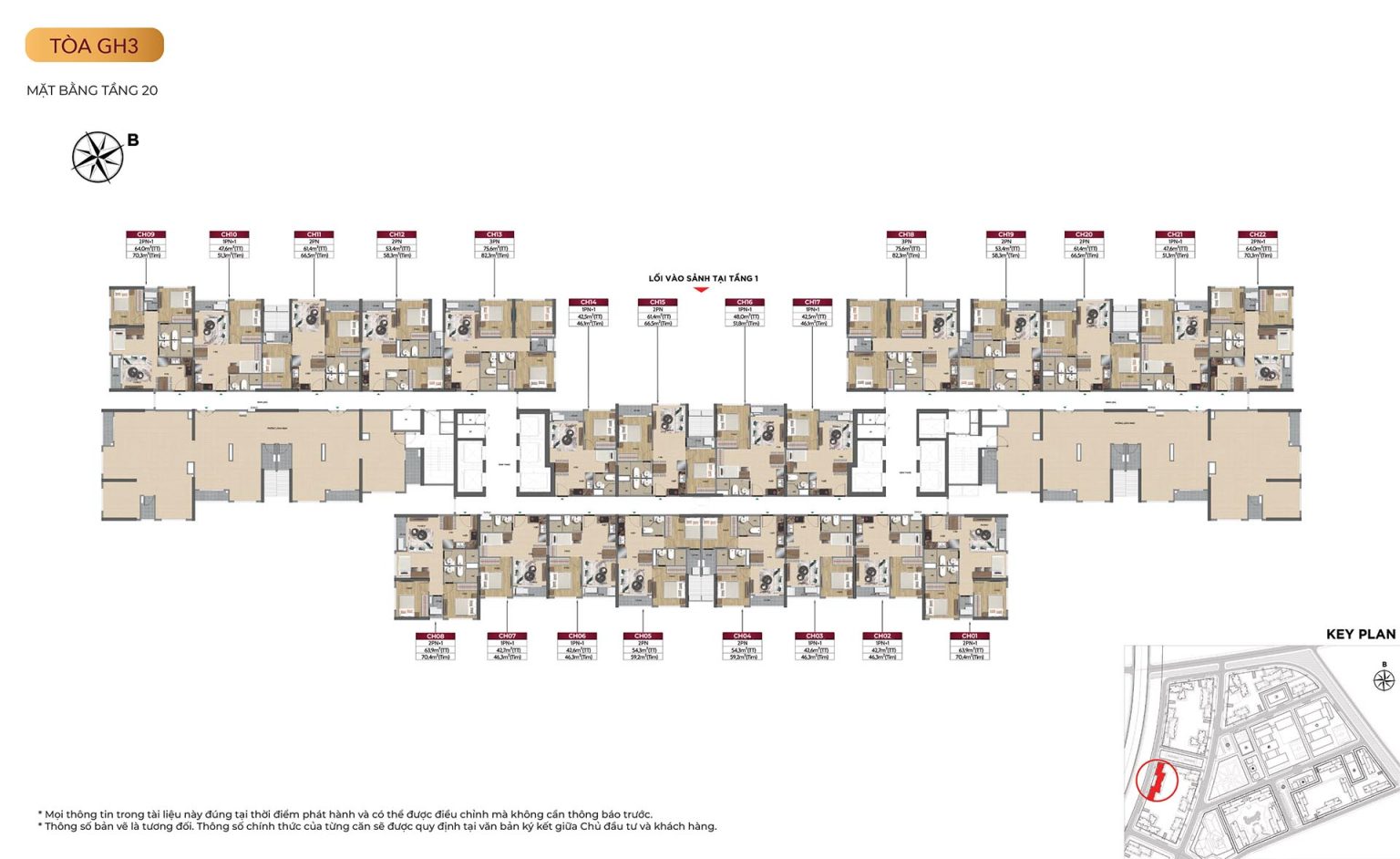
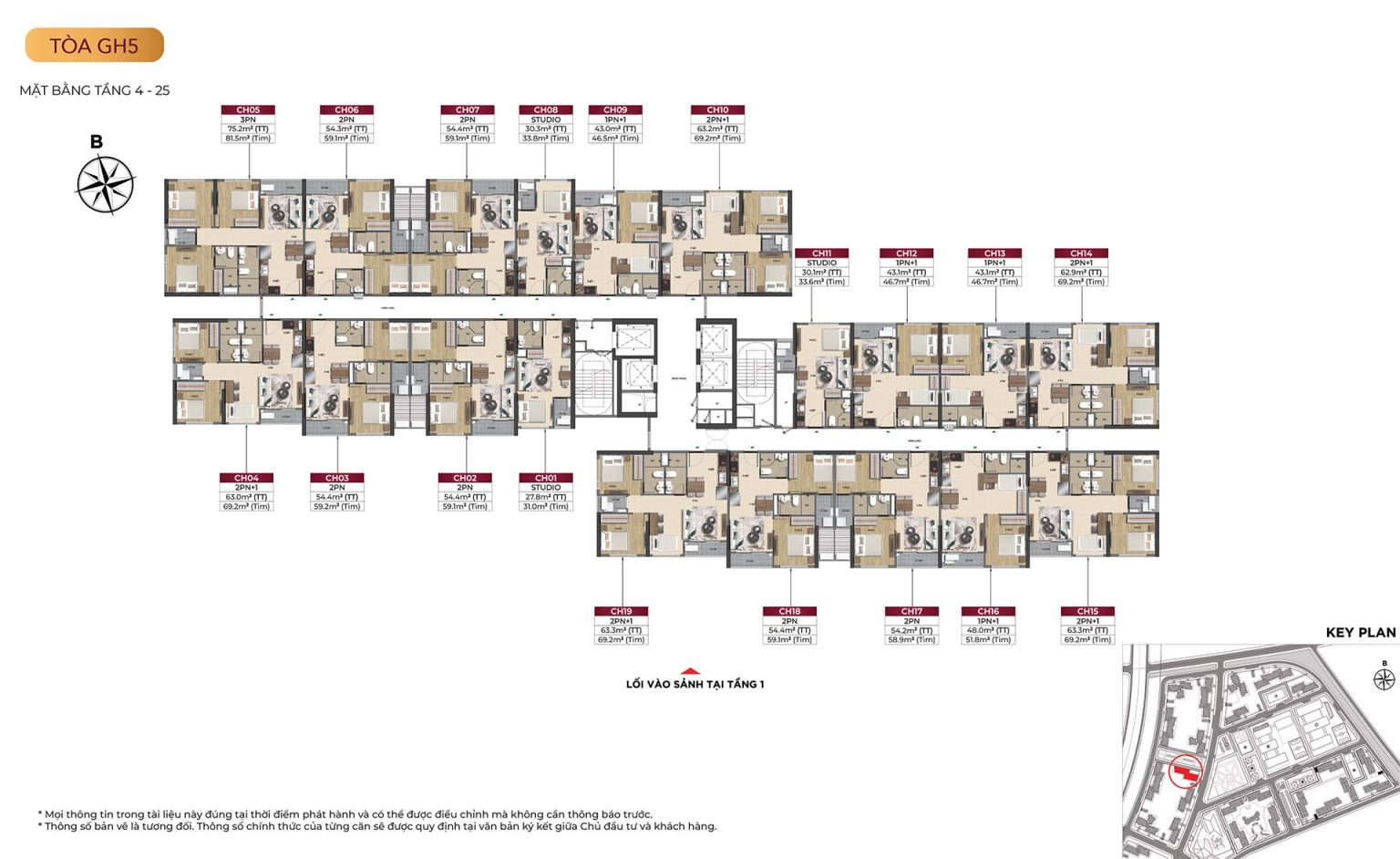
Mặt bằng tòa GH5
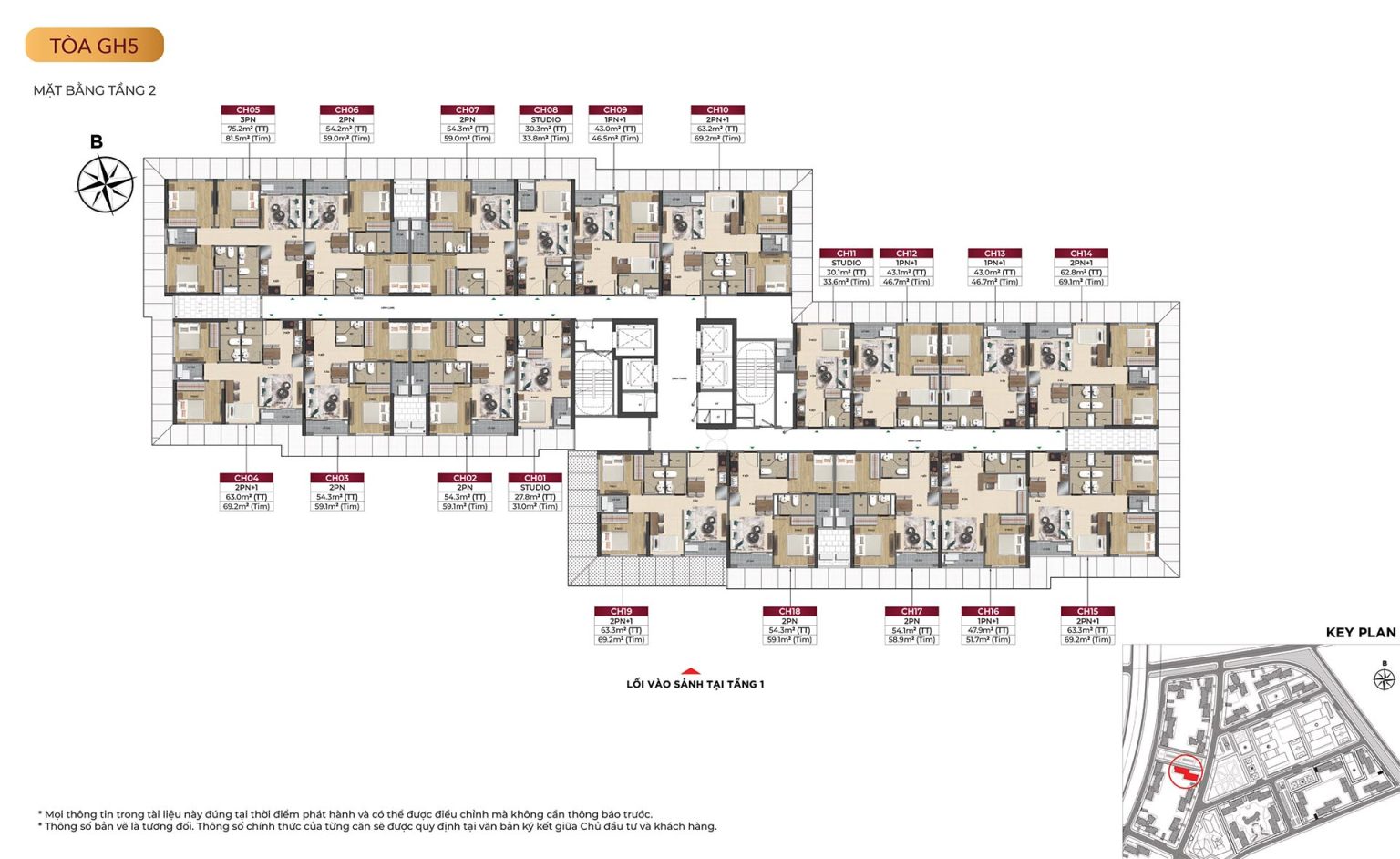
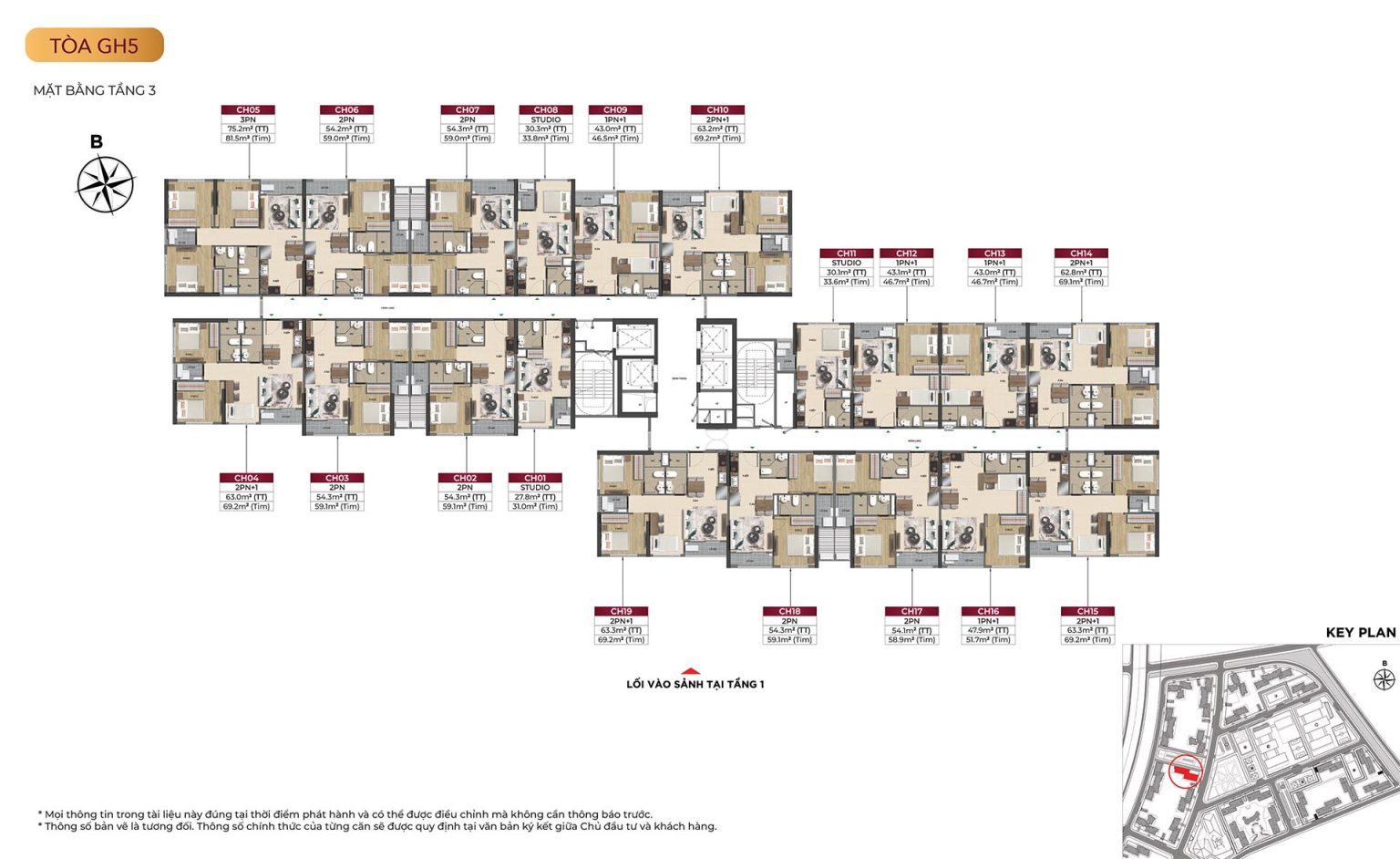
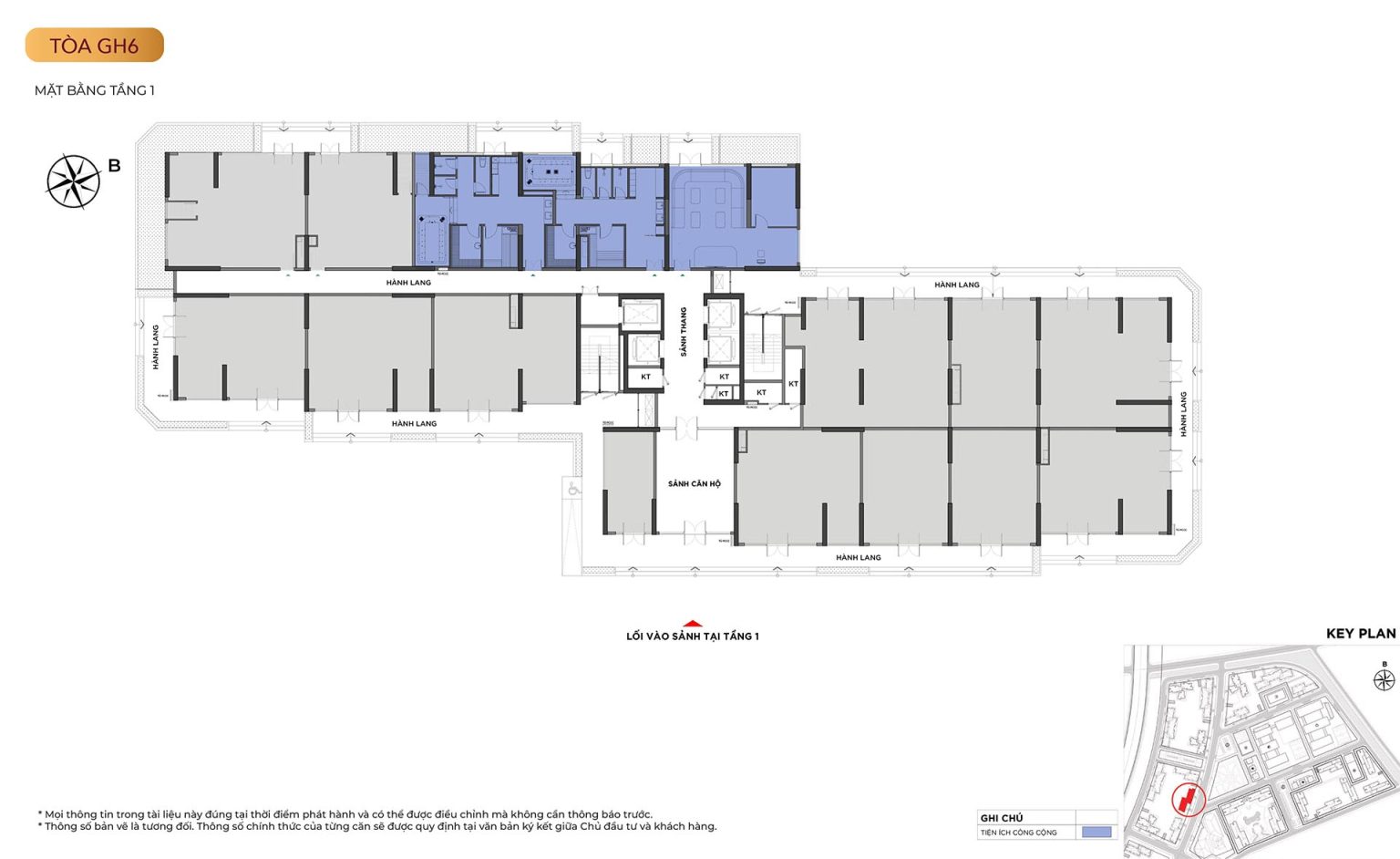
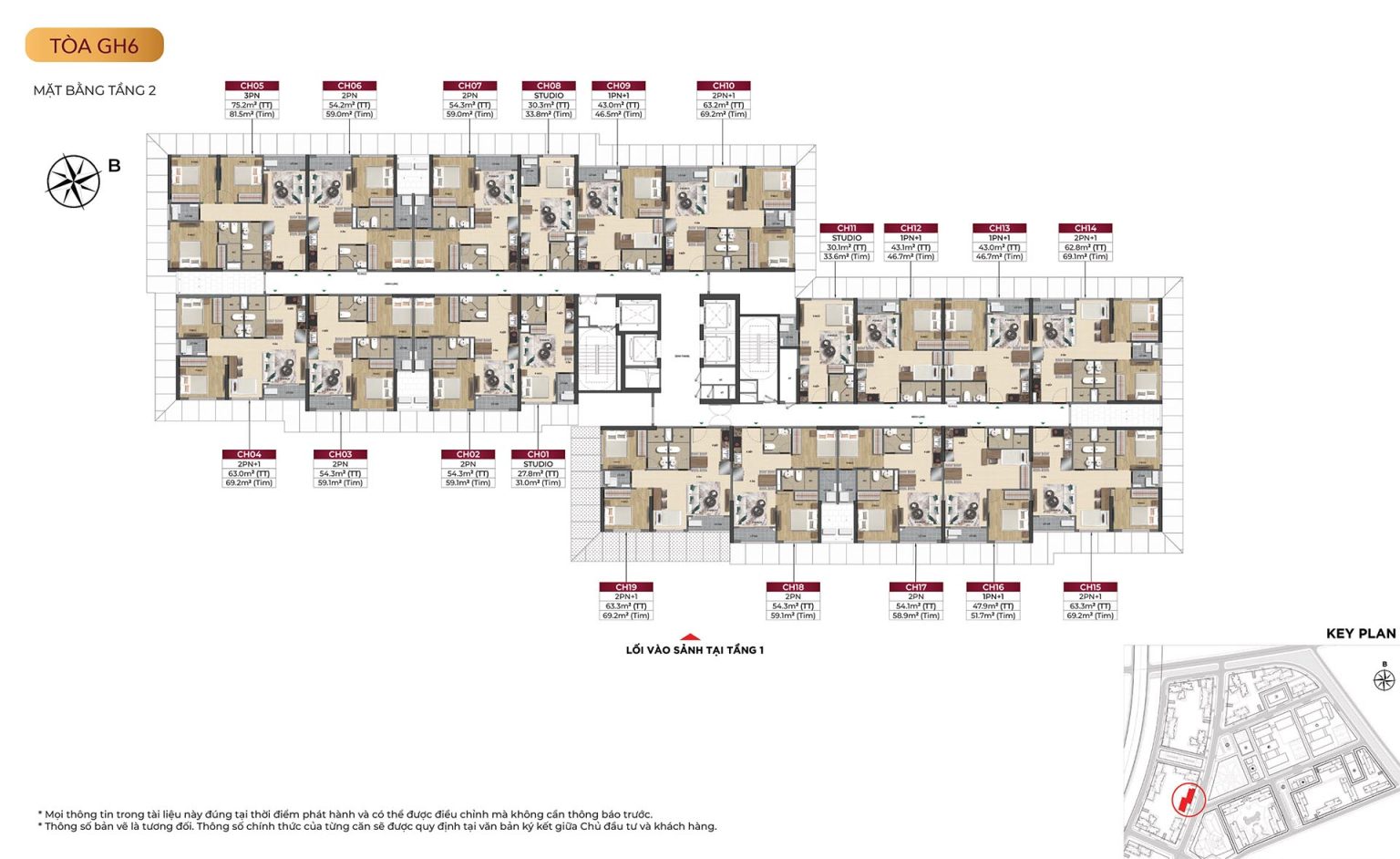
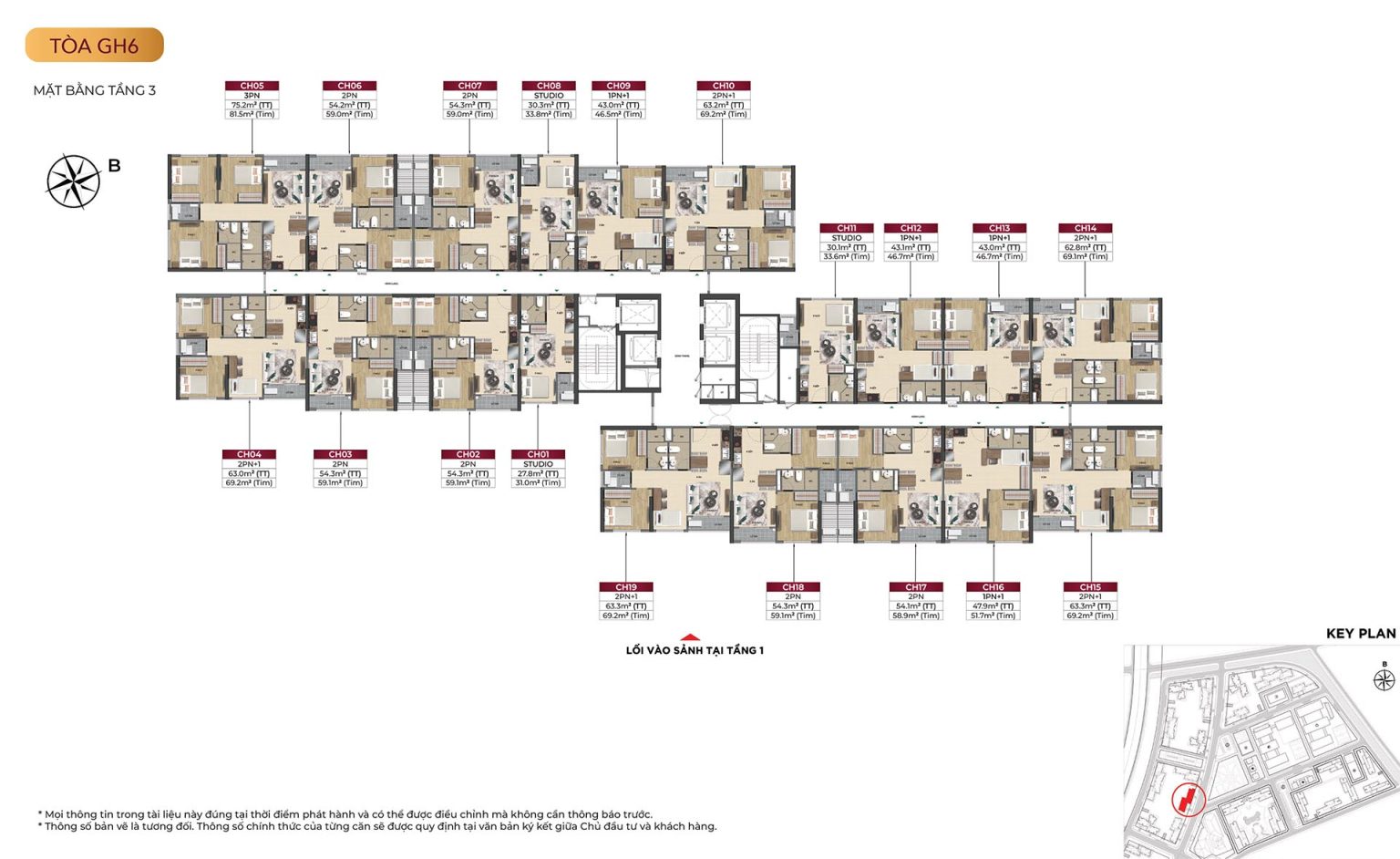
Mặt bằng tòa GH6
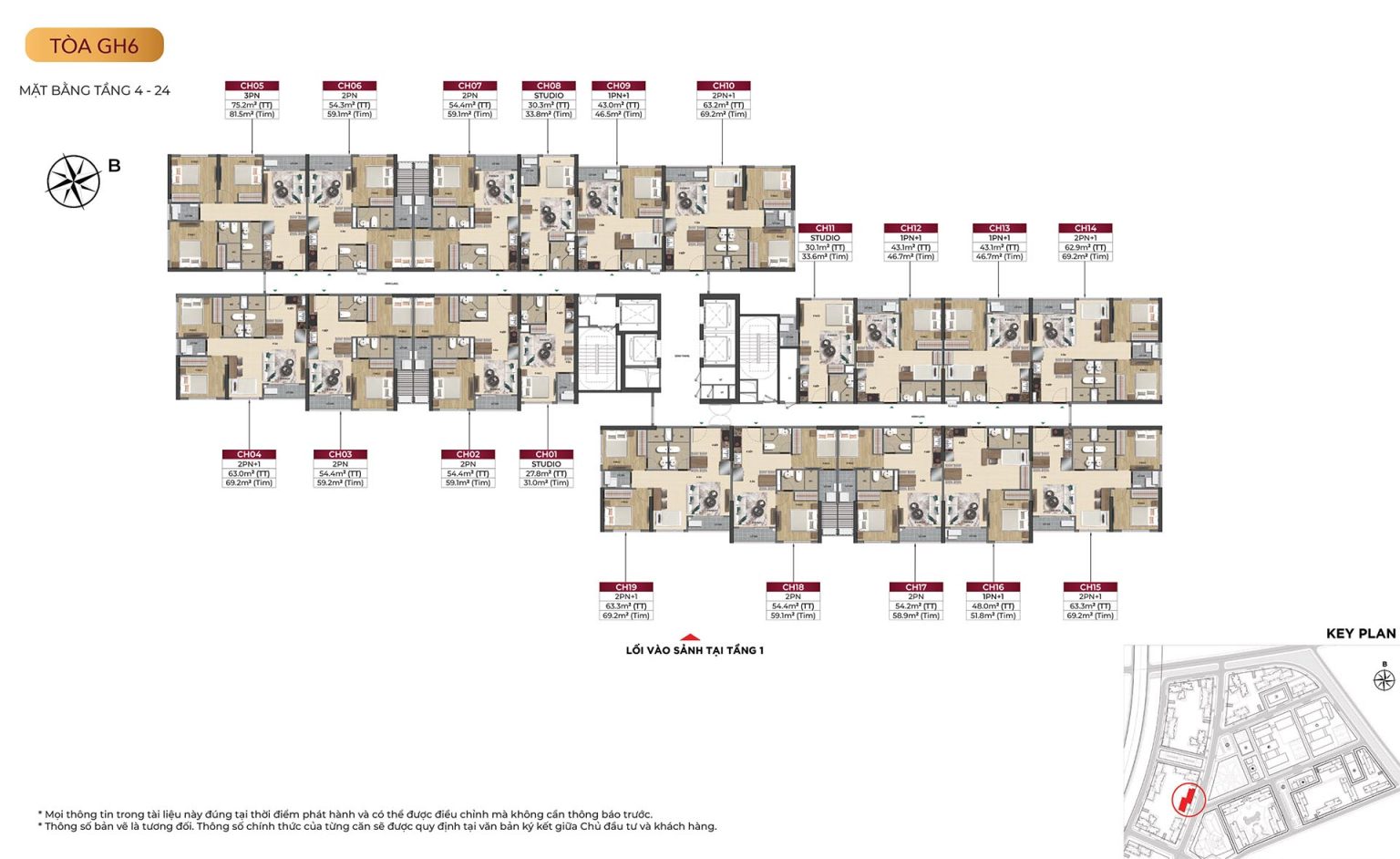

 |
 |
 |
 |
 |
 |
Glory Heights thuộc phân khu The Beverly Solari là một trung tâm độc đáo, các căn hộ được thiết kế với sự chú trọng đến chi tiết và cung cấp mọi tiện nghi cần thiết cho một cuộc sống thỏa mãn và tiện lợi.Không chỉ đẹp mắt, căn hộ tại Glory Heights còn được trang bị đầy đủ tiện nghi cao cấp, bao gồm trung tâm thể dục, hồ bơi, công viên và nhiều hơn thế nữa. Đồng thời, vị trí của dự án rất thuận lợi với việc kết nối với các khu vực quan trọng trong thành phố và các trung tâm giải trí, tạo nên một cuộc sống thuận tiện dành cho cư dân.
 |
 |
 |
 |
CHÍNH SÁCH “BOM TẤN”
CHỈ CÓ TẠI GLORY HEIGHTS
Với mức giá dự kiến từ 40 triệu/m2, các loại căn hộ tại Glory Heights có giá bán dự kiến:
- Căn Studio 30m2 chỉ từ 1,7 tỷ/căn
- Căn 1PN+ 46m2 chỉ từ 2,4 tỷ/căn
- Căn 2PN 60m2 chỉ từ 3 tỷ/căn
- Căn 2PN+ 70m2 chỉ từ 3,7 tỷ/căn
- Căn 3PN 81m2 chỉ từ 4,7 tỷ/căn
Không chỉ có mức giá dự kiến cực tốt với vị trí ngay tâm điểm thương mại Vinhomes Grand Park, căn hộ Glory Heights còn sở hữu chính sách bán hàng “Xứng tầm GUINNESS” với 03 CHÍNH SÁCH LINH HOẠT VÀ CHÍNH SÁCH “BOM TẤN”:
CHÍNH SÁCH 1: THANH TOÁN THẢNH THƠI 2 NĂM NHẬN NHÀ
Thanh toán chỉ 10% ký HĐMB
Thanh toán nhẹ nhàng 1,5%/tháng trong 2 năm
Thanh toán 45% nhận bàn giao
=> GIÁ BÁN CỰC TỐT

CHÍNH SÁCH 2: THANH TOÁN THẢNH THƠI 3 NĂM NHẬN NHÀ
Thanh toán chỉ 10% ký HĐMB
Thanh toán nhẹ nhàng 1%/tháng trong 3 năm
Thanh toán 45% nhận bàn giao
=> GIÁ BÁN CỰC TỐT

CHÍNH SÁCH 3: NHẬN NHÀ TRƯỚC THANH TOÁN SAU 2,5 NĂM
Thanh toán chỉ 10% ký HĐMB
Thanh toán chỉ 25% nhận bàn giao căn hộ
Ngân hàng hỗ trợ vay 70% lãi suất 0% TRONG 2.5 NĂM

CHÍNH SÁCH BOM TẤN: MUA NHÀ 7 NĂM KHÔNG LO LÃI SUẤT
Thanh toán chỉ 10% ký HĐMB
Thanh toán nhẹ nhàng 1%/tháng trong 3 năm
Nhận bàn giao căn hộ
NGÂN HÀNG HỖ TRỢ VAY 45% GTCH LÃI SUẤT 0% TRONG 4 NĂM

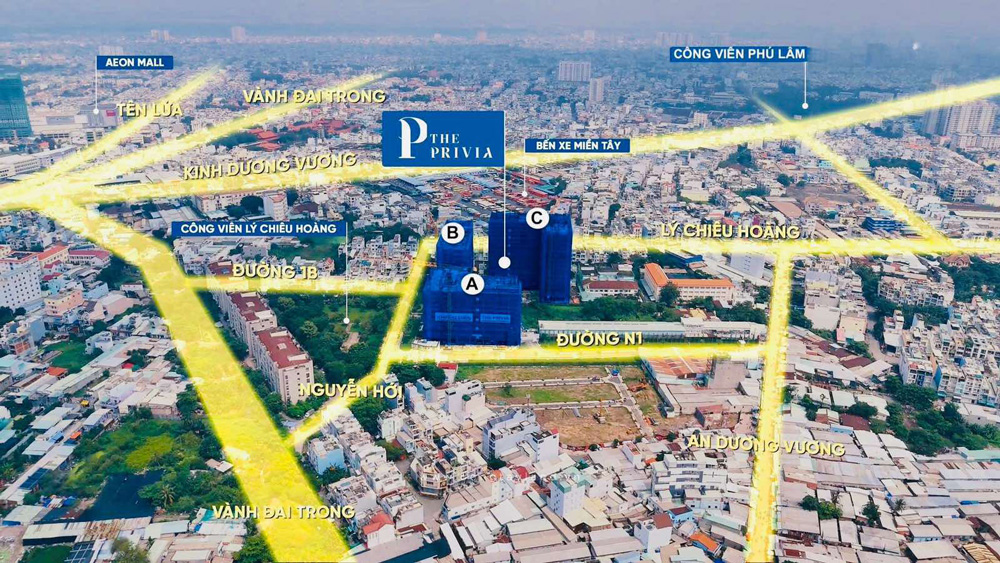
THE PRIVIA BÌNH TÂN
Khang Điền mở bán đợt 1 The Privia Tháng 11/2023
Siêu phẩm Privia chào quý 4/2023. Dự án đang trong giai đoạn Rumour và nhận booking mở bán giai đoạn 1 với giá bán trong khoảng dự kiến từ 48 – 50 triệu đồng/m2. Khách hàng sở hữu sản phẩm tại dự án để ở, đầu tư tại ngay tâm điểm của thị trường khu Tây Hồ Chí Minh sẽ được cho ra mắt vào thời gian tới với sự bố trí hài hòa của các tòa tháp căn hộ.

THE PRIVIA KHANG ĐIỀN
-
Tên dự án: The Privia
-
Vị trí: Số 158 đường An Dương Vương, phường An Lạc, quận Bình Tân, thành phố Hồ Chí Minh
-
Đơn vị phát triển: Tập đoàn Khang Điền
-
Tổng diện tích: 1,83 ha
-
Quy mô: 1.043 căn hộ
-
Khuôn viên tiện ích: Công viên, siêu thị, hồ bơi, phòng sinh hoạt cộng đồng, nhà trẻ, khu vui chơi giải trí, quán café, …
-
Chủ đầu tư dự án: Công ty TNHH MTV ĐT KD Nhà Khang Phúc. Hose: KDH (Thành viên tập đoàn Khang Điền)
-
Thời gian bàn giao dự kiến: Quý 4/2024
- Đơn vị phân phối : Hunter Land

Tọa lạc trên đường An Dương Vương, thuộc KDC hiện hữu sầm uất tại P.An Lạc – Q.Bình Tân, kết nối đa chiều với nhiều trục giao thông huyết mạch. Từ dự án, chỉ 20 phút về trung tâm Q.1 theo Đại lộ Võ Văn Kiệt, nhanh chóng di chuyển đến Q.5, Q.10, Q.3 theo đường Kinh Dương Vương, thuận tiện về miền Tây qua Quốc lộ 1A.
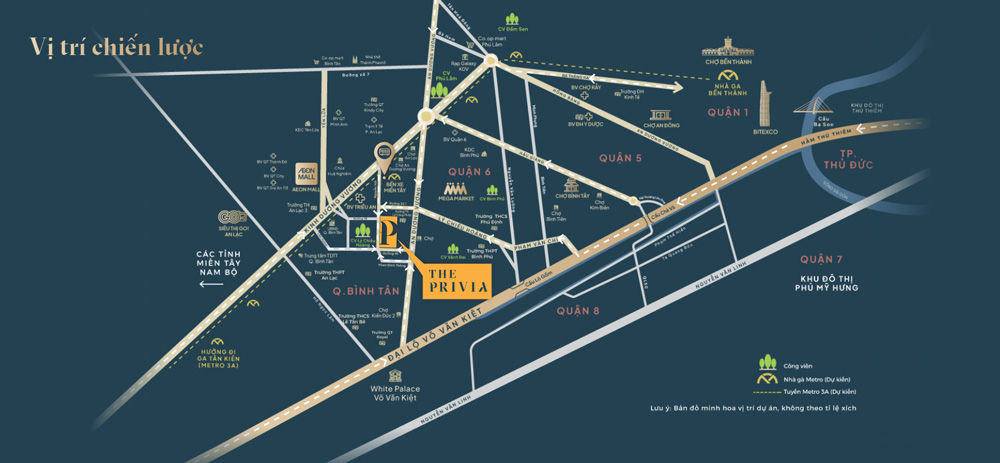
The Privia tọa lạc tại mặt tiền đường An Dương Vương, số địa chỉ 158, P. An Lạc, Q. Bình Tân. Đây là vị trí giáp ranh giữa Q. Bình Tân và Quận 6, là trung tâm sầm uất bậc nhất khu Tây Sài Gòn.
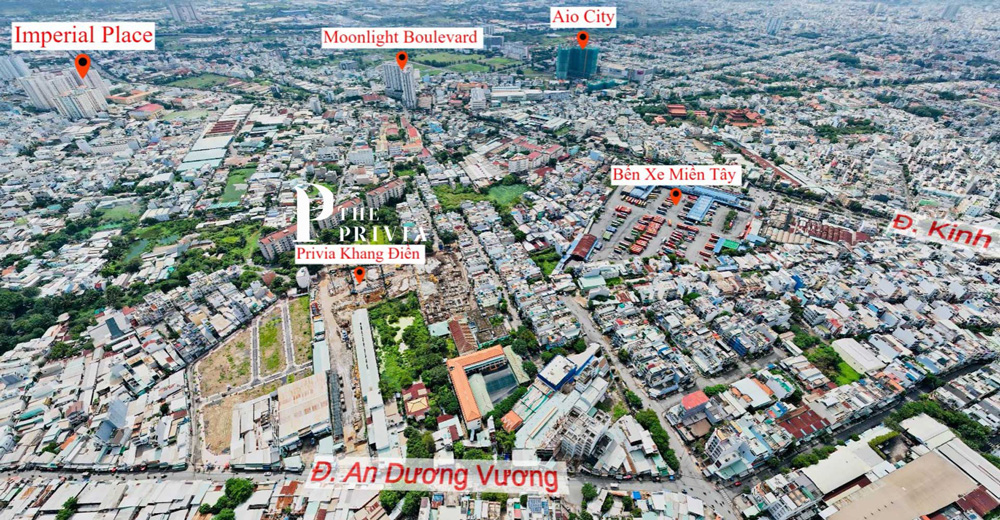
Từ căn hộ The Privia cư dân chỉ mất:
5 phút: Bến xe Miền Tây, MM Mega Market, Aeon Mall, Galaxy Kinh Dương Vương, công viên Phú Lâm, công viên Bình Phú, bệnh viện Gia An, Chi cục thuế quận Bình Tân, UBND phường An Lạc, trường THPT Bình Phú, bệnh viện quốc tế Minh Anh, bệnh viện Gia An 115, BV quốc tế City,..
10 phút: Big C An Lạc, UBND quận Bình Tân, bệnh viện Đa Khoa Bình Tân, chợ Phú Lâm, trường Trung học An Lạc, Công viên văn hóa Đầm Sen, Khu Công nghiệp Tân Tạo.

15 phút: Đại học Y Dược, Đại học Kinh tế, Đại học Sư Phạm, Đại học Bách Khoa, bệnh viện Y Dược, bệnh viện Nhiệt Đới, bệnh viện 115, bệnh viện Chợ Rẫy, bệnh viện Nhi Đồng, bệnh viện Hùng Vương.
20 phút: Các quận trung tâm như: Quận 1, Quận 3, Quận 10,…
Tiện ích nơi ngưỡng cửa
Với mong muốn nâng tầm trải nghiệm sống cho cư dân. Tại The Privia, hệ thống tiện ích được chăm chút tỉ mỉ và bố trí xen lẫn nhiều mảng xanh tạo nên một tổng thể hài hòa duy mỹ.

Sôi động cùng dãy thương mại dịch vụ (Shophouse) kinh doanh các mặt hàng đa dạng; tăng cường trải nghiệm nghỉ dưỡng với hệ thống tiện ích đủ đầy: hồ bơi xanh mát, sân chơi trẻ em, phòng gym, phòng yoga, phòng đọc sách,… Tất cả, sẽ đan xen cùng nhau thỏa niềm vui rèn luyện sức khỏe, tận hưởng khoảnh khắc sum vầy và tìm về với hạnh phúc an nhiên!

Khu căn hộ The Privia Bình Tân không những khẳng định đẳng cấp từ vị trí tọa lạc mà còn từ điều kiện tiện ích hiện đại, đáp ứng đa dạng nhu cầu của cư dân trong đời sống sinh hoạt và vui chơi giải trí.

Dự án sở hữu hồ bơi riêng, đường dạo bộ, phòng tập Gym và phòng Yoga là nơi quý khách hàng có thể thoải mái vận động, rèn luyện thể chất với những trang thiết bị tiên tiến, hiện đại. Bên cạnh đó, khu vực shop house và siêu thị mini cung cấp các mặt hàng từ thiết yếu đến xa xỉ phục vụ nhu cầu mua sắm đa dạng của tầng lớp dân cư.

Bảo chứng cho một nơi an cư đáng tin cậy chính là dịch vụ quản lý tòa nhà vận hành chuyên nghiệp, xử lý các vấn đề phát sinh một cách nhanh chóng. Cùng với đó là hệ thống an ninh an toàn được đảm bảo 24/7 với rào chắn, bảo vệ tuần tra và camera an ninh.

Ngoài những tiện nghi trong khuôn viên dự án, cư dân Chung cư The Privia Khang Điền còn đường hưởng lợi từ vô vàn công trình tiện ích ngoại khu hiện hữu do nằm ở tâm điểm kinh tế – văn hóa của quận Bình Tân. Các tiện ích về thương mại – dịch vụ như: chợ Vải, chợ Sắt, chợ Bình Tây, chợ An Đông, …. Về giáo dục như: Đại học Bách Khoa, Đại học Sư Phạm, …. Và về y tế như: bệnh viện Chợ Rẫy, bệnh viện Y Dược, bệnh viện 115, ….

Nhìn chung với chuỗi tiện ích này, cư dân không còn phải lo lắng về chất lượng cuộc sống tại Dự án The Privia . So với nhiều dự án cùng phân khúc tại Bình Tân, căn hộ The Privia Khang Điền quả thực xứng đáng là một trong những nơi an cư lý tưởng

Dự án căn hộ The Privia Khang Điền Bình Tân nằm ngay mặt tiền đường lớn An Dương Vương và đường nội bộ thuộc ô chức năng số 1 từ đường An Dương Vương và đường Nguyễn Hới. Nhờ lợi thế của mình mà dự án đã dễ dàng khai thác thương mại tại các sản phẩm căn shophouse khối đế.

Ngoài ra, dự án còn nằm ngay trong khu dân cư ổn định nên có tầm view ngoài rộng rãi, thoáng đãng và không bị che chắn bởi các dự án cao tầng khác.
The Privia mang thiết kế độc đáo với bố cục hình chữ U, bao gồm 3 tháp: A, B và C. Tất cả các tháp đều hướng về phía Đông và được bố trí sao cho có khoảng cách giữa chúng, tạo điều kiện thuận lợi cho việc đối lưu gió tự nhiên.
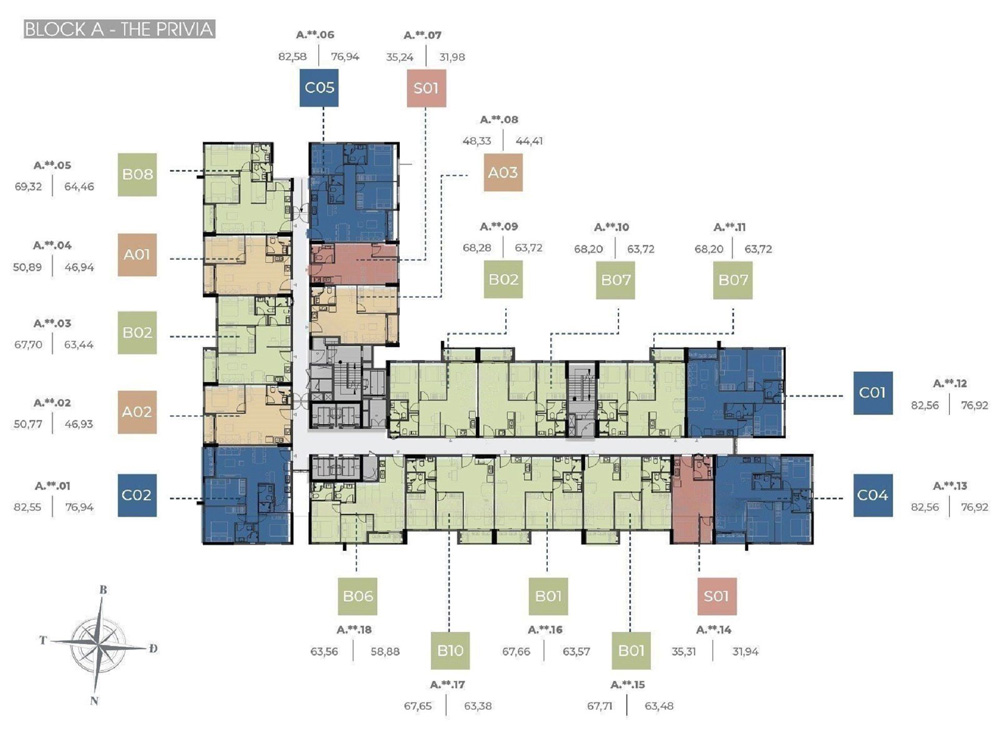
Tháp A: Bố trí 18 căn hộ trên mỗi tầng, với 4 thang máy dành cho khách và 1 thang hàng. Thiết kế theo hình chữ L, bắt đầu từ tầng 4 và gồm: 2 căn studio, 3 căn 1 phòng ngủ mở rộng, 9 căn 2 phòng ngủ mở rộng, và 4 căn 3 phòng ngủ.
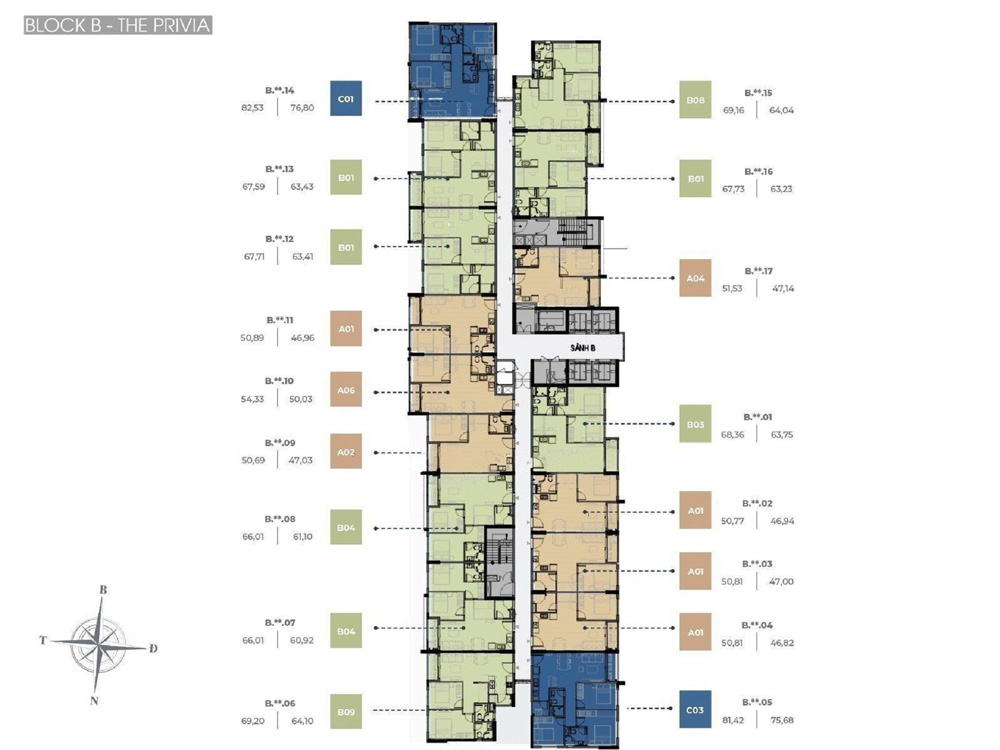
Tháp B: Đặc trưng với 17 căn hộ mỗi tầng, cũng bao gồm 4 thang máy cho khách và 1 thang hàng. Mang thiết kế hình chữ I, và bắt đầu từ tầng 5: 7 căn 1 phòng ngủ mở rộng, 8 căn 2 phòng ngủ mở rộng và 2 căn 3 phòng ngủ.
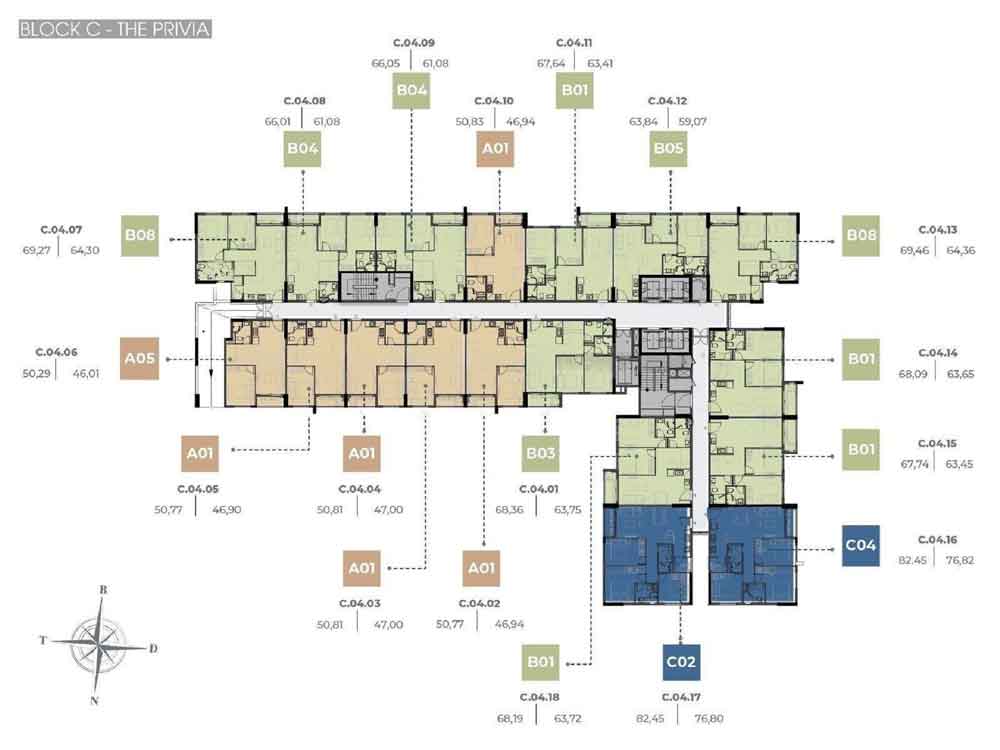
Tháp C: Giống như Tháp A, Tháp C có 18 căn hộ trên mỗi tầng và được thiết kế theo hình chữ L. Mỗi tầng bao gồm: 5 căn 1 phòng ngủ mở rộng, 11 căn 2 phòng ngủ mở rộng, và 2 căn 3 phòng ngủ
Dự án The Privia Khang Điền tập trung vào không gian sống xanh, với mật độ xây dựng thấp. Đa phần diện tích được dành riêng cho các tiện ích và khu vực sinh hoạt cộng đồng, đáp ứng tiêu chuẩn cao cấp cho cư dân.
Các căn hộ mặc dù nằm trong khu dân cư hiện hữu nhưng có tầm nhìn rất thông thoáng, không bị che chắn bởi các công trình cao tầng khác. Kết hợp với thiết kế thông minh, bài bản bên trong, The Privia được kỳ vọng sẽ mang đến không gian sống rộng rãi, thoáng mát cho gia đình gia chủ.
The Privia Khang Điền Bình Tân được thiết kế đạt tiêu chuẩn cao cấp theo phong cách kiến trúc và nội thất phương Tây. Khách hàng có nhiều sự lựa chọn về loại hình căn hộ có diện tích từ 35m² – 52m² – 66m² – 68m² – 85m².
Tùy theo nhu cầu, tầm tài chính mà khách hàng có thể lựa chọn các căn hộ có từ 1-3PN được bố trí xây dựng riêng biệt theo từng tòa tháp khác nhau. Bố trí quy hoạch, thiết kế các căn hộ tinh tế; hiện đại giúp tối ưu hóa công năng cũng như tích hợp không gian sống cho mọi gia đình.
Các loại hình sản phẩm căn hộ khách hàng có thể lựa chọn sở hữu gồm:
-
-
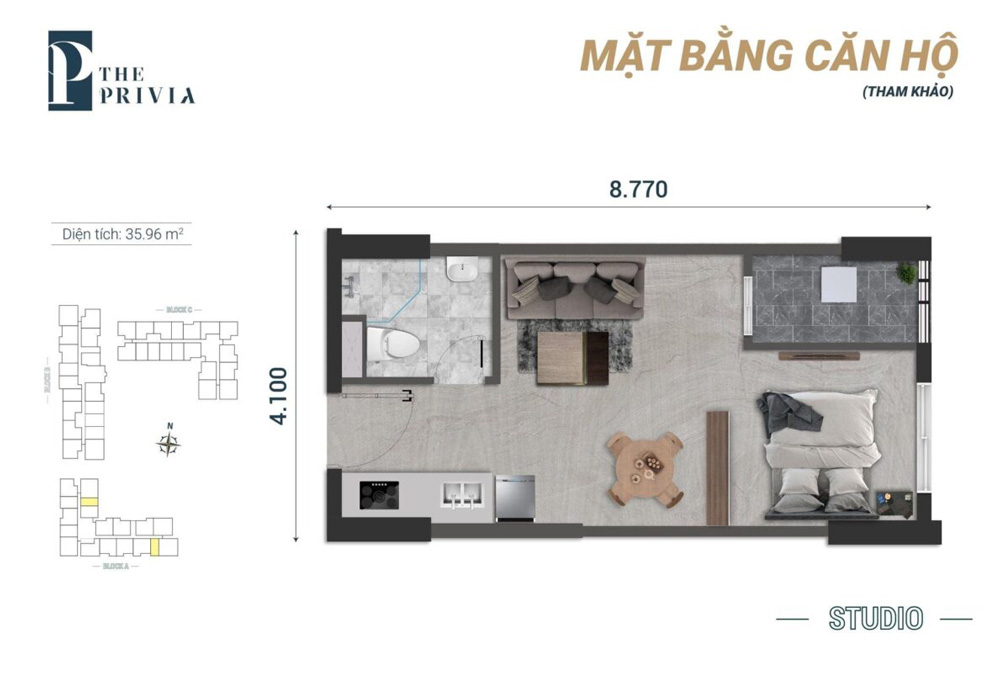
- ✅ Căn hộ studio : 35.96m²
-
- ✅ Căn hộ 1PN+1 : 50 – 51.74m²
- ✅ Căn hộ 2PN+1 : 66.29 – 68.66m²
- ✅ Căn hộ 2PN+1 (căn góc) : 71.41 – 71.63m²
- ✅ Căn hộ 3PN : 83.84 – 84.89m²
MẶT BẰNG CHI TIẾT CĂN HỘ
Căn hộ Studio :
Căn hộ 1PN+ :
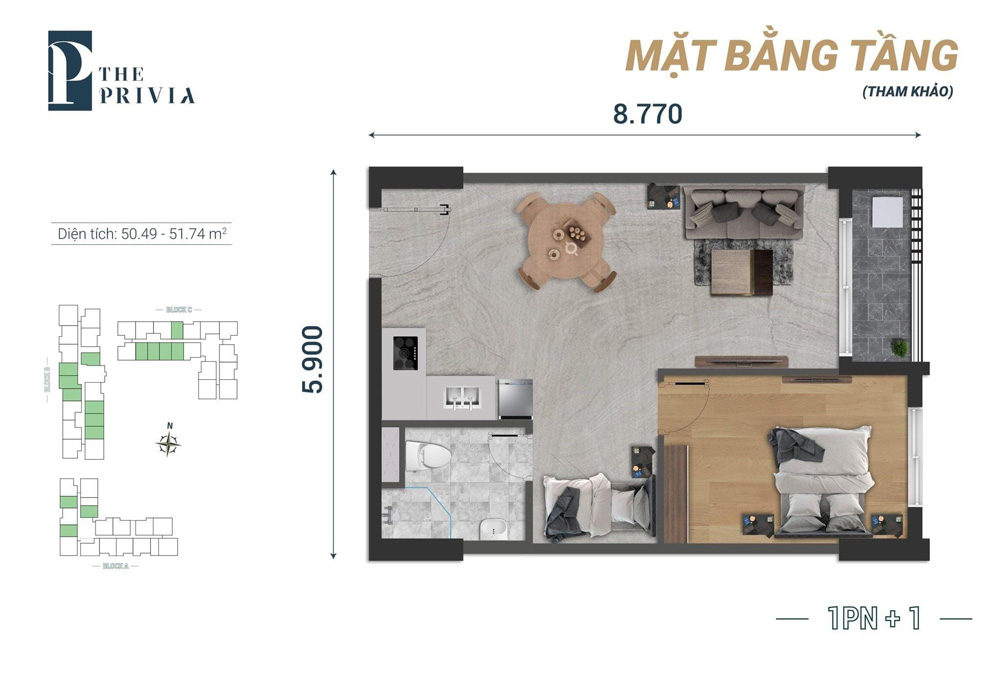
Căn hộ 2PN :
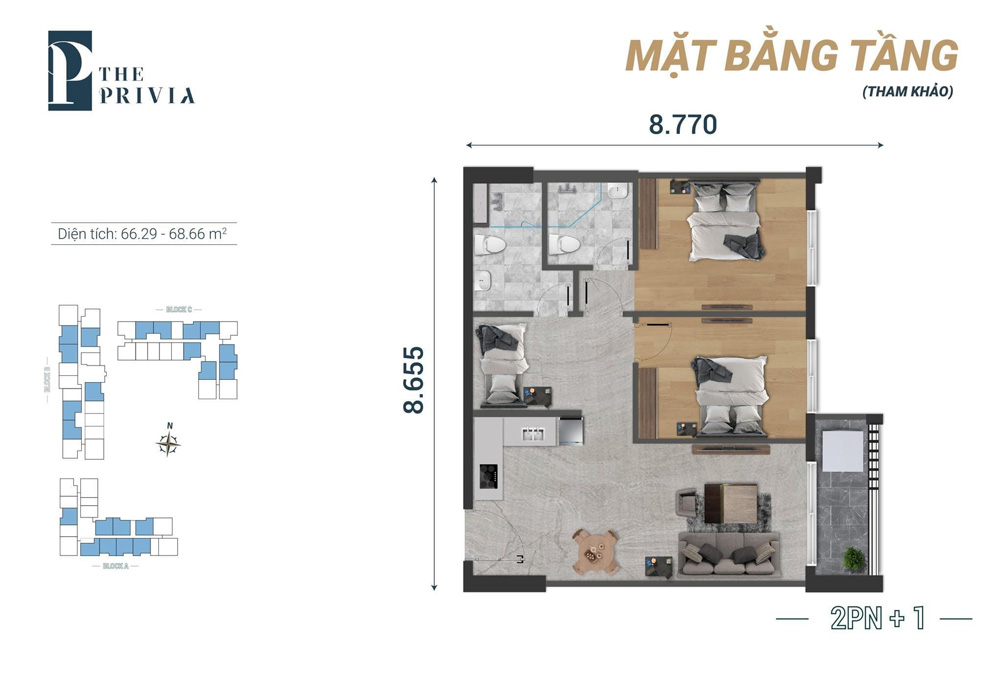
Căn hộ 2PN+1 :
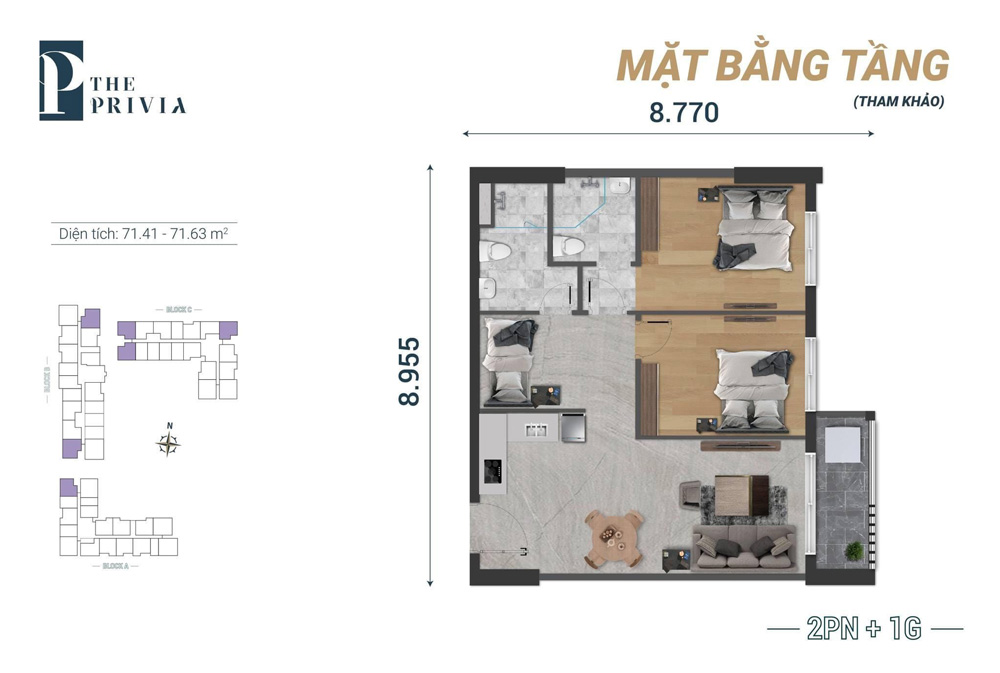
Căn hộ 3PN :
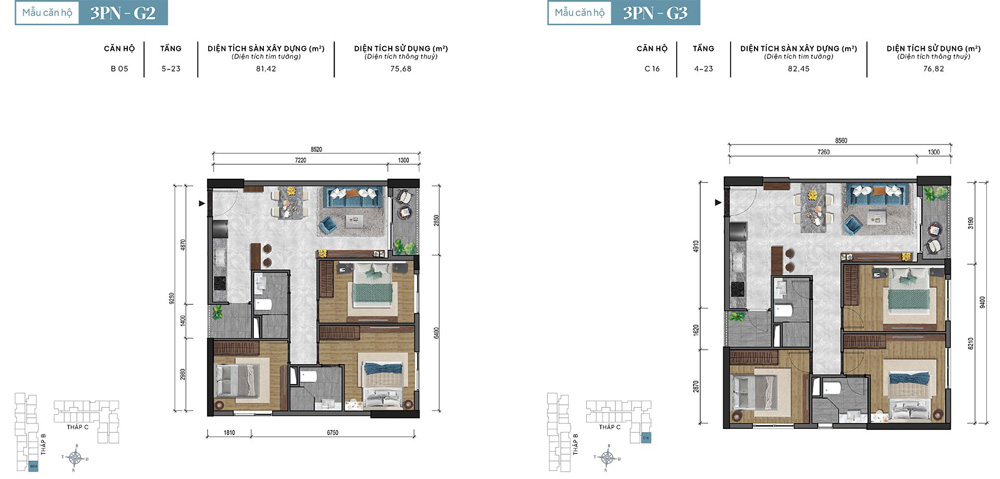
Danh mục vật liệu bàn giao :
- Khoá từ: HAFELE
- Cửa chính: Cửa gỗ chống cháy MDF
- Sàn phòng khách: gạch Porcelain - Sàn phòng ngủ: sàn gỗ công nghiệp 12mm
- Thiết bị vệ sinh: Hafele
- Thiết bị bếp: tủ bếp trên - dưới, kính ốp bếp - Kính cường lực 5mm, mặt đá bếp dưới - đá tự nhiên, chậu rửa và vòi- MALLOCA
Dự Án Privia được trang bị nội thất đẳng cấp, sang trọng. Các thương hiệu cao cấp được xuất hiện tại dự án đạt tiêu chuẩn quốc tế đem lại sự hiện đại; tiện nghi và giúp đảm bảo tính sạch đẹp, sáng sủa cho ngôi nhà.

Nội thất phòng khách
Là khu vực trung tâm của căn hộ nên đã được thiết kế với phong cách phóng khoáng, đảm bảo tính thẩm mỹ cao cho tổng thể tòa nhà. Các kiến trúc sư đã vận dụng vật liêu hoàn thiện có độ bền, đẹp, đảm bảo đem lại sự tinh tế trong từng chi tiết và đảm bảo sự sang trọng.

Nội thất phòng bếp
Phòng bếp của các căn hộ dự án The Privia là nơi để mọi thành viên trong gia đình quây quần bên nhau sau những giờ làm việc căng thẳng. Mọi người sẽ dược trải nghiệm các bữa ăn ấm cúng. Đồ nội thất của khu bếp được bố trí hợp lý, kích thước phù hợp. Nổi bật là tông màu gỗ trầm cùng hệ thống ánh sáng khiến ngôi nhà hiện đại hơn.











Tiến độ dự án tháng 10/2023




Mức giá bán của dự án The Privia Khang Điền hiện nay chưa được chủ đầu tư đưa ra mức chính xác. Tuy nhiên, theo như dự kiến thì khoảng giá từ 48triệu/m2. Đây là mức giá khá hợp lý cho một sản phẩm tại vị trí trung tâm, tiêu chuẩn cao cấp và của Khang Điền uy tín triển khai xây dựng.
Bảng giá bán căn hộ chung cư The Privia Khang Điền tháng 11/2023
+ Căn 1PN+ (50m2) : từ 2,4tỷ - 2,6tỷ
+ Căn 2PN+1 (65m2) : từ 3,12tỷ - 3,5tỷ
+ Căn 3PN (82m2) : từ 3,95tỷ - 4,3tỷ
Chính sách bán hàng dự kiến như sau :

THE STANDARD BÌNH DƯƠNG
The Standard là dự án tái định nghĩa tiêu chuẩn phát triển đô thị của An Gia tại các vùng dân cư hiện hữu thuộc các khu vực lân cận TP.HCM là một tiêu chuẩn sống mới cho cư dân trong tương lai. Không chỉ để ở mà còn là trải nghiệm sống đẳng cấp 5 sao
Nhà phố The Standard là dự án của An Gia Group, tọa lạc tại phường Tân Phước Khánh, Thị xã Tân Uyên, Bình Dương.
Dự án The Standard có quy mô 6,9 ha, gồm 374 sản phẩm nhà liền kề và shophouse dân số dự kiến khoảng 1.500 người. Tổng mức đầu tư cho dự án The Standard là 1200 tỉ đồng và sẽ hoàn thành đi vào hoạt động vào quý I-II/2023.
Hiện tại pháp lý dự án đã đầy đủ, hạ tầng hoàn thiện,anh chị có thể mua ở hoặc đầu tư kinh doanh..
Chỉ từ 5.3 tỷ để sở hữu căn nhà phố Standard 1 TRỆT 2 LẦU với thiết kế thông minh lệch tầng

The Standard được định vị là khu biệt lập đẳng cấp hàng đầu Bình Dương, The Standard Bình Dương mang đến những chuẩn mực sống khác biệt dựa trên triết lý 3W của tập đoàn An Gia trong thiết kế và thi công dự án
Wealthy : kiến tạo cộng đồng thịnh vượng, khẳng định - nâng tầm đẳng cấp trong phong cách sống của các chủ nhân
Wellbeing : chốn đi về ngập tràn thiên nhiên đánh thức các giác quan, nuôi dưỡng cơ thể và tâm hồn con người
Wisdom : không gian sống lý tưởng ươm mầm cho những ý tưởng sáng tạo và là lựa chọn đầu tư thông minh

Theo thông tin của Sở Xây Dựng tỉnh Bình Dương, 600 hecta dự án Trung Tâm Hành Chính mở rộng Bắc Tân Uyên được triển khai bằng nguồn vốn ngân sách và xã hội hóa nên chắc chắn Bắc Tân Uyên sẽ mời một nhà đầu tư lớn về làm dự án này. Tính đến đầu năm 2020, Bắc Tân Uyên đã hoàn thiện đúng tiến độ thi công hạ tầng cơ bản 51 hecta Trung Tâm Hành Chính Tập Trung bằng nguồn vốn ngân sách và đã tìm được nhà đầu tư về thực hiện nốt phần còn lại, do vậy mới có thông tin Vingroup về làm dự án 600 hecta ngay hồ Đá Bàn.
Sở hữu vị thế vàng “trung tâm của trung tâm”, The Standard Bình Dương tọa lạc ngay đường Hữu Khoa Huân, Bình Dương. Đây là khu dân cư hiện hữu nằm giữa các khu công nghiệp lớn như VSIP, Sóng Thần, KCN Nam Tân Uyên,…và tâm điểm của 4 thành phố: Biên Hòa - Dĩ An - Thuận An - Thủ Dầu Một
Từ The Standard Bình Dương, cư dân không chỉ dễ dàng di chuyển đến nơi làm việc mà còn có thể nhanh chóng tiếp cận hệ thống tiện ích ngoại khu bao gồm trường học, bệnh viện, trung tâm thương mại,…hay thành phố mới Bình Dương.

+5 phút đến: Khu du lịch Hồ Nam, Trường tiểu học Tân Phước Khánh B, Trường THCS Tân Phước Khánh, Chợ Vị Hảo, Chợ Tân Phước Khánh, UBND phường Tân Phước Khánh
+15 phút đến: Thành phố Thủ Dầu Một, TP.Biên Hòa , TTTM Aeon Mall Bình Dương, KCN Nam Tân Uyên, KCN VSIP 1, Khu Trung tâm thương mại & Căn hộ cao cấp Bình Dương - Astral City.
+30 phút đến : Trung tâm TP Biên Hòa, TP HCM
+50 phút : di chuyển đến Q.Bình Thạnh, Làng ĐH TP.HCM, Sân bay Tân Sân Nhất, Bến xe Miền Đông.
+Tiện ích CLUBHOUSE tầng 1
phút đến : TP Đồng Xoài, Bình Phước
Nhờ vị trí đắc địa The Standard BD được thừa hưởng tất cả những tiện ích của cả 2 trung tâm kinh tế lớn là Bình Dương và TP. Hồ Chí Minh thông qua các tuyến đường DT743, quốc lộ 1K, đường cao tốc Mỹ Phước – Tân Vạn, tuyến Metro số 1.
The Standard – khu biệt lập đẳng cấp hàng đầu tại Bình Dương, tái định nghĩa tiêu chuẩn sống:
– Vị thế vàng “trung tâm của 4 thành phố”
– Clubhouse phong cách resort
– Công viên trung tâm rộng 4.000 m²
– Không gian sống an ninh, an toàn, an lành
– Hệ thống quản gia All in one, tiêu chuẩn Nhật BảTiện ích nhà phố The Standard được chủ đầu tư chăm chút và trang bị đầy đủ các loại tiện ích sang trọng đảm bảo cho cuộc sống của cư dân nhận được sự tiện nghi nhất cũng như đẳng cấp với các tiêu chuẩn quốc tế như: Công viên nội khung với diện tích cây xanh rộng lớn, khu phức hợp thể thao, phòng Gym, Spa, Yoga hiện đại, Trung tâm thượng mại… nhằm cạnh tranh cũng như thể hiện chỗ đứng với các dự án khác tại Bình Dương.






Đáp ứng đúng thị hiếu của thị trường, KHU BIỆT LẬP PHONG CÁCH RESORT HÀNG ĐẦU BÌNH DƯƠNG – THE STANDARD đã trở thành “chốn về” trú ẩn an toàn cho sức khỏe thể chất và tài chính được nhiều khách hàng săn đón sau đại dịch.
Mô hình khu biệt lập tách biệt hoàn toàn với bên ngoài, đảm bảo an toàn cho cư dân
*Tiện ích nội khu đáp ứng đủ đầy nhu cầu sống
*Sản phẩm nhà liền thổ đảm bảo giá trị tài sản lâu bền, là kênh trú ẩn an toàn cho dòng tiền của chủ nhân.

Diện tích công viên 4,171.44 m2, diện tích Clubhouse 1,214.24 m2, diện tích cổng chào cảnh quan 191,3 m2. Tổng diện tích cảnh quan dự án là 5,576.98 m2
*Khu công viên gồm những tiện ích:
*Khu vực trẻ em: 261 m2 – Khu vực người lớn: 494 m2
*Khu vui chơi trẻ em ngoài trời: 158 m2 + Hồ bơi ngoài trời: 330 m2
*Khu vui chơi dưới nước: 103 m2 + Hồ bơi Jacuzzi: 30 m2
*Khu vực BBQ ngoài trời có mái che: 75 m2
*Khu tắm tráng: 9 m2
*Mái che pavilion (khu bãi cỏ): 50 m2
*Hồ bơi có hệ thống lọc tự động, hệ thống bồn sục Jacuzzi, đánh dấu mực nước hồ bơi theo tiêu chuẩn quốc tế và có bảo vệ hồ bơi trá
nh các tai nạn



The Standard – khu biệt lập đẳng cấp hàng đầu tại Bình Dương, tái định nghĩa tiêu chuẩn sống:
– Vị thế vàng “trung tâm của 4 thành phố”
– Clubhouse phong cách resort
– Công viên trung tâm rộng 4.000 m²
– Không gian sống an ninh, an toàn, an lành
– Hệ thống quản gia All in one, tiêu chuẩn Nhật Bả


Tiện ích CLUBHOUSE tầng 2
Với diện tích 6.9 ha không phải quỹ đất có quy mô lớn để phát triển những dự án hoành tráng về số lượng, nhưng cũng vừa đủ để An Gia triển khai thiết kế tinh túy nhất để kiến tạo không gian sống thượng lưu phục vụ các cư dân thành đạt.
ELYSIAN THỦ ĐỨC
Từ những ngày đầu, Gamuda Land đã đặt nặng yếu tố tôn trọng môi trường tự nhiên, gắn kết con người lại gần nhau hơn và tạo dựng cộng đồng văn minh, nhằm tạo ra những tác động tích cực cho đất nước mà chúng tôi đặt chân đến. Đó chính là nền tảng giúp Gamuda hiện thực hoá khát vọng và vươn xa mà họ luôn giữ vững. Dự án cải tạo Công viên Yên Sở, nằm ở cửa ngõ phía nam Hà Nội, được Gamuda Land giới thiệu như lời chào đầu tiên đến đất nước hình chữ S, biến vùng đất hoang hoá và ô nhiễm thành công viên đô thị xanh tươi, được ví như lá phổi của Thủ đô. Ngoài ra, Gamuda Land còn gắn liền với hai khu đô thị nổi bật tại hai đầu Bắc-Nam: Gamuda City quy mô 274ha tại quận Hoàng Mai, Hà Nội và Celadon City diện tích 82ha tại quận Tân Phú, Thành phố Hồ Chí Minh, cách sân bay Quốc tế Tân Sơn Nhất chỉ 5km
Lấy cảm hứng từ hình ảnh khu rừng nguyên sinh với vẻ đẹp tự nhiên được khắc họa trong sự đa dạng sinh thái, nơi trú ngụ của muôn loài, nơi có sự chuyển động không ngừng của tự nhiên được tạo hóa sắp xếp hài hòa. Một nơi có không gian sống đầy thi vị và lôi cuốn , không đơn thuần là tĩnh lặng mà còn là sự bình yên giữa cuộc sống hiện nay
Căn hộ Elysian được Land Sculptor thiết kế như một khu Rừng nhiệt đới, nơi lối sống hoà mình vào thiên nhiên xanh mát và hệ sinh thái tiện ích nội khu dự án lấy cảm hứng từ sự kết hợp của cây xanh, nước và bầu trời mang đến những trải nghiệm đầy màu sắc, thách thức mọi giác quan

| Địa Chỉ | Mặt tiền Số 170 Đường Lò Lu, phường Trường Thạnh, TP. Thủ Đức (Quận 9 cũ), TP.HCM |
| Quy Mô | 4 Block cao 20 tầng với 1406 căn hộ |
| Diện Tích | 36m2 - 115m2 |
| Loại Căn | 1 - 2 - 3 Phòng Ngủ , Penthouse , Shophouse |
| Chủ Đầu Tư | Gamuda Land |
| Đơn Vị Xây Dựng | Công ty Cổ Phần Xây Dựng CENTRAL |
| Đơn Vị Phân Phối | VietNam Property (Gamuda land) |
| Thời Gian Bàn Giao | Quý IV/2025 |
Dự án Elysian tọa lạc tại mặt tiền đường Lò Lu, phường Trường Thạnh, thành phố Thủ Đức, Elysian sở hữu vị thế vô cùng hấp dẫn, có tiềm năng tăng trưởng cao. Nằm giữa Khu Công Nghệ cao 1 TPHCM đang hoạt động và Khu Công Nghệ cao 2 sắp hình thành. Đường Lò Lu là con đường xuyên tâm kết nối trực tiếp các tuyến hạ tầng giao thông trọng điểm như Xa Lộ Hà Nội, Quốc lộ 1A, vành đài 3 và tuyến ga Metro số 1 Bến Thành - Suối Tiên
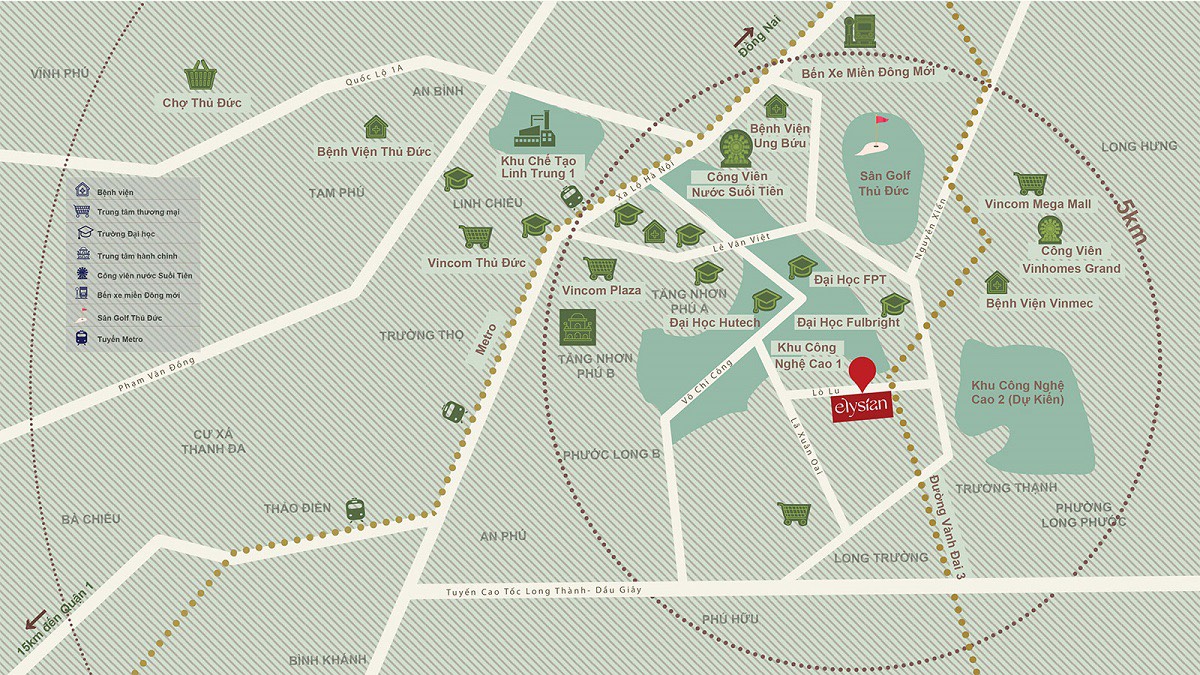
TIỀM NĂNG HẠ TẦNG KHU VỰC ELYSIAN THỦ ĐỨC
Dự án Elysian Thủ Đức kề cận khu công nghệ cao, nơi tọa lạc trụ sở, nhà máy, khu công nghiệp của nhiều của nhiều thương hiệu như Sam Sung, FPT, Thế Giơi Di Động,…Khu vực này có lợi thế dễ kết nối trung tâm hành chính thành phố Thủ Đức, di chuyển dàng đến các khu vực làng Đại học, khu Đông Sài Gòn, khu đô thị cảng Cát Lái, các quận Bình Thạnh, Quận 2 cũ, quận 7,…
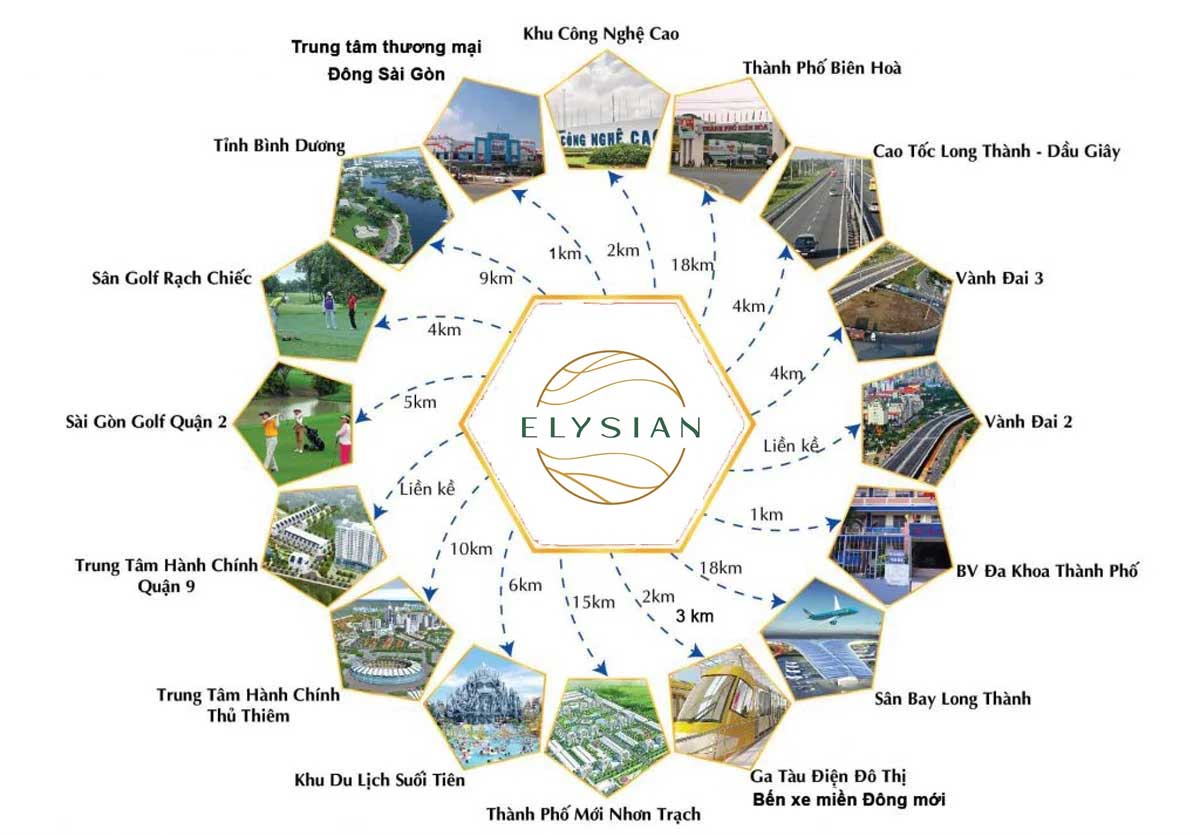
Trong tương lai cư cân của Elysian có thể tận hưởng tất cả các dịch vụ du lịch, mua sắm, giải trí cũng như giáo dục tầm cỡ nhất khu vực mà không phải mất quá nhiều thời gian di chuyển, cũng như thuận lợi giao thông phục vụ cho nhu cầu công việc.
- Tòa án nhân dân Quận 9, Đường Lò Lu, Trường Thạnh, Quận 9, Thành phố Hồ Chí Minh: 1,2 km
- Vinhomes Grand Park, Nguyễn Xiển, Long Thạnh Mỹ, Quận 9, Thành phố Hồ Chí Minh: 2,3 km
- Khu đô thị mới Đông Tăng Long, Trường Thạnh, Quận 9, Thành phố Hồ Chí Minh: 2,9 km
- Nút giao đến Vành Đai 3 và Cao tốc TP HCM – Long Thành – Dầu Giây: 4 km
- Khu Công Nghệ Cao Tăng Nhơn Phú B, Quận 9, Thành phố Hồ Chí Minh: 3 km
NGOẠI KHU
Tiện ích ngoại khu của Elysian quận 9 rất thuận tiện, trong khoản 15 phút di chuyển tới các địa điểm như: Chợ Trường Thạnh, chợ Long Trường, siêu thị Co.opmart, Vincom Thủ Đức, bệnh viện Quận 9, bệnh viện Ung Bướu, trường đại học Quốc Tế Fulbright và nhiều địa điểm khác.
Ngoài ra, dự án Elysian còn gần các khu vui chơi giải trí như: khu BCR, khu du lịch Suối Tiên, trung tâm TDTT Quận 9, sân golf Thủ Đức và nhiều địa điểm giải trí khác.
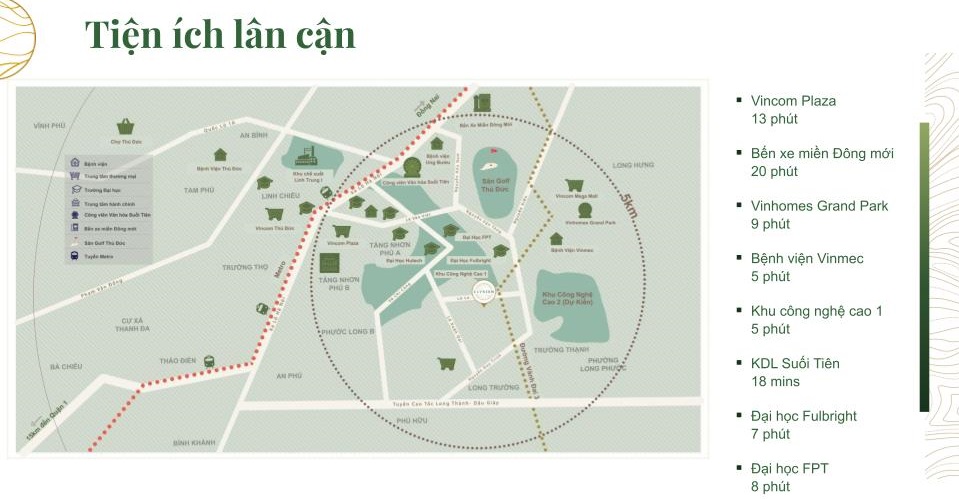
NỘI KHU
Dự án Căn hộ Elysian Lò Lu Quận 9 Thủ Đức tầng trệt nội khu là một khu rừng nguyên sinh với 350 cây xanh thân gỗ trải đều khắp dự án. Tuy nhiên, điểm nhấn chính của khu vực này là hồ bơi ngoài trời chuẩn Olympic dài 50m, và có tổng diện tích gần 1000m2 bao gồm cả hồ bơi người lớn và trẻ em. Ngoài ra, khu vực còn có sân chơi thiếu nhi rộng 280 m² và khu tiệc nướng BBQ ngoài trời. Dự án cũng có nhiều không gian xanh khác, kết hợp với các khu sinh hoạt cộng đồng như:Khu nhà hàng, Spa, Gym và vườn thư giãn, tạo nên môi trường sống đa hoạt động và kết nối cộng đồng Elysian.
Lấy cảm hứng từ các tầng sinh học của rừng, không chỉ tập trung vào cây xanh ở tầng trệt và tầng thượng, dự án Elysian còn đưa thiên nhiên len lỏi vào ban công vào các tầng giữa, tạo nên một mặt tiền xanh đột phá. Thiết kế này kết nối cuộc sống hằng ngày của cư dân chạm gần hơn với thiên nhiên, bền bỉ với thời gian và nhưng giá trị bất biến.
Chủ đầu tư Gamuda Land cam kết xây dựng Elysian với thiết kế đặc trưng độc đáo, tập trung chính vào bảo vệ toàn diện không gian sống hòa quyện với thiên nhiên và đa dạng sinh học. Công ty sẽ không ngừng cải tiến sản phẩm để nâng cao chất lượng các dự án thiết kế xanh cho các dự án ra mắt sắp tới. Trong tương lai gần, khách hàng sẽ thấy nhiều dự án mang phong cách Biophilic của Gamuda Land, với sự quy hoạch tổng thể để tạo ra nhiều “rừng trong phố” hơn và trồng cây nhiều hơn. Tất cả các sản phẩm của Gamuda Land sẽ được thiết kế theo tiêu chuẩn xanh và đảm bảo tiêu chí tiết kiệm năng lượng hơn so với các dự án khác trên thị trường.
Kết nối với thiên nhiên thông qua tầm nhìn thị giác. Kết nối với thiên nhiên thông qua các giác quan khác, khứu giác và thính giác… Sự thay đổi nhiệt độ và lưu thông không khí trong căn hộ. Một căn hộ biết thở là hướng đến việc tạo nên môi trường sống lành mạnh và hiệu quả đối với con người – nơi thiên nhiên và công nghệ được kết hợp một cách hài hòa.
Dự án Elysian của Gamuda Land được thiết kế cảnh quan bởi Land Sculptor với phong cách Biophilic, tạo sự kết nối giữa con người và thiên nhiên là trọng tâm. Trong khuôn viên dự án, có khu vực bể bơi trung tâm chuẩn Olympic kích thước 10m x 50m, cùng với các hồ bơi cho trẻ em và khu sục Jacuzzi được bố trí để tạo không gian rộng rãi cho cư dân thư giãn tận hưởng những ngày cuối tuần tại gia như 1 khu resort cao cấp.

Pocket Sky Garden nằm rải rác khắp các tầng ở tòa nhà, mở rộng khái niệm xanh theo chiều thẳng đứng, đồng thời đóng vai trò là lá chắn thực vật giúp thanh lọc không khí, bụi bẩn, hấp thụ nhiệt và giảm tốc độ gió từ đối lưu không khí. Pocket Sky Garden sẽ mang lại bầu không khí trong lành cho những ai muốn thư giãn và hòa mình vào không gian ngoài trời

Toàn bộ căn hộ Elysian Lò Lu đều có thiết kế vuông vức, bố trí thông minh, hài hòa nhằm phát huy tối đa công năng sử dụng diện tích. Hệ thống cửa sổ kính lắp đặt khoa học, tận dụng ánh sáng và gió tự nhiên, mang lại nguồn sinh khí dồi dào cho từng căn hộ. Nhờ đó, không gian sống của cư dân dự án Elysian Gamuda cũng trở nên thông thoáng và khỏe mạnh, thoải mái hơn.



Thiết kế căn hộ được tính toán hợp ý và khoa học căn hộ Elysian sẽ đáp ứng đầy đủ nhu cầu của từng nhóm khách hàng khác nhau, và tận dụng tối đa từng m2 công năng trong ngôi nhà của bạn, không có không gian thừa. Với diện tích đa dạng từ 34 – 115 m2, đầy đủ loại như căn Studio, 1PN, 1PN+1, 2PN, 3PN, Shophouse,…






ELYSIAN THỦ ĐỨC NỔI BẬT VỚI NHỮNG ƯU ĐIỂM


THE MAISON BÌNH DƯƠNG
TỔNG QUAN
Địa Chỉ
Đường Phan Bội Châu, Phú Thọ, Thành phố Thủ Dầu Một, Bình Dương
Quy mô 2 Block cao 29 tầng với 632 căn hộ
Diện tích 46m2 - 70m2 - 75m2 - 78m2 - 83m2
Loại căn 1 - 2 - 3 Phòng Ngủ
Chủ đầu tư C-Holding
Đơn vị xây dựng Công ty Cổ Phần Đầu Tư Phát Triển Xây Dựng C-Contructions
Đơn vị phân phối Nguyên Lâm (C-Holding)
Thời gian bàn giao Quý IV/2024
BẤT ĐỘNG SẢN 247
Chúng tôi đã giúp hàng nghìn khách hàng tìm được căn hộ ưng ý. Với quỹ hàng đa dạng nhất thị trường,chúng tôi tự tin sẽ giúp bạn thực hiện giấc mơ sơ hữu BĐS và tối ưu hiệu quả đầu tư.
Dự Án Đã Hoàn Thiện
Đối tác
Tìm kiếm sản phẩm
Danh mục sản phẩm
 |
THE WORKSHOPLocal customers are welcome to pick up their orders during our regular hours. Other visits by appointment only. Please contact us to set up a visit.
COMPANY:CTY CP ĐT & PT BẤT ĐỘNG SẢN AN GIA
ADDRESS:63A Nam Kỳ Khởi Nghĩa, Phường Bến Thành, Quận 1, TP.HCM
HOTLINE:0819 020 689
|



























